Les sténopés n'ont pas de cercle d'image,
seulement des cercles de confusion
La pratique
par Paul Kopff
Calculez à présent
les performances de votre stenopé
calculateur pour sténopé
classique
calculateur pour sténopé
anamorphique
Introduction
Il est bien connu que les objectifs équipant les
appareils photographiques concentrent la lumière d'un paysage (par
exemple) qui les pénètre en un plan à une certaine distance appelée
la focale.
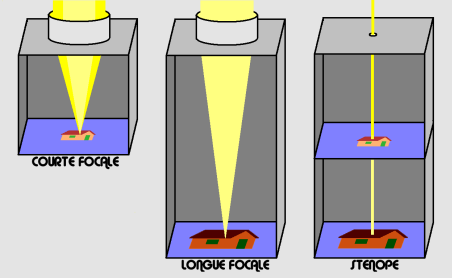
Dans cette figure, deux objectifs l'un de
“courte” focale et l'autre de “longue” focale (par exemple de deux
fois la focale du premier) ont le même diamètre d'ouverture et
laissent donc entrer la même quantité de lumière. L'objectif de
longue focale qui fait converger la lumière deux fois plus loin
projette une image deux fois plus grande suivant ses deux dimensions
et cette image ayant quatre fois la superficie de celle projetée par
la courte focale est quatre fois moins lumineuse et nécessite donc
un temps de pose quatre fois plus long pour impressionner la même
pellicule.
Si avec la courte focale on veut une image pas
plus lumineuse qu'avec la longue focale (pour avoir le même temps de
pose), il faut “diaphragmer” c'est a dire réduire de moitié le
diamètre par lequel l'objectif de courte focale laisse entrer la
lumière.
Pour que les posemètres n'aient pas de problèmes
avec les focales, on a convenu d'une échelle de nombres d'ouverture
équivalents pour toutes les focales, qui représentent le rapport de
la focale au diamètre de l'ouverture laissant pénétrer la lumière.
Et cette échelle est une progression bien connue de facteur (en gros)
1,4 soit : [1 – 1,4 – 2 – 2,8 – 4 – 5,6 – 8 – 11 – 16 – 22 – etc.].
Ainsi, quelle que soit la focale, quand on passe d'un nombre
d'ouverture de cette progression au voisin, il faut pour compenser
l'exposition soit multiplier soit diviser sa durée par 2. D'où la
progression bien connue des temps de pose en fractions de seconde :
[ 1 – 2 – 4 – 8 – 15 – 30 – 60 – 125 – 250 – 500 – etc.].
Un sténopé n'est pas un objectif photographique,
juste un trou minuscule, qui laisse pénétrer un très fin faisceau
lumineux. Par conséquent, il ne focalise pas l'image en un plan
déterminé, on peut placer la pellicule où on veut. Plus on la place
loin du sténopé, plus l'image sera grande dans ses deux dimensions :
si par exemple on place le sténopé deux fois plus loin, l'image sera
deux fois plus grande dans ses deux dimensions, donc quatre fois
plus grande en superficie, et donc quatre fois moins lumineuse : on
peut définir le nombre d'ouverture d'un sténopé tout comme ceux d'un
objectif photographique, comme le rapport entre sa distance à la
pellicule qui lui fait face et son diamètre.
Les posemètres s'y retrouvent exactement comme
s'ils avaient affaire à des objectifs ! Mais bien entendu, le nombre
d'ouverture qui représente le diaphragme d'un sténopé est beaucoup
plus grand que ceux de la gamme qu'on trouve habituellement sur les
objectifs photographiques, et les temps de pose doivent donc être
beaucoup plus longs : selon le cas, déjà quelques secondes en plein
soleil, alors qu'avec un objectif photographique fermé à 16 on est
au 1/125 (à 125 iso, d'après la règle f/16).
Certains passionnés de sténopés ont fabriqué des
appareils “super-grand-angle” ou panoramiques, c'est à dire des
appareils contenant des pellicules de dimensions beaucoup plus
grandes que la “focale” du sténopé (sa distance au centre de l'image).
Utilisant ces appareils, ils ont fait l'expérience de
l'assombrissement progressif de l'image quand on s'éloigne de son
centre. On appelle ce phénomène "vignettage", par analogie à un
défaut plus ou moins marqué qui affecte aussi les objectifs
photographiques, quand ils projettent des images pas tout à fait
uniformément lumineuses sur toute la surface sensible. Les appareils
à sténopé vignettent donc, et ça se remarque surtout aux très grands
angles car c'est très progressivement ; mais au contraire des
optiques photo qui peuvent le corriger plus ou moins à l'intérieur
d'un cercle appelé "le cercle d'image" (couvrant le format pour
lequel ils sont prévus : 24x36, 6x6, etc.), pour les sténopés, il
n'y a pas de remède.
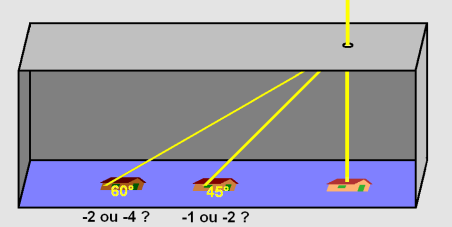
Un jour sur le forum favori des sténopistes (F295
– en anglais !), il y a eu débat à propos de ce vignettage. Certains
proposaient l'explication simple suivante : comme avec l'inclinaison
des faisceaux lumineux la distance entre le sténopé et la pellicule
augmente, c'est comme si la focale variait. Mais si l'on s'en tient
à cette explication, on devrait trouver qu'à 45°, comme la focale a
été multipliée par 1,4 pour un diamètre inchangé, l'image est
assombrie comme si on avait fermé d'un diaphragme. Et à 60°, la
focale étant multipliée par 2, on perdrait 2 diaphragmes.
Il y a eu débat, car certains autres croyaient
savoir qu'on perdait deux diaphragmes dès 45°, et quatre diaphragmes
à 60°. Pour apporter des arguments à cette discussion, j'ai élaboré
un modèle physique qui retrouve le résultat connu, car il prend
aussi en compte le fait que les faisceaux lumineux inclinés sont
“pincés” par l'ovalisation de la surface apparente du sténopé.
Ce phénomène, quand il a été reconnu, a aussi
alimenté une autre discussion à propos des
appareils “anamorphiques”. Dans ce type d'appareils, il se
trouve que la distance du sténopé à la pellicule est la plus courte
pour les angles les plus rasants où l'ovalisation est la plus
flagrante.
La question soulevée était : dans quelle mesure
ces deux phénomènes (l'ovalisation et la variation de la distance
entre le sténopé et la pellicule) se contre-balancent-ils ? Ce qui
m'a motivé pour élaborer un autre modèle pour ce type d'appareil. On
trouve effectivement que le vignettage y est plus contenu (sans pour
autant qu'il soit éliminé – ne rêvons pas !).
Ensuite, sur une si bonne voie, je me suis
intéressé aussi à un autre phénomène caractéristique des appareils à
sténopé super-grand-angle : l'image a tendance à devenir de plus en
plus floue quand on s'éloigne de son centre ; j'ai donc ajouté à mes
modèles des évaluations des cercles de confusion et des taches de
diffraction aux incidences très rasantes.
Et entre temps, j'y avais ajouté l'influence de
l'épaisseur du sténopé, qui ne peut pas être considérée comme
négligeable dans tous les cas de figures.
J'avais plein de
jolies formules
mathématiques (mais elles n'étaient jolies que pour moi – et
d'autres fadas du même acabit). Pour en faire quelque chose d'utile
à tous, je me suis mis alors à développer de petits programmes (en
javascript) implémentant ces formules et qui permettent de jouer
avec tous les paramètres (la “focale”, le diamètre et l'épaisseur du
sténopé, etc.) en manipulant des réglettes à curseurs et de voir
leur influence sur des courbes d'assombrissement et de confusions
qui “bougent” pratiquement en temps réel.
Ces outils de simulation sont mis en ligne
pour la première fois ici !
mais pour ceux que ça intéresse, les modèles
qu'ils implémentent sont détaillés
là-bas...
Cercle d'image, cercles de confusion : mode
d'emploi
Quand on veut se
construire un appareil photographique à sténopé, la première
décision qu'on prend concerne la perspective qu'on recherche :
l'angle de prise de vue, qui est déterminée par la taille de l'image
et la distance du sténopé à la surface sensible.
Cela étant posé, on peut déterminer le diamètre
optimal du sténopé, et en général, on le fait grâce à la formule
simple qu'utilisent tous les “calculateurs” visibles ailleurs sur le
web” :
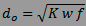
Etant bien entendu que cette formule n'optimise
le diamètre du sténopé que dans l'axe d'un appareil “classique” !
Pour aborder le problème du “piqué” des appareils
à sténopé et de leur “vignettage” en considérant dans les deux cas
traités (les “classiques” et les “anamorphiques”) toute la surface
sensible, mes deux outils montrent des courbes fonctions de la
position x d'un point quelconque de la pellicule.
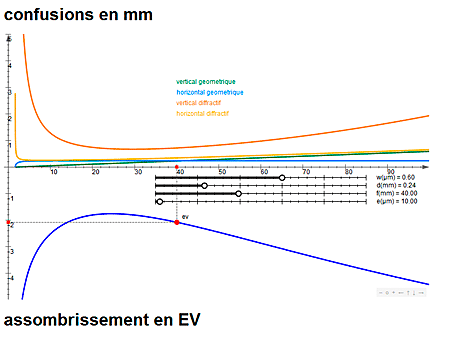
Au dessus de l'axe horizontal des x, il y a
quatre courbes de couleurs différentes montrant comment varient en
fonction de x les dimensions radiales et tangentielles des taches de
confusion géométriques et diffractives. En dessous de l'axe, une
courbe unique montre en fonction de x comment l'image s'assombrit.
Les quatres courbes des “confusions” sont repérés suivant un axe
vertical gradué en mm (millimètres) et l'axe vertical de la courbe
de “vignettage” l'est en EV (exposure value, ou – en français – IL
: indice de lumination – ou plus familièrement : “diaph's”).
On peut dans chaque outil changer les valeurs de
quatre paramètres de dimensionnement et observer pratiquement en
temps réel leur influence sur les cinq courbes de la simulation.
Ceci se fait avec quatre réglettes manipulables par la souris. Le
diamètre d du sténopé (en mm), l'épaisseur e de la membrane dans
laquelle il est percé (en microns) et la longueur d'onde w de la
lumière (en microns) ont la même signification dans les deux outils
(savoir que 0,6µm est le jaune/vert au milieu du spectre visible ;
0,4µm est le violet et 0,8µm le rouge à ses deux extrémités).
Mais de même que x, le paramètre f dimensionnant
la “camera obscura” a une signification différente suivant les deux
cas :
1/ Outil de
simulation des appareils à sténopé classiques
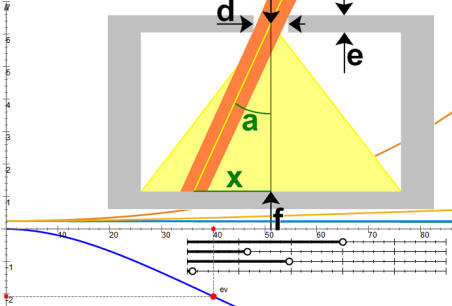
Pour ouvrir cet outil cliquez sur cette image qui rappelle les
paramètres significatifs de la simulation
Pour cet outil, x représente sur la surface du
film la distance (en mm) d'un point dans n'importe quelle direction
par rapport au “centre” de l'image, qui est le point du film à la
perpendiculaire du sténopé. Et la “focale” f (en mm) est la
distance entre ce point “centre” de l'image et le sténopé.
La courbe dans la moitié inférieure du graphe (en
bleu foncé) donne en fonction de x (en mm) l'assombrissement en EV (ou
en IL ou en diaph's, comme vous préférez l'appeler). Au centre,
l'image n'est pas assombrie par rapport au “diaph” théorique f/d. On
voit notamment qu'à une distance x égale à la focale f (c'est à dire
: à 45° d'incidence) on a -2ev ; on perd donc 2 “diaph's” par
rapport au centre. A des distances supérieures, le vignettage
devient notable : on passe dans le domaine des appareils à sténopé
“ultra-grand-angulaires” et il vaut mieux bien choisir ses sujets et
cadrages pour atténuer la visibilité de cet effet (ou à dessein,
l'exagérer ?).
La moitié supérieure du graphe contient quatre
courbes fonctions de x, qui donnent les dimensions (en mm) des
taches de confusion “géométriques” et “diffractives” dans deux
directions perpendiculaires : “radial” veut dire en s'éloignant du
“centre” et “tangentiel”, perpendiculairement – sur le cercle des
points à la même distance du “centre” . En réalité, les deux
phénomènes ne peuvent être isolés et il faut voir dans la
distinction “géométrique/diffractive” une estimation de leurs
influences relatives, un point c'est tout.
Au centre de l'image, c'est à dire à x=0 : si le
sténopé est “optimisé”, les dimensions “géométriques” et
“diffractives” sont égales. Mais si l'on s'éloigne du centre de
l'image, les dimensions “diffractives” croissent, surtout la “radiale”.
C'est ce qui explique l'effet de “coup de zoom” notable sur les
images faites avec des appareils à sténopé “ultra-grand-angulaires”
(effet similaire à celui d'un coup de zoom pendant l'exposition –
c'était un truc à la mode, il fut un temps).
Quand on change le diamètre du sténopé, on peut
voir les quatre courbes se séparer à x=0, mais peut-être rester un
peu mieux groupées un peu plus loin (du centre aux coins de l'image,
ce qui nous intéresse donc : tous les x inférieurs à sa
demi-diagonale). La plupart des sténopistes se contente d'optimiser
“au centre” et les amateurs de sténopés “grand-angle” apprécient
même souvent l'effet combiné d'un vignettage important et du “coup
de zoom”.
2/ Outil de
simulation des appareils à sténopé anamorphiques
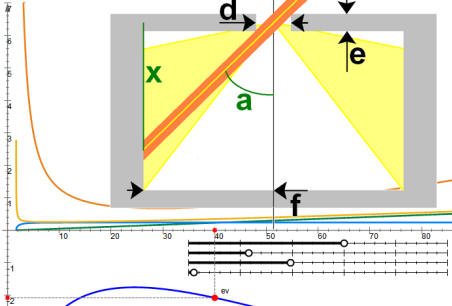
Pour ouvrir cet outil cliquez sur cette image qui rappelle les
paramètres significatifs de la simulation
Parmi ces appareils, on considérera les plus
courants : ceux où le film est déroulé à l'intérieur d'un cylindre
de rayon f (en mm) et le sténopé est percé au centre de son “couvercle”.
Pour ce deuxième outil de simulation, x (en mm) est la distance
“normale” d'un point de la pellicule au couvercle.
La courbe dans la moitié inférieure du graphe (en
bleu foncé) donne en fonction de x (en mm) l'assombrissement en EV (ou
en IL ou en diaph's, comme vous préférez l'appeler). Il est
difficile de déterminer un point de référence objectif pour cet
assombrissement, car en face du sténopé, il n'y a pas de pellicule.
Par convention, on prendra un point de référence en face du sténopé
à la distance f, afin que le vignettage puisse être comparé à celui
d'un appareil classique.
On note alors que par rapport à ce point de
référence, où le diaphragme vaut en principe f/d, la courbe
d'assombrissement reste toujours en-dessous, de plus de 1,5 diaph's
! Intrinsèquement, ayant choisi le diamètre f du cylindre et le
diamètre d du sténopé, il faut tenir compte de ce décalage. Mais on
peut aussi noter qu'à l'incidence 45° on a toujours -2ev, et que le
vignettage de ces appareils semble mieux contenu que celui des
appareils grand-angle classiques (du moins du côté des x croissants,
de l'autre côté, quand x s'approche de 0, l'image s'assombrit très
vite).
La moitié supérieure du graphe contient quatre
courbes fonctions de x, qui donnent les dimensions (en mm) des
taches de confusion “géométriques” et “diffractives” dans deux
directions perpendiculaires : “vertical” veut dire suivant les
“génératrices” du cylindre et “horizontal”, sur ses cercles
“directeurs” . En réalité, les deux phénomènes ne peuvent être
isolés et il faut voir dans la distinction “géométrique/diffractive”
une estimation de leurs influences relatives, un point c'est tout.
Les courbes montrent (quand on fait varier le
diamètre du sténopé) qu'on ne peut nulle part considérer une
“optimisation” possible, mais que la formule “agréée” pour les
appareils à sténopé classiques propose un compromis qui semble
acceptable : pour garder ce compromis acceptable quand on change le
diamètre f, le mieux qu'on puisse faire est d'ajuster le diamètre d
en conséquence, de façon à égaliser le “diffractif horizontal” là
où il est minimal, avec le “géométrique horizontal”.
Mais il est recommandé après cela de faire des
essais “en vrai” autour du compromis trouvé, et que chacun choisisse
la solution qui lui plaît le mieux : personnellement, je reste avec
le diamètre d suivant le compromis de la formule, qui est du côté
des plus petits choix possibles.
Calculez à présent
les performances de votre stenopé
calculateur pour sténopé
classique
calculateur pour sténopé
anamorphique
Cercle d'image,
cercles de confusion :
deux études de cas
1/ Le sténopé anamorphique POLKa
Le principe de cet appareil est décrit
là bas, et les valeurs utilisées ici sont celles de l'ExaktPOLKa.
Le cylindre qui met en forme la pellicule a un
rayon f = 35mm et la fenêtre d'exposition pour des rollfilms 120 va
de x = 8mm (incidences les plus rasantes) à x = 63mm, offrant donc à
l'image une hauteur de 55mm (sur un rollfilm 120, c'est presque le
format 6x18 classique des panoramiques). Ces limites sont marquées
sur les figures ci-dessous par deux traits épais bleu-vert.
Les deux simulations ci-dessous considèrent dans
une même membrane de e = 0,01mm (de l'alu. d'emballage par exemple)
deux diamètres de sténopé : d = 0,23mm et d = 0,32mm.
Sur les courbes d'assombrissement on constate que
dans les deux cas par rapport au maximum, du côté des incidences
rasantes on perd moins de 1ev, et de l'autre côté à peine plus de
1,5ev, ce qui constitue un vignettage somme toute modéré (qui permet
d'envisager de la diapo avec ces appareils !)
Sur les courbes des confusions, on constate que
le flou est dominé, surtout aux grands bords de l'image, par la
diffraction verticale ; mais nettement moins quand on agrandit le
sténopé en faisant passer son diamètre de 0,23mm (donné comme
optimal par les calculateurs) à 0,32mm.
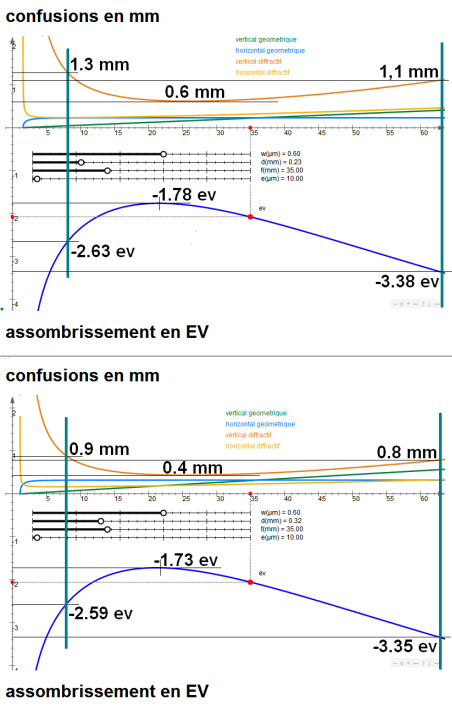
J'ai adopté sur mes POLKa des sténopés d'environ
0,25mm de diamètre car je considère que le flou perceptible aux deux
grands bords des images n'est pas subjectivement trop génant, car il
affecte principalement une seule direction (les verticales).
2/ Un classique
sténopé grand angle... mais avec un zoom.
Pour faire un appareil à sténopé muni d'un zoom,
rien de plus simple, il suffit de faire varier la distance entre le
sténopé et la pellicule, en interposant un soufflet. Le problème qui
se pose est :quand on change la focale, est-ce que le diamètre du
sténopé reste “optimal” ? Les calculateurs de sténopé optimal du web
disent que non, mais voyons cela de plus près...
Imaginons qu'on colle devant un magasin
Hasselblad (ou Kiev, la qualité suédoise n'est pas indispensable) un
soufflet et un sténopé. Le magasin permet de faire des photos 6x6,
plus exactement, il découvre une fenêtre d'image de 56x56mm. Posons
que le soufflet permet de faire varier la focale entre 17mm (très
grand angle) et 51mm (modérément grand angle). Et jouons avec notre
outil pour trouver le bon diamètre...
A la focale de 51mm, les calculateurs de sténopés
optimaux nous donnent un diamètre de 0,27mm
A la focale de 17mm, les calculateurs de sténopés
optimaux nous donnent un diamètre de 0,16mm
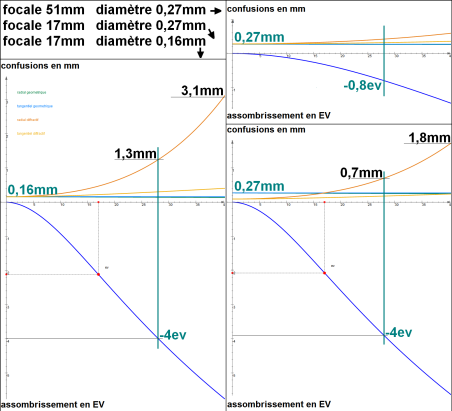
Deux diamètres "optimaux" très différents, les
optimiseurs patentés du web nous conseillent donc fermement de
changer de sténopé ! Voyons ce qu'il en est :
D'abord, notons que les bords de l'image sont à
28mm du centre et les coins à 40mm ; on ne regarde donc les courbes
que pour x compris entre 0 et 40mm, et j'ai aussi tracé sur les
courbes des traits verticaux à 28mm pour marquer les bords de
l'image.
J'ai fait tourner mon outil pour regarder ce qui
se passait à la focale de 51mm pour le trou de 0,27mm. La résolution
au centre est de l'ordre de 0,27mm pour les quatre confusions (ce
qui est normal, puisque ce diamètre est optimal pour cette focale).
Elle ne se dégrade pas sensiblement, et même dans les coins, seul le
flou de diffraction radial a doublé. Le vignettage aux bords est de
-0,8ev, et dans les coins de moins de -1,5ev. C'est bien !
Ensuite, j'ai fait tourner mon outil pour
comparer ce qui se passait à la focale de 17mm, pour un trou de
0,16mm soi-disant optimal à cette focale, et le trou de tout à
l'heure de 0,27mm.
Le résultat est éloquent : Dans les deux cas, aux
bords de l'image on perd en gros 4ev et dans les coins presque 6ev,
ce qui représente un vignettage considérable ! Mais peut-être encore
maîtrisable par certaines pellicules (oubliez les diapos !). En
revanche, au niveau du piqué, grosse déception : évidemment au
centre de l'image, le trou de 0,16mm donne de meilleurs résultats (puisqu'il
est “optimal”), mais voyez combien la diffraction (surtout radiale)
dégrade la situation aux bords et dans les coins ! Si on aime, ça va,
mais si on n'aime pas, il faut bien avouer que de garder le trou de
0,27mm – optimal pour la focale de 51mm – n'est pas une si mauvaise
idée, et que même au centre, son piqué reste correct (0,27mm à la
focale de 17mm comme à celle de 51mm).
Conclusion
En plus de permettre de dimensionner à
l'avance “le sténopé idéal”, ces outils donnent à comprendre “ce qui
se passe” sur toute la surface sensible, et donc de se rendre plus
familier avec ce qu'on peut voir sur des images prises avec des
appareils à sténopé un peu extrémistes (super-grand-angle ou
anamorphique)...
La deuxième étude de cas nous laisse entrevoir
qu'il peut être tout aussi délicat de choisir le “bon” sténopé pour
un projet donné que la “bonne” optique pour son rendu dans un
appareil photo classique. En particulier, les projets d'appareils
grand-angle ne devraient pas utiliser bêtement les outils de
dimensionnement optimal qu'on trouve ici ou là ; en tous cas, pas en
se référant à la (distance du sténopé à la pellicule) soi-disant
focale !
Je proposerais plutôt une méthode qui utilise la
demi-diagonale de l'image comme point de départ.
Dans un premier projet, il faudrait essayer en
vrai plusieurs diamètres et noter pour chacun d'eux en se servant de
mon outil le rapport entre la résolution au centre de l'image et
celles aux bords aux coins. Pour le sténopé dont on préfère les
images, on mémorise ces rapports.
Par la suite – en commençant avec le sténopé
donné par la demi-diagonale – on chercherait avec mon outil à
retrouver ces mêmes rapports. Mais on peut compliquer, en donnant
aussi de l'influence au vignettage. Ou alors, on ne calcule rien, on
est là pour s'amuser...
Calculez à présent
les performances de votre stenopé
calculateur pour sténopé
classique
calculateur pour sténopé
anamorphique
Voir aussi :
“Les
sténopés n'ont pas de cercle d'image, seulement des cercles de
confusion. La théorie”
est un article jumeau qui détaille les arguments
et formules derrière ces modèles... seulement pour les très curieux
! Et d'après ce qu'on me dit... pour les très courageux ! |

