[abonnement gratuit]

l'auteur

Optimiser son sténopé :
le tour des trous en quelques abaques

par Emmanuel Bigler

Détermination du meilleur sténopé possible
pour un format de film donné.

Le choix du diamètre du sténopé dépend de la distance choisie sténopé-film. Un bon sténopé peut couvrir en diagonale un angle de 120° ce qui donne un cercle de diamètre environ égal à 3,4 fois la distance sténopé-film. En restant moins exigeant on peut néanmoins couvrir facilement 90° en hauteur sur le format de film ce qui donne une hauteur d’image raisonnable égale à deux fois la distance sténopé-film.

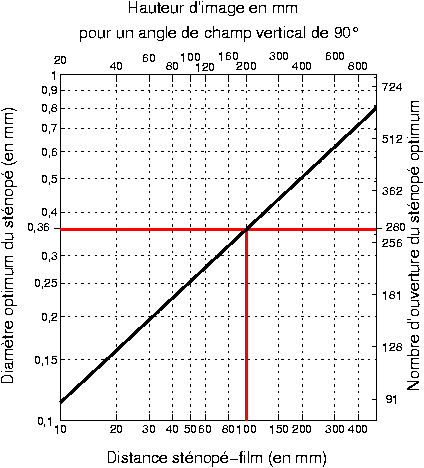
figure 1

Rappelons que la distribution de lumière dans l’image sténopé obéit à une loi de répartition de type cos⁴(θ)
ce qui conduit à une chute de luminosité énorme, de l’ordre d’un facteur 16, 4 diaphragmes, à +-60° de l’axe. Il est donc raisonnable d’en rester à +-45° en hauteur dans le roto-sténopé ce qui donne tout de même une perte d’un facteur 4, deux diaphragmes.

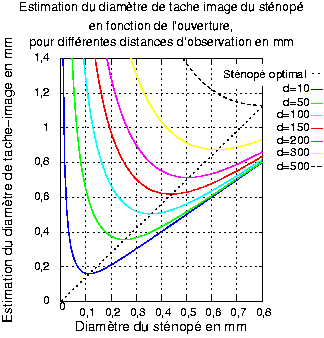
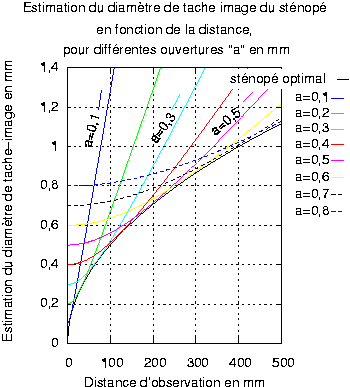
Le premier et deuxième graphiques expliquent comment choisir la dimension optimale du trou en fonction de la distance et donnent le nombre d’ouverture donc la luminosité du sténopé correspondant. En regard, on a mentionné la hauteur d’image pour 90° de couverture verticale soit deux fois la distance sténopé-film.

L’extrapolation du temps de pose requis pour un nombre d’ouverture N₂ lorsque le posemètre donne une indication pour N₁ est de multiplier par (N₂/N₁)².

Par exemple sur le sténopé de distance 100 mm optimal on a un diamètre de 0,36mm et un nombre d’ouverture de 280, la règle de seize par soleil brillant va nous suggérer 1/125 s f/16 avec du film de sensibilité ISO 125 pour une scène de plein air.
Le coefficient multiplicatif du temps de pose sera donc (280/16)² = 306.
Le temps de pose suggéré sera donc 306/125 = 2,5 secondes environ.
Pour un tel temps de pose de l’ordre de quelques secondes on pourra dans un premier temps ne pas tenir compte des effets de non-réciprocité du film.

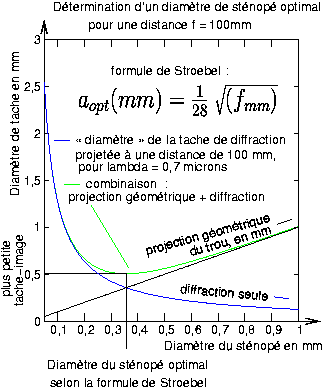
Le deuxième graphique explique pourquoi il existe un sténopé optimal. Partant d’un grand diamètre de sténopé on démarre avec une tache-image qui est simplement la projection du trou, projection quasi-parallèle lorsque l’objet est loin. Pour améliorer la qualité de l’image il est donc légitime de diminuer ce diamètre jusqu’à ce que les effets de diffraction apparaissent. La plus petite tache possible est obtenue lorsque l’effet de projection géométrique contribue à peu près autant que la diffraction à la dimension de la tache image ce qui nous donnerait pour un éclairage monochromatique une valeur 

où λ est la longueur d’onde d’éclairage.

figure 2

Pour la lumière visible entre 0,4 et 0,8 microns, on utilisera la formule empirique donnée par Stroebel : 

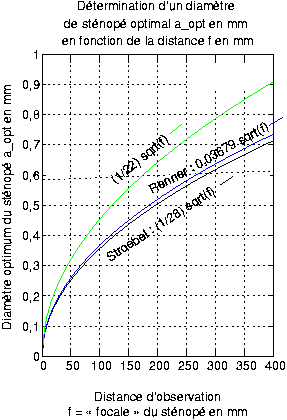
figure 3

Les figures 4 et 5 proposent une détermination approchée de la dimension de tache-image lorsqu’on fait varier soit le diamètre du sténopé soit la distance d’observation, et montrent comment le choix du sténopé optimal permet d’avoir la plus petite tache-image possible donc l’image la plus nette possible.

figure 4

figure 5

Le dernier graphique tente de quantifier le nombre de pixels équivalents dans l’image sténopé en comptant le nombre de taches supposées adjacentes qu’on peut ranger dans un format carré de diagonale 2d.

figure 6

On voit que si on a évidement tout intérêt, à format donné, à utiliser le sténopé optimal, il y a une tolérance assez peu stricte sur ce choix et de toutes façons plus le format de film couvert sera grand, meilleure sera la qualité d'image sans néanmoins espérer dépasser une valeur de l'ordre du million de taches-images adjacentes. Il est délicat de calculer un nombre de pixels équivalents ; identifier le nombre de taches adjacentes au nombre de pixels néglige le fait qu'un bon échantillonnage doit compter deux pixels par période dans les deux directions d'espace ; ici la période limite est égale au diamètre des taches adjacentes, il est donc à la fois plus raisonnable et en parfaite conformité avec les règles classiques de l'échantillonnage de multiplier finalement par quatre le nombre de taches adjacentes dans toute la surface de l'image pour obtenir un maximum de l'ordre de quelques
3 à 4 méga-pixels pour un très grand format d'image sténopé de l'ordre de 70x70 cm.

Comme le roto-sténopé procède par raccordement de champs le nombre total de pixels sera simplement la somme des contributions de toutes les bandes d’image, mais on ne prend que la partie centrale du format là où l’image est la meilleure et la plus uniformément éclairée.

Référence :
Leslie D. Stroebel, “View Camera Technique”, 7-th Ed., ISBN 0240803450, Focal Press, http://www.focalpress.com , 1999

Dernière mise à jour : 2005