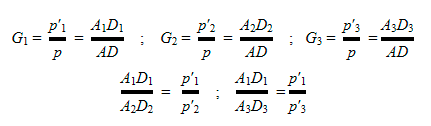|
|
||||||||||||||||||||||||||||||||||||||||||||

l'auteur
Télécharger cet article
|
Angles de champ, focales, projections
|
|||||||||||||||||||||||||||||||||||||||||||
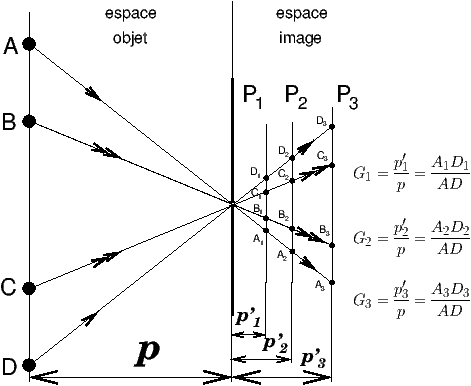
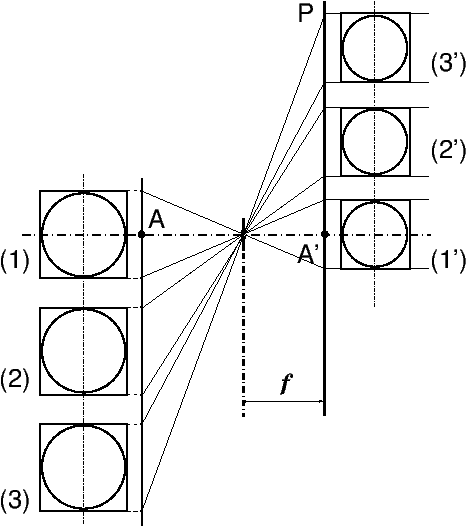
Figure 1: La camera obscura de la Renaissance
Dans une camera obscura, on peut placer le plan ou la surface de projection comme on veut, à volonté en P1, P2, ou P3, on est ramené au tracé de perspective conique classique. En éloignant le plan de projection du sténopé, les images se déduisent l’une de l’autre par un facteur de grandissement linéaire G1, G2,G3, en proportion directe de la distance entre le sténopé et le plan de projection :
|
|
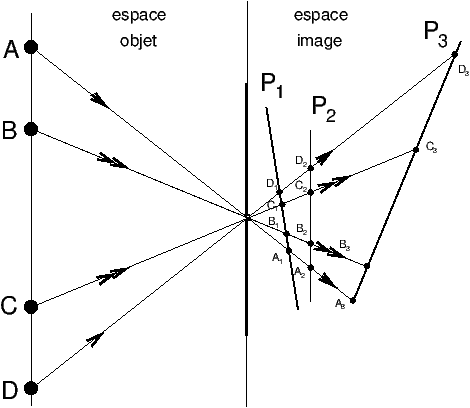
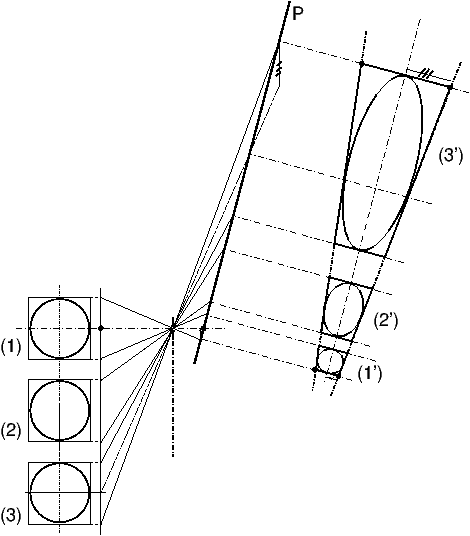
Figure 2: Camera obscura et projection sur un plan incliné : aucune condition de netteté ou de réglage de mise au point n’est requise, la projection peut se faire sur une surface arbitraire
On peut bien entendu pencher le plan de projection comme ou veut ou projeter sur n’importe quelle surface, dans l’imagerie par sténopé, il n’y a pas de condition de mise au point ou de notion de plans conjugués. Si on projette sur un plan incliné, l’image d’un carré devient un trapèze, l’image d’un cercle devient une ellipse, la belle simplicité de la projection sans distorsion entre plans parallèles disparaît, le grandissement devient variable le long du plan de projection.
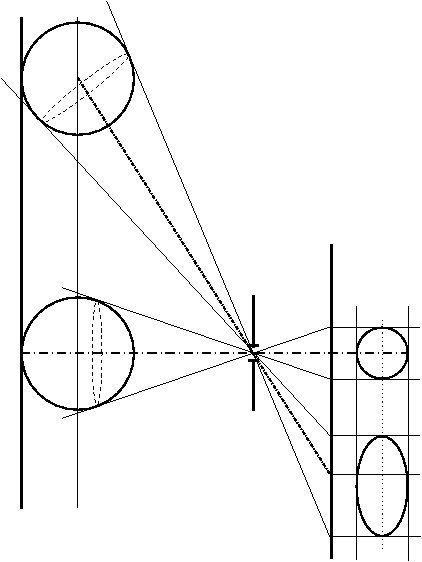
La figure (3) représente la projection d’un carré et d’un cercle inscrit dans le carré, entre plans parallèles. On notera que même si le cercle est très loin de l’axe optique AA′ (cercle N°3 sur la figure 3), la projection de ce cercle reste un cercle, bien que le cône de rayons correspondant soit très incliné.
Si le plan de projection est incliné par rapport au plan de l’objet, la projection d’un carré devient un trapèze et le cercle inscrit dans le carré devient une ellipse inscrite dans le trapèze (figure 4). Toute droite de l’objet se projette comme une droite si la surface de projection est plane; donc il n’apparaît pas de distorsion optique dans laquelle une droite se projetterait comme une courbe, un rectangle prenant la forme d’un barillet ou d’un coussinet. Bien entendu, si la projection est faite sur un cylindre ou toute autre surface non plane, on obtient une image en anamorphose, un jeu avec les formes très en vogue à la Renaissance [1].
Bien noter que dans la camera obscura l’inclinaison de la planchette portant le petit trou n’a aucune importance pour ce qui est de ce tracé géométrique, mais en pratique, l’angle des rayons pouvant sortir d’un sténopé étant limité, incliner la planchette n’est pas sans influence sur la luminosité de l’objet. L’inclinaison de la surface portant le sténopé n’induira pas de distorsion supplémentaire, mais simplement un assombrissement dissymétrique des bords de l’image par obstruction des rayons les plus inclinés.
Figure 3: Projection d’un cercle et d’un carré sur un plan parallèle à l’objet
Figure 4: Projection d’un cercle et d’un carré sur un plan incliné
1.2 Distorsion en trapèze lors de la photographie d’une façade d’édifice
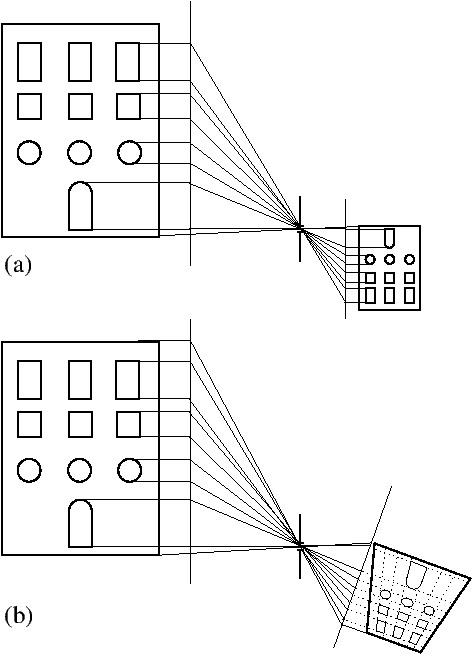
Le tracé de perspective de la camera obscura explique directement la distorsion en trapèze que l’on obtient en photographiant la façade d’un édifice avec une camera obscura penchée vers le haut ;nous montrerons dans la suite de l’article que ce tracé reste valable pour un appareil photo équipé d’un objectif, dans presque tous les cas d’usage pratique.
Figure 5: Camera obscura et distorsion en trapèze - (a) Avec décentrement vertical, plan de projection parallèle au plan de la façade - (b) En pointant un appareil dépourvu de mouvements vers le haut, le plan de projection devient incliné par rapport au plan de l’objet photographié
Pour éviter la distorsion en trapèze, que ne laissent jamais apparaître ni les artistes de la Renaissance, ni par la suite, aucun peintre ni aucun photographe d’architecture respectueux des règles anciennes (distorsion due à la projection, et qui n’est pas liée à la distorsion optique intrinsèque d’un objectif), il suffit d’utiliser le décentrement vertical, ce qu’il est possible de faire facilement avec une chambre ou une optique à décentrement (figure 5a), ou encore par correction via un post-traitement numérique, ce qui n’est pas toujours si facile.
Pour plus d’information sur l’usage des décentrements, nous renvoyons le lecteur à cet article [2] publié sur www.galerie-photo.com.
2 Puis vint la lentille mince convergente
2.1 Tracé de rayons dans une lentille mince convergente diaphragmée
On passe à la lentille mince convergente diaphragmée en son centre, diaphragme fermé.
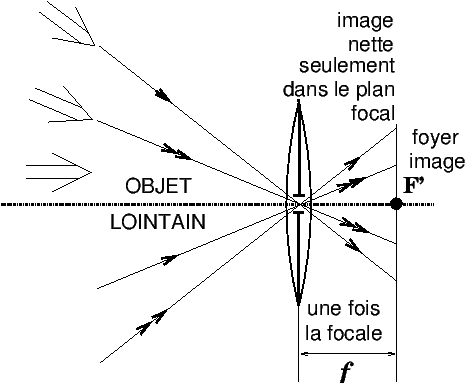
Figure 6: Lentille mince convergente diaphragmée en son centre, diaphragme très fermé
Selon l’un des principes de base de l’optique géométrique [3] -[4], tout rayon passant par le centre de la lentille mince n’est pas dévié. On s’aperçoit sur la figure 6 que le tracé de rayons à gauche comme à droite de la lentille est exactement celui du sténopé, avec la contrainte supplémentaire de devoir détecter l’image en projection sur une surface plane, appelé plan focal si on veut voir se former l’image nette d’un objet lointain. La distance focale est l’une des caractéristiques de base de la lentille mince, le plan focal est un plan perpendiculaire à l’axe optique, situé à une fois la distance focale derrière la lentille mince.
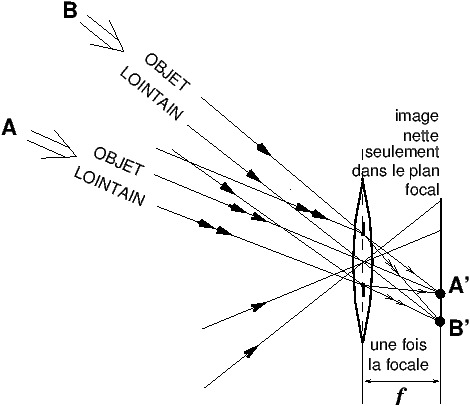
2.2 Lentille mince convergente, diaphragme ouvert, objet lointain
Puis on passe à la lentille mince convergente diaphragmée en son centre, mais cette fois on ouvre le diaphragme, l’objet est toujours lointain. Le nouveau tracé de projection (figure 7) ne change absolument pas vis à vis du cas précédent (figure 6), on doit juste respecter les conditions de conjugaison objet-image pour avoir une image nette des objets lointains : le détecteur doit être plan et placé au plan focal. On peut donc se contenter de ne tracer que les rayons passant par le centre de la lentille (appelés rayons moyens), comme c’est le cas lorsque la lentille est très diaphragmée. Bien entendu, l’ouverture du diaphragme joue un rôle primordial dans la luminosité des images, les questions de profondeur de champ, et les aberrations résiduelles, qui en général sont de moins en moins gênantes au fur et à mesure qu’on diaphragme (sauf la distorsion, intrinsèque à l’objectif, [5]). Mais le fait que le diaphragme soit ouvert, dans ce tracé de rayons purement géométrique, ne joue aucun rôle dans la détermination de la position et de la grandeur des images.
Figure 7: Lentille mince convergente diaphragmée en son centre, diaphragme ouvert, objet lointain
Pour un objet lointain, avec diaphragme ouvert, on complète le tracé des rayons moyens par le tracé des rayons s’appuyant sur le bord du diaphragme. Si la lentille est suffisamment diaphragmée pour que ses aberrations géométriques soient faibles, tous les rayons issus d’un même faisceau parallèle incliné se recoupent en un même point du plan focal image. Mais là encore, la projection ne change pas par rapport au cas précédent, on pourrait se contenter de tracer le rayon moyen passant par le centre du diaphragme supposé placé au centre de la lentille.
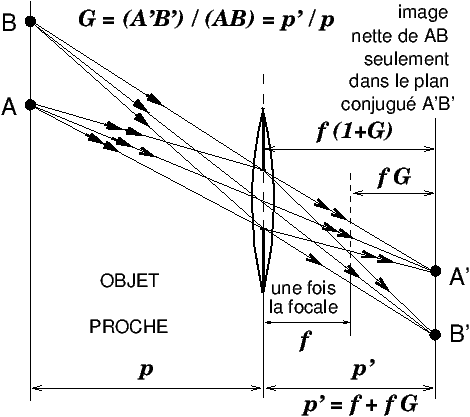
2.3 Lentille mince convergente, diaphragme ouvert, objet proche
Puis on passe à la lentille mince convergente
diaphragmée en son centre, diaphragme ouvert, mais objet à distance proche. Le
tracé de rayons se modifie en tenant compte de ce que l’image nette se forme
cette fois en arrière du plan focal, à une distance égale à f G
derrière le foyer, soit une distance totale f (1+G) derrière le
plan de la lentille.
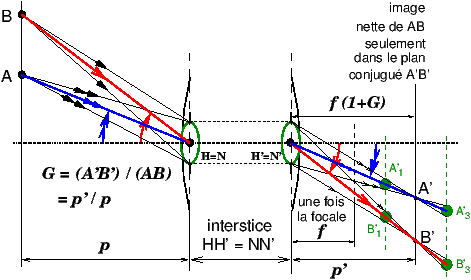
G désigne le grandissement : G=(A′B′)/(AB) = (p′/p),
rapport entre la dimension de l’image et la dimension de l’objet, qui est égal
au rapport des distances p′ et p séparant l’image et l’objet du
plan de la lentille mince. Pour un objet à l’infini, on a G=0 et l’image
se forme au plan focal.
Le lecteur qui souhaite connaître plus de détails sur l’origine de cette formule et sur les formules de conjugaison se reportera aux références [3] et [4].
Mais là encore, si on néglige les aberrations géométriques de la lentille, le tracé de projection est exactement le même que pour un sténopé où la projection s’effectuerait cette fois à la distance f (1+G). On notera en particulier que ces valeurs de grandissement sont exactement les mêmes pour la lentille mince (figure 8) que pour le sténopé (figure 1).
Figure 8: Lentille mince convergente diaphragmée en son centre, diaphragme ouvert, objet à distance proche
3 Enfin M. Carl
Friedrich Gauß formalisa
la théorie des systèmes optiques centrés
3.1 Système centré épais, tracé symbolique
Ensuite on passe au système centré épais, dont le formalisme a été élaboré par le célèbre mathématicien Carl Friedrich Gauß au XIXesiècle [6]. On appelle système optique centré l’assemblage de dioptres ayant une symétrie de révolution autour d’un axe commun. C’est à dire en pratique un assemblage de lentilles épaisses et de miroirs présentant une symétrie de révolution autour d’un axe commun. La lentille mince est l’exemple le plus simple d’un système optique centré, la lentille épaisse est formée de deux dioptres dont les sommets sont distants d’une certaine épaisseur qu’on ne peut plus négliger.
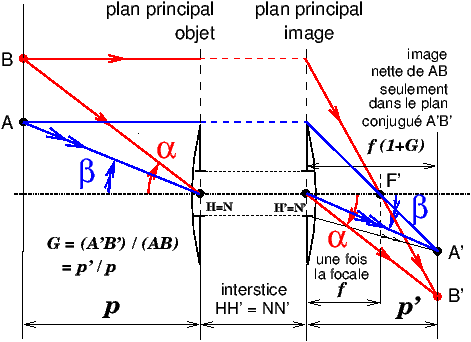
Pour déterminer la position et la grandeur des images, dans un système optique centré, pour des rayons peu inclinés et des petits objets placés près de l’axe optique, un tracé géométrique symbolique suffit, dans lequel on ignore la présence du diaphragme et des montures des lentilles. En plus de la distance focale, il suffit de uniquement de connaître l’écart entre les plans principaux H et H’ du système. Par définition de la distance focale f on a f=FH=H′F′ (pour plus de détails, voir les références [3] et [4]).
Ce tracé purement géométrique est valable pour un système centré quelconque, même totalement dissymétrique. Ce tracé symbolique peut se contenter des seuls rayons moyens, c’est à dire uniquement ceux passant par (ou qui pourraient passer par) les points nodaux N=H et N’=H’ (égalité valable si l’entrée et la sortie des rayons sont dans l’air, cas photographique le plus courant) ou les foyers F et F’ sur l’axe optique.
Figure 9: Système centré épais, on ne tient pas compte du diaphragme et des montures, tracé géométrique symbolique général pour la position et la grandeur des images nettes ; dans l’approximation de Gauss, il suffit de connaître la focale et la position des plans principaux
Pour mener à bien le tracé, on peut prolonger les plans principaux autant que l’on veut de part et d’autre de l’axe optique, et tracer des rayons aussi inclinés que l’on veut, ce qui n’est pas le moindre des paradoxes vu le domaine de validité de l’approximation de Gauss !
Bien entendu ce tracé géométrique, le tracé de rayons dans l’approximation de Gauss, n’a qu’une utilité très limitée pour l’ingénieur qui conçoit les objectifs, mais il reste néanmoins d’un grand intérêt pour le photographe, puisqu’il permet de déterminer la position et la grandeur des images, donc le cadrage possible et la mise au point nécessaire.
Lorsqu’on se place au voisinage de l’objet, au départ des rayons, ou à leur arrivée sur l’image, le tracé de rayons de l’approximation de Gauss représente assez bien la réalité ; mais ce qui se passe effectivement dans l’objectif, juste à l’entrée, à l’intérieur des verres, puis juste à la sortie, n’est pas représenté du tout par cette approximation. On peut donc se faire l’idée suivante ; les ingénieurs concevant des optiques photographiques passent leur vie à ce que leurs objectifs, en particulier les grand-angulaire à faible distorsion, fonctionnent au voisinage de l’arrivée des rayons sur l’image, exactement comme dans le tracé de rayons de l’approximation de Gauss, dont le tracé aurait été extrapolé avec des angles très inclinés. Il suffit donc, en principe, de connaître la focale et la position des plans principaux de l’objectif pour connaître où se forment les images, ce qui permet de régler la mise au point de l’appareil et de déterminer quelle sera la grandeur des images, donc comment s’effectuera le cadrage de la scène.
L’un des points-clés du tracé selon l’approximation de Gauss est que pour un système centré fonctionnant dans l’air, les points nodaux N et N′ sont confondus avec les points principaux H et H′. D’après la propriété fondamentale des points nodaux, l’angle entre le rayon moyen et l’axe optique est conservé (arcs fléchés rouges et bleus sur la figure 9). Donc les deux parties du tracé, à gauche de N et à droite de N′, sont exactement identiques à celui de la lentille mince, et la projection est donc la même que pour un sténopé.
Fondamentalement, le fait d’utiliser un système optique épais ne change donc rien en termes de projections et de perspectives à ce qui se passe avec un sténopé, du moins si on se restreint à la correspondance entre objets plans et images nettes se formant dans un plan [7].
3.2 Système quasi-symétrique avec les pupilles dans les plans principaux.
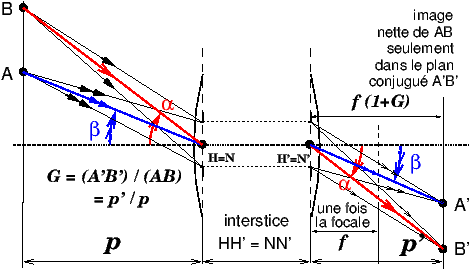
Dans ce cas particulier, on peut tenir compte très facilement de l’ouverture finie des faisceaux. Mis à part l’écart HH′ entre les plans principaux (appelé interstice), absolument rien ne change par rapport au cas de la lentille mince, car on peut montrer que dans un système symétrique, les deux images du diaphragme en entrée et en sortie, appelées pupilles sont de même diamètre [8]. Il en sera de même dans tout système dont les deux pupilles sont de même diamètre (on dit que dans ce cas le grandissement pupillaire est égal à 1).
La figure 10 est donc absolument identique à celle de la lentille mince (figure 8) diaphragmée en son centre, figure qu’on aurait découpée avec des ciseaux selon le plan de la lentille, puis qu’on aurait écartée en deux parties en coulissant le long de l’axe optique, distantes de NN′.
Figure 10: Système centré épais, de type quasi-symétrique avec pupilles aux plans principaux
4 Oui, mais on ne photographie pas que des objets plats !
Le lecteur qui aura eu la bonne volonté de nous suivre dans ce cheminement tout autant historique que géométrique doit probablement contenir son impatience avec difficulté, car depuis que les plans conjugués ont été évoqués ici, il a forcément en tête cette objection imparable :
« Tout ceci n’est que théorie amusante mais un peu inutile. Certes, j’ai le plus grand respect pour M. Gauß, ainsi que pour ces bénédictins de la haute époque de la photogravure analogique qui passaient leurs journées à peaufiner leurs prises de vues de documents plats avec leur banc de reproduction. Mais moi, je ne prends en photo que des scènes ou des personnages réels, qui sont tout sauf plats !! Et je connais parfaitement tout ce qui concerne les questions de profondeur de champ !
La suite de l’article, espérons-le, va rassurer notre lecteur : ni M. Gauß ni les photograveurs n’ont jamais interdit de photographier des scènes tridimensionnelles pour les réduire en des images planes. Même plus : les excellents objectifs pour banc de reproduction, en principe prévus pour ne travailler qu’à une distance donnée, avec une grandissement fixé, délivrent aussi d’excellentes images d’objets à l’infini et sont parfaitement capables de donner des très bonnes images d’objets volumiques, voire même volumineux.
Mais pour cela, comme on ne peut tout de même pas échapper à la conjugaison entre deux plans [9] si on veut la netteté absolue, il faudra bien se résoudre à ce que, lors de la prise de vue d’objets en volume, ou de plans étagés en profondeur, une partie de l’image soit plus ou moins défocalisée.
4.1 Système quasi-symétrique, pupilles aux plans principaux et images défocalisées
Passons donc maintenant au problème des images défocalisées dans un système quasi-symétrique.
Figure 11: Système centré épais, de type quasi-symétrique avec pupilles aux plans principaux et images défocalisées
La figure 11 montre que les images défocalisées s’obtiennent par projection conique de la pupille de sortie, le centre de projection étant le point-image net (A′ ou B′ sur la figure 11). Chaque faisceau issu d’un point-image net (A′ et B′ sur la figure 11) se projette sur un plan qui ne correspond pas à l’image nette sous forme d’une tache qui a la même forme que le diaphragme. Pour simplifier, on le supposera circulaire. La tache défocalisée, pseudo-image d’un point source, est donc un petit disque (représenté en vert foncé sur la figure 11). Le diamètre de ce disque augmente en proportion directe de l’écart au meilleur plan de mise au point.
Le centre de ce cercle de défocalisation est situé exactement où on attendrait que se forme une tache-image dans un sténopé, sur un plan de projection placé perpendiculairement à l’axe optique, à une distance arbitraire de part et d’autre du plan d’image nette.
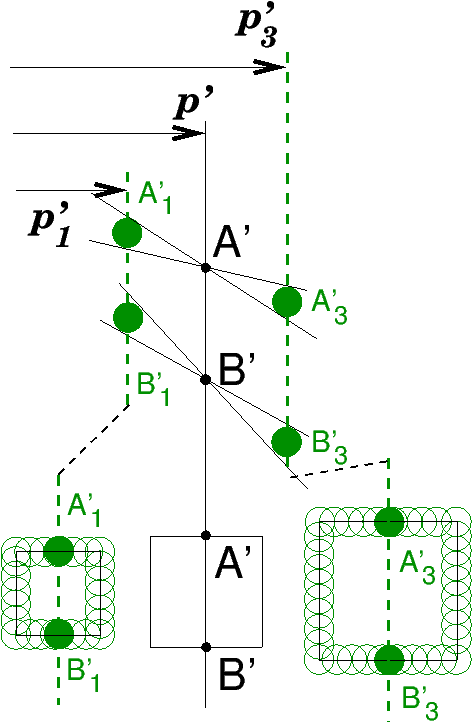
La figure suivante 12 montre l’aspect de l’image d’un carré lorsqu’il y a défocalisation [11].
Figure 12: Images défocalisées d’un carré dans un système optique quasi-symétrique
Cette propriété très remarquable de l’image optique défocalisée, qui est affectée d’un facteur de grandissement qui se déduit exactement du tracé de la camera obscura, n’existe que lorsque les pupilles sont placées dans les plans principaux. En effet, l’image défocalisée d’un point de l’objet est obtenue comme la projection conique de la pupille de sortie, le centre de projection étant le point-image net. La position du centre de ce petit cercle de flou est celle qu’on attendrait d’une projection derrière un sténopé, mais uniquement parce que le point H’=N’ est situé au niveau de la pupille de sortie. En effet, au rayon moyen AN en entrée correspond en sortie le rayon moyen N′A′ avec la même inclinaison, parce que N et N′ sont les points nodaux du système. De plus, lorsque la pupille de sortie est placée au plan principal H′=N′, les taches de défocalisation A′1 et A′3ont leurs centres parfaitement alignés avec le rayon moyen N′A′ (figures 11 et 12). Cette propriété qui rend la projection des images défocalisées exactement analogue à celle de la camera obscura est liée à la position particulière des pupilles dans les plans principaux, situation de l’objectif symétrique, ou dont le grandissement pupillaire est égal à l’unité.
4.2 Système dissymétrique dont les pupilles ne sont plus placées aux plans principaux
Lorsque cette condition de symétrie de l’objectif n’est plus réalisée, ce qui est le cas dans les optiques dissymétriques comme les téléobjectifs, rétrofocus ou autres optiques spéciales comme les objectifs télécentriques, les images défocalisées sont affectées d’un grandissement plus complexe à calculer [12].
De plus, même dans une projection entre plans parallèles, une étrange distorsion va apparaître dans les images défocalisées d’une optique où les pupilles ne sont pas placées dans les plans principaux, lorsqu’on incline l’objectif en conservant les plans objet et image bien parallèle.
Avec une caméra à sténopé, une lentille mince ou un système optique dans lequel les pupilles sont placées dans les plans principaux, pencher l’objectif entre plans objet et image parallèles n’induit aucune distorsion en trapèze, contrairement à ce qui se passe avec un appareil qui ne peut pas décentrer lorsqu’on le pointe vers le haut ou vers le bas en cadrant, par exemple, une façade verticale. Cette règle bien connue des photographes à la chambre depuis l’invention de la photographie, tombe en défaut si on travaille avec un rétrofocus ou un téléobjectif. Pour avoir une idée de ce phénomène, nous renvoyons le lecteur à cet article sur galerie-photo [13].
5 De quoi dépend le rendu de perspective ?
5.1 Distorsion des sphères en bord de champ d’un grand-angulaire
L’un des grands avantages de la photo au sténopé est que, moyennant d’accepter la perte de cette netteté qui caractérise les belles images optiques qui se forment derrière nos chers objectifs, et moyennant d’accepter une très faible luminosité d’image, on dispose à peu de frais de l’équivalent d’un grand-angulaire dépourvu de distorsion.
Mais attention : si le sténopé est effectivement exempt de cette distorsion optique intrinsèque contre laquelle les ingénieurs se battent lorsqu’ils calculent leurs objectifs [10], il reste tout de même un effet particulier de distorsion des sphères qui apparaît sur le bord des images prises au sténopé ou avec un objectif grand-angulaire même si le plan sur lequel sont posées les sphères est parfaitement parallèle au film (voir figure 13). Là encore, cet effet est inévitable et devient très visible avec les ultra-grands angles de champ à partir de 90° et au-delà. Cette déformation est gênante, par exemple, si on photographie un groupe de personnes au grand angulaire, les visages de ceux qui sont en bord de champ seront affectés d’un étirement peu esthétique.
Figure 13: Même si le plan objet est bien parallèle au plan image, l’image projetée d’une sphère posée sur le plan objet est une ellipse d’autant plus allongée qu’on s’éloigne de l’axe optique. La raison en est que la ligne délimitant la partie visible de la sphère est un cercle de plus en plus incliné par rapport au plan d’appui de la sphère, d’où la déformation en ellipse de ce contour en projection dans l’image.
5.2 Perspective conique, le rendu de perspective ne dépend que du point de vue
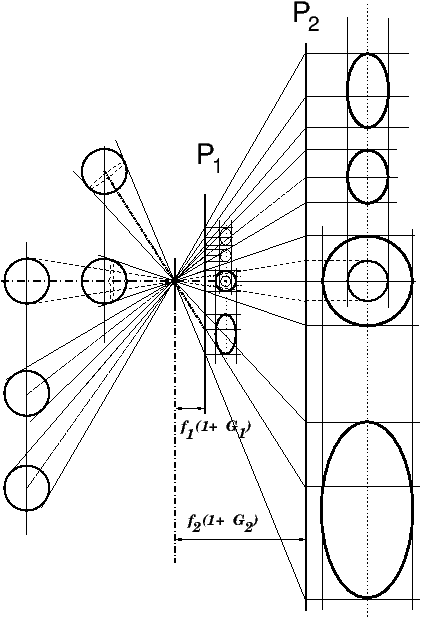
Nous nous placerons ici pour simplifier dans le cas d’une optique où les pupilles sont placées dans les plans principaux. Sous cette hypothèse, à la fois les images nettes et les images défocalisées peuvent être construites par le tracé symbolique de l’appareil à sténopé où la détection s’effectue dans un plan. On s’arrange pour que les pupilles d’entrée des objectifs soient placées au même endroit par rapport à la scène, dans ces conditions le tracé de projection dans l’espace image est identique à celui du sténopé, l’espace image étant simplement décalé vers l’arrière de la distance HH’. Les différentes focales des objectifs utilisés vont simplement correspondre, dans le tracé, à différentes distances entre la pupille de sortie (placée en H’= N’) et le plan de projection où va se former l’image, ce plan n’ayant aucune obligation d’être perpendiculaire à l’axe optique (figure 14).
Figure 14: Le rendu de perspective ne dépend que du point de vue ; les images projetées par différents objectifs de différentes focales, dont la pupille d’entrée est placée au même endroit, se déduisent l’une de l’autre par une homothétie dans le rapport des distances de projection (le rapport des focales si les objets sont placés loin, sinon c’est le rapport distances de mise au point f (1+G)), le rendu des objets volumiques, leurs alignements, est exactement le même. La projection des sphères dans le plan P2 se déduit de celle dans le plan P1 par une simple homothétie de rapport (f2 (1+G2)/f1 (1+G1)).
Conclusion
-
Pour tout ce qui concerne le tracé géométrique donnant la grandeur des images et la projection de l’ensemble de l’espace objet à travers une optique photographique, on peut se contenter du modèle du sténopé dans la plupart des cas.
-
Avec toutes les optiques quasi-symétriques, celles dont les pupilles sont placées dans les plans principaux, le placement des objets en projection et leur dimension dans l’image – que l’image soit nette ou défocalisée – peuvent être simulés par le tracé de rayons de perspective conique connu depuis la Renaissance.
-
Seul le cas des images défocalisées avec une optique dissymétrique –dans laquelle les pupilles ne sont pas placées dans les plans principaux– ne peut pas être simulé simplement avec la construction classique de la camera obscura.
Tous les éléments sont donc maintenant en place pour aborder la question du rôle de la pupille d’entrée dans le raccordement panoramiques d’images, ce qui fera l’objet d’un autre article.
Notes et Références
|
Parmi les plus
célèbres tableaux en anamorphose, il y a le fameux tableau de Holbein le
jeune, Les ambassadeurs (1533). |
|
|
« Décentrements,
bascules et règle de Scheimpflug en petits et moyens formats », E.
Bigler, |
|
|
« Un objectif
photographique n’est pas une lentille mince ! »Première partie,
introduction aux systèmes optiques centrés épais, par Emmanuel Bigler et
Yves Colombe |
|
|
Moussa/Ponsonnet, « Optique géométrique » Cours de physique, tome 1. Optique , Casteilla (2000) ISBN : 2713512239 |
|
|
Lorsqu’on diaphragme
une lentille, ou de façon plus générale un système centré, la qualité
d’image s’améliore ; l’aberration de sphéricité, la coma et
l’astigmatisme se réduisent. En revanche, la distorsion n’est pas
influencée par la fermeture du diaphragme. Dans une optique de haute
performance, la position du diaphragme est choisie avec le plus grand
soin ; une fois placé, la distorsion résiduelle ne disparaît pas en
diaphragmant. Pour une introduction à la distorsion, on peut regarder
cette page wikipédia : |
|
|
Carl Friedrich Gauß
(1777-1855) |
|
|
On peut étendre la
correspondance entre plans conjugués au cas de plans inclinés, selon la
règle de Scheimpflug. Voir ces articles surwww.galerie-photo.com. |
|
|
« Lumière, diaphragme
et pupilles, optiques épaisses -II », E. Bigler, |
|
|
La plupart des objectifs sont affectés de courbure de champ. Ce qui veut dire que l’image la meilleure, la plus nette, issue d’un plan-objet ne se forme pas sur un plan-image, mais sur une sphère. Pour simplifier, on ne tiendra pas compte ici de ce phénomène, qui joue cependant un rôle important dans les optiques ultra grand-angulaire. |
|
|
On peut montrer
qu’une combinaison optique parfaitement symétrique, avec l’iris placé au
centre de symétrie, donnera au rapport 1:1, c’est à dire dans la seule
configuration objet-image parfaitement symétrique, une image totalement
dépourvue de distorsion, de coma et de chromatisme transversal. Ce
principe de symétrie fut connu dès le XIXe siècle, et il est très
remarquable que des objectifs parfaitement symétriques comme les
apochromatiques de banc de reproduction (par exemple l’Apo Ronar et les
dialytes symétriques de formule 4/4) donnent également de très bonnes
images à l’infini et non pas seulement au rapport 1:1. La plupart des
optiques de chambre développées depuis près de 120 ans sont des formules
symétriques ou quasi-symétriques, même celles optimisées pour les
grandes distances de prise de vue. L’exception à ce principe de symétrie
étant les rétrofocus et les télé-objectifs, optiques dans lesquelles il
est bien plus difficile d’éliminer la distorsion et le chromatisme
transversal, auquel les capteurs silicium à matrice colorée de type
Bayer sont très sensibles. |
|
|
Le tracé d’images défocalisées de la figure 12 n’est valable que pour une forte défocalisation. Dans la pratique, aux faibles défocalisations, le modèle géométrique basé sur la projection de la pupille de sortie (figures 11 et12) ne représente pas correctement la réalité, parce que les taches de défocalisation géométriques sont masquées par les taches d’aberrations résiduelles. |
|
|
Par exemple, derrière un objectif télécentrique, les images défocalisées gardent pratiquement la même dimension que l’image nette, cette propriété très importante des objectifs télécentriques est mise à profit dans les machines optiques à mesurer sans contact comme les projecteurs de profil utilisés dans tous les ateliers de mécanique. |
|
|
« Décentrements,
bascules et règle de Scheimpflug en petits et moyens formats », E.
Bigler, |
Télécharger cet
article
au format pdf
dernière modification de cet article : 2013
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||