

l'auteur
|
Emmanuel Bigler
est professeur (aujourd'hui retraité) d'optique et des
|
Télécharger l'article
au format pdf
Au secours !
Mes verticales
penchent !
Par Emmanuel Bigler
mél
Table des matières
I Introduction
II Un peu d’histoire
II 1 La perspective au
Moyen-Âge
II 2 La perspective
depuis la Renaissance
III Comment se projette l’image
dans un objectif photographique ?
III 1 Cas des
objectifs quasi-symétriques
III 2 Cas des
objectifs dissymétriques
IV Conditions géométriques pour
la projection des verticales
IV 1 Projection
d’une ligne
verticale ou
d’un plan
vertical
IV 2 Projection
d’une façade,
« distorsion en
trapèze »
IV 3 Projection
d’une boîte
parallélépipédique,
vue en plongée
V Verticales et nutation lors
de l’application de bascules
croisées
VI Annexe 1 : les
grand-angulaires rétrofocus ne
fonctionnent pas
comme un
sténopé !
VII Annexe 2 : définition de
l’angle de nutation au sens de
la
mécanique du solide
Résumé
Dans cet article, nous réexaminons la question du rendu des verticales dans les photos d’architecture ou dans les photos d’objets en studio. Après un bref historique, on rappelle les conditions nécessaires pour obtenir de belles verticales bien verticales et bien parallèles dans l’image photographique prise avec une chambre ou un appareil pourvu de mouvements (bascules et décentrements). La question de la nutation parasite qui apparaît à cause de la combinaison de bascules croisées lors de la prise de vue avec certaines chambres est évoquée.
I Introduction
Il n’y a pas si longtemps
encore, à la fin du siècle dernier, certaines
catégories de photos de qualité professionnelle
ne devaient être prises qu’avec une chambre
grand format.
Il y avait à cela plusieurs raisons :
-
Les techniques de photogravure analogique exigeaient comme document de départ un négatif ou une diapositive d’excellente qualité ; plus la qualité souhaitée à l’impression était élevée, plus grand devait être le format de film à la prise de vue. Par exemple, en France, les catalogues de montres et de bijoux étaient presque toujours pris à la chambre de format 20x25 cm ;
-
Les images devaient être conformes à certaines règles strictes sur le plan géométrique. Par exemple les verticales des édifices en photo d’architecture devaient être rendues dans l’image sous forme de verticales et surtout pas sous forme de lignes convergentes « qui penchent » ; il en était de même pour toute prise de vue présentant des lignes verticales, par exemple dans les photos d’intérieurs ou de mobilier ;
-
Dans les travaux en couleur à partir de diapositives, le photographe professionnel livrait en vue de la photogravure une diapositive à son client, la prise de vue devait être parfaite sur le plan de la netteté, de la justesse de l’exposition, de la colorimétrie, du cadrage et du rendu de perspective. Le photographe devait donc anticiper sur tous ces points en préparant sa prise de vue, car une fois l’obturateur déclenché, tout devait être parfait dans l’image et peu de retouches étaient possibles après le développement (à part un recadrage simple et certaines retouches colorimétriques en vue de l’impression par les techniques analogiques d’autrefois).
Toutes ces raisons faisaient de la chambre grand format l’outil professionnel par excellence, au point qu’en allemand la chambre grand format est souvent appelée « Fachkamera », l’appareil photo professionnel.
Avec l’abandon du film et de la chambre lors du passage à la prise de vue sur capteur silicium par la plupart des amateurs et des professionnels, au début de ce millénaire, les possibilités de post-traitement numérique ont rendu en apparence désuète cette manière de travailler, où tout devait être parfait au moment du déclenchement. En particulier le cadrage, la conformité à certaines règles géométriques dont « le respect des verticales bien verticales », ne sont plus nécessairement prises en compte à la prise de vue aujourd’hui, car parfois un post-traitement peut remettre les choses en place.
Il y a une dizaine d’années, lors de l’une des premières « Journées du patrimoine », avec ouverture au public d’édifices privés ou publics non accessibles en temps normal, les responsables du patrimoine à Besançon (FR-25) avaient édité une belle petite plaquette en couleurs, richement illustrée, pour attirer le public vers les beaux édifices anciens dont la vieille ville comtoise est fort riche. Quelle déception ! Sur une trentaine d’imagettes, aucune ne respectait les règles classiques de la projection des verticales.
Le silicium de la prise de vue n’était évidemment pas en cause, il fallait chercher les raisons de ces images très étranges dans le fait que les appareils utilisés étaient certainement dépourvus de toute possibilité de décentrement, et très souvent équipés d’objectifs grand-angulaires. Dans ces conditions, lorsque l’axe optique est penché vers le haut, et corrélativement le détecteur penché vers l’arrière (sauf cas très particulier des optiques de petit et moyen format à bascule et décentrement), les verticales convergent et penchent, un résultat très désagréable visuellement (bien que parfaitement normal sur le plan purement géométrique) ; des « murs qui penchent » qu’on retrouve, hélas, sur beaucoup d’illustrations des pages de Wikipédia et de certaines pages web, pourtant consacrées à la sauvegarde du patrimoine (voir par exemple ces illustrations [1], [2], [3]).
Certes, sur Wikipédia, les illustrations sont fournies par des bénévoles, et nous en sommes très heureux, mais il n’est pas inutile qu’un photographe, même bénévole (donc non soumis aux mêmes obligations de résultats qu’un professionnel), ait connaissance de ce qui était la norme de la prise de vue de qualité depuis que la photographie fut « révélée » au monde en 1839.
II Un peu d’histoire
II 1 La perspective au Moyen-Âge
Sans quitter notre vieille
Europe, regardons comment les édifices étaient
représentés au Moyen-Âge dans les dessins et les
peintures.
Par exemple dans les fresques de Saint Savin
(FR-86) [4]
on peut voir une tour médiévale de section
carrée, les verticales sont bien verticales mais
les côtés de l’espèce de terrasse surmontant la
tour sont parallèles, comme dans une
perspective
cavalière en dessin industriel, à
l’époque pas si lointaine où on traçait tout à
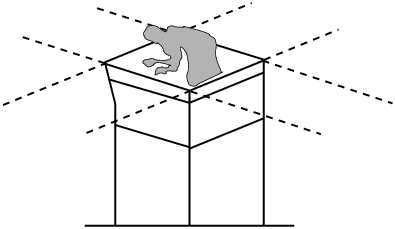
la main sur une planche à dessin (figure 1).
|
|
Figure 1: Lignes schématiques, d’après l’une des fresques de Saint-Savin, cette tour médiévale est représentée un peu comme dans une perspective cavalière.
Il n’y a donc aucun point de fuite dans cette image, ni pour les lignes verticales, rendues verticales et parallèles, ni dans les lignes horizontales parallèles du sujet, rendues également parallèles. Mais déjà au Moyen-Âge, les verticales sont dessinées bien verticales !
II 2 La perspective depuis la Renaissance
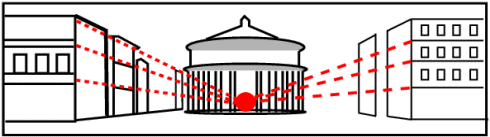
À la Renaissance, on élabore les lois de la perspective en projection conique, ou perspective en tableau [5] dans laquelle les verticales des édifices sont toujours représentées strictement verticales ; en revanche les lignes horizontales parallèles sur les parties des édifices vues de côté, convergent vers un point de fuite. L’exemple emblématique de cette représentation en perspective « moderne » est la Cité idéale d’Urbino (≃1480 - 1490, œuvre initialement attribuée à Piero de la Francesca [6]), figure 2.
|
|
Figure 2: Lignes schématiques, d’après le tableau de la « Cité idéale d’Urbino », les édifices sont représentés selon la perspective conique « moderne », les verticales sont verticales, les horizontales pour les plans qui ne sont pas vus de face, convergent vers un point de fuite.
Cette manière classique de
représenter l’architecture n’a plus jamais
changé par la suite.
Imaginerait-on des « Noces de Cana » de
Véronèse [7]
dans lesquelles les colonnades pencheraient,
menaçant d’écraser la foule dans une chute
effroyable ? Cela dit, les artistes du XVe
siècle n’avaient pas peur des contre-plongées
audacieuses ! [8]
Mais quant il s’agit de bâtiments, même dans la vue du chevet de l’église d’Auvers sur Oise [9], Van Gogh nous donne des verticales (presque) verticales !
Cependant, les lois mathématiques de la perspective conique n’interdisent absolument pas de représenter des verticales qui convergent vers un point de fuite ! C’est à dire exactement ce qu’on obtient en pointant l’axe optique de son appareil photo vers le haut, le film ou le détecteur étant perpendiculaire à l’axe optique.
Représenter les verticales des édifices comme verticales est une règle esthétique classique, une règle conventionnelle à laquelle tous les dessinateurs et les peintres se sont conformés depuis la fin du XVe siècle.
Lors de l’invention de la photographie au XIXe siècle, il était d’autant plus clair pour les premiers photographes qu’il fallait se conformer à cet usage, que l’appareil photographique n’est que le perfectionnement de la chambre à sténopé ou camera obscura, la chambre noire [10], utilisée, justement, pour aider au tracé des perspectives coniques depuis la Renaissance. Mais rien n’interdit de pointer sa chambre à sténopé vers le haut, on verra alors les verticales converger, bien entendu !
On peut tout de même ajouter une raison physiologique à cette règle demi-millénaire de représentation des verticales des édifices sous forme de ... verticales et non pas sous forme d’un faisceau de lignes convergentes.
La vision humaine ne se résume pas à la simple projection d’une image sur la surface sphérique de la rétine. Ces images « optiques » sont ensuite interprétées par notre admirable réseau de neurones, ne serait-ce que le redressement haut-bas, qui nous fait voir le haut en haut et le bas en bas, alors que l’image rétinienne est tournée de 180° à cause de ces fichues lois de l’optique !
On ne s’étonnera donc pas qu’une telle machinerie complexe, (totalement analogique, soit dit en passant !), celle du post-traitement neuronal des images nous fasse voir les verticales sous forme de lignes parallèles, et non pas convergentes ! Notre système de vision humaine combine de façon extraordinaire les capacités d’une très longue focale photographique, un angle de champ très réduit de l’ordre de 5° (la zone de la rétine qui enregistre ces images à haute résolution s’appelle la fovea ; dans cette zone centrale, la qualité de l’image atteint la limite de diffraction par la pupille) avec les capacités d’un ultra-grand angulaire (presque 180° d’angle pour la vision périphérique, mais avec une résolution très réduite).
Lorsque nous regardons la façade de l’église Saint Pierre de Besançon [1], ou lorsque nous sommes à Montbéliard pour le marché de Noël, sur la place du temple [11], jamais nous ne voyons les verticales des édifices « se pencher ». Notre vision enregistre une succession d’images à haute résolution avec un angle de champ réduit de 5°, et pour voir les verticales pencher, il faudrait vraiment se mettre « au pied du mur » et incliner la tête vers le haut au point de se faire mal aux vertèbres cervicales.
En d’autres termes, les images photographiques prises avec un objectif grand-angulaire sont (presque) toujours conformes au « lois mathématiques de la perspective », mais ce qu’elles représentent est, en général, inaccessible à la vision humaine qui procède par « raccordement de champs » ne dépassant pas 5° d’angle.
III Comment se projette l’image dans un objectif photographique ?
Malgré tout le respect que nous portons à la chambre à sténopé, ne serait-ce que par le rôle éminent qu’elle joue pour aider au tracé des dessins de perspective depuis la Renaissance, avouons que nous préférons, et de loin, la netteté d’image extraordinaire que peuvent nous donner les objectifs modernes, en particulier, pour les vues d’architecture, ce qu’il est possible d’obtenir avec les grand-angulaires de chambre conçus à la fin du XXesiècle : certains couvrent jusqu’à 120° d’angle, pratiquement sans distorsion !
La plupart des cours de photographie admettent sans démonstration que l’image projetée par une optique épaisse est, sur le plan géométrique et du rendu de perspective, exactement conforme à ce qu’on obtiendrait avec une chambre à sténopé. C’est à dire que le rendu de perspective est celui obtenu en lançant des rayons lumineux rectilignes issus de l’objet, passant tous en un point unique, celui du sténopé qui joue le rôle du centre de projection de la perspective conique ; le détecteur enregistre ce qui est géométriquement l’intersection des rayons avec un plan de projection qui peut, idéalement, être incliné à volonté (figure 3).
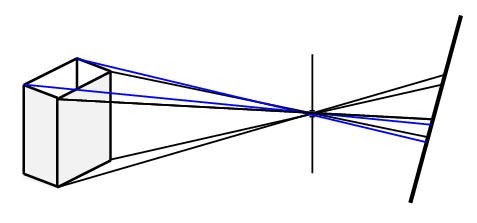 |
Figure 3: La plupart des cours de photographie considèrent, sans démonstration, que le rendu de perspective, pour les images qui se forment derrière un objectif, est exactement conforme au modèle du tracé de rayons de la chambre à sténopé.
Mais si on y regarde d’un peu plus près, des difficultés surgissent.
La première difficulté est que les objectifs modernes donnant les belles images bien nettes que nous aimons tant, sont des assemblages complexes de lentilles, il ne s’agit pas d’un simple trou de sténopé ! Certes, il y a bien à l’intérieur de l’objectif un diaphragme qui rappelle évidemment le trou du sténopé ; mais dans cet objectif que j’ai sous les yeux, où se trouve le « trou de sténopé équivalent » qui conditionne le rendu de perspective ?
La deuxième difficulté est
qu’on ne prend que très rarement des objets
plats en photo !
Le rendu des volumes en projection est donc un
problème important, et il faut accepter des
compromis entre la profondeur de champ et le
choix des projections. Le tracé de rayons de la
perspective conique, qui est identique à la
projection dans une chambre à sténopé, ne nous
dit évidement rien de la netteté de l’image. Or
il se trouve que la projection par un système
optique complexe, des images défocalisées,
s’effectue différemment selon le genre
d’objectif, selon qu’il est quasi-symétrique ou
dissymétrique ; le modèle du sténopé étant
a priori
insuffisant dès qu’on cesse de reproduire des
documents plats !
Nous rappellerons ici sans
démonstration les règles de la projection dans
les objectifs photographiques. Pour ceux qui
aiment comprendre par eux-mêmes et qui sont
allergiques aux « arguments d’autorité », nous
renvoyons à deux articles [12],[13]
publiés sur
https://www.galerie-photo.com
traitant de ces questions en détail.
Pour essayer de résumer en peu de mots : ce qui diffère fondamentalement entre la camera obscura et une chambre équipée d’un objectif, c’est le fait qu’avec un objectif, un sujet tridimensionnel est projeté comme la superposition d’images défocalisées sur l’image nette, celle qui est optiquement conjuguée du plan où le détecteur est installé. Les images défocalisées se projettent comme dans une chambre à sténopé uniquement lorsque les pupilles de l’objectif sont proches des plans principaux, c’est à dire dans le cas des objectifs quasi-symétriques.
Lorsque les pupilles ne sont plus placées aux plans principaux, c’est à dire lorsque le grandissement pupillaire de l’objectif diffère notablement de l’unité, la position et la grandeur des images nettes sont (et c’est heureux !) toujours celles qu’on peut estimer par les formules de l’optique géométrique paraxiale [16], [17], mais dans une optique dissymétrique, les images défocalisées n’obéissent pas du tout aux règles ordinaires du tracé de rayons de la camera obscura.
III 1 Cas des objectifs quasi-symétriques
Cette classe d’objectifs comprend tous les objectifs de focale « normale » des petits et moyens formats, tous les objectifs de chambre « standard », les objectifs « grand-angle » des appareils non reflex et des chambres. En optiques de chambre, les seules formules non symétriques sont les télé-objectifs ; il n’y a pas eu, à notre connaissance, de développement de formule grand-angulaire rétrofocus [14] (donc dissymétrique) pour les chambres « à film » grand format. Mais pour tous les appareils reflex de petit et moyen format, les grand-angulaires appartiennent tous à la famille des rétrofocus dissymétriques.
De nouveaux objectifs grand-angulaires de haute performance de type rétrofocus ont été développés récemment pour les appareils moyen format à capteur silicium [15].
-
Pour les objectifs quasi-symétriques, c’est à dire ceux dont le grandissement pupillaire [12] est proche de 1, la projection de l’image, qu’elle soit nette ou défocalisée, s’effectue comme à travers un sténopé [13]. Les deux pupilles sont placées aux plans principaux [16], [17], qui sont également les points nodaux, le rendu de perspective est exactement le même qu’à travers un sténopé (donc sans lentille aucune) qui serait placé au niveau de la pupille d’entrée de l’objectif ;
-
Lorsque le grandissement pupillaire est proche de 1, la pupille de sortie est très proche du plan principal image de l’objectif, qui par définition du plan principal image [16], [17] est situé à une fois la distance focale en avant du foyer image. La distance entre cette pupille de sortie et l’image nette d’un objet lointain est donc très proche de la distance focale de l’objectif. Donc pour les objets lointains, la grandeur de l’image et le rendu de perspective sont identiques à ce qu’on obtiendrait avec un appareil à sténopé, la distance sténopé-film étant égale à la focale de l’objectif ;
-
Avec un objectif quasi-symétrique, on peut tourner l’objectif autour d’un axe quelconque perpendiculaire à l’axe optique sans changer le rendu de perspective dans l’image, comme si c’était un sténopé. Bien entendu, tourner l’objectif (sauf en tournant autour de l’axe optique, qui est l’axe de symétrie de révolution du système optique !) ne maintient pas la netteté de l’image, loin s’en faut ! Mais les images défocalisées sont toujours formées de façon analogue au cas du sténopé.
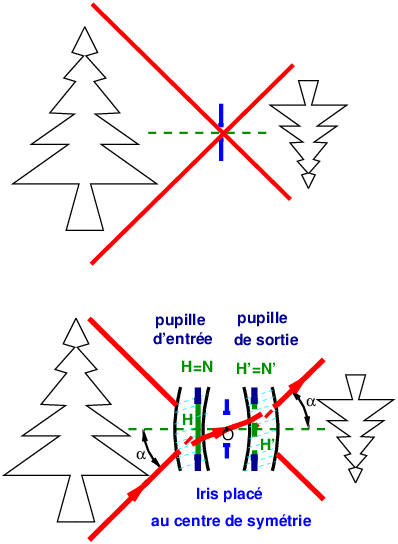 |
Figure 4: Dans une optique symétrique, avec l’iris placé au centre de symétrie, le rendu de perspective en projection est exactement le même que dans dans une chambre à sténopé.
III 2 Cas des objectifs dissymétriques
-
Pour tous les objectifs, quasi-symétriques ou dissymétriques, télé-objectifs ou grand-angulaires rétrofocus, c’est la position de la pupille d’entrée qui conditionne le rendu de perspective, c’est à dire ce qui est vu ou caché dans l’espace objet, et les alignements des objets ;
-
Dans la plupart des objectifs dissymétriques, le rendu de perspective reste assez proche de ce qu’on obtiendrait en se basant sur le modèle du sténopé. Néanmoins dans certaines circonstances très particulières (voir annexe 1, paragraphe VI), avec des optiques à grandissement pupillaire très différent de l’unité, la projection des images défocalisées diffère de ce qu’on aurait avec un sténopé, en particulier, une rotation de l’objectif peut induire une distorsion « non classique ».
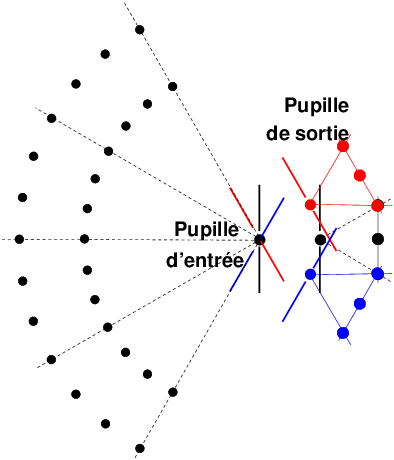 |
Figure 5: Dans le cas général, on peut toujours dire que le rendu des alignements dans l’espace objet et le rendu de perspective sont imposés par le placement de la pupille d’entrée de l’objectif, mais la projection des images défocalisées n’est pas la même qu’avec un sténopé ou une optique symétrique.
Mais fort heureusement, dans la plupart des cas, même si l’objectif est dissymétrique, le modèle du tracé de rayons dans un sténopé donne une bonne approximation de ce qu’on obtient avec un objectif.
Si l’objectif est parfaitement symétrique, avec un grandissement pupillaire égal à 1, le modèle du sténopé représente parfaitement la réalité, pour ce qui concerne le grandissement et le rendu de perspective. Plus le grandissement pupillaire de l’objectif s’écarte de l’unité, donc plus l’objectif est dissymétrique, moins le modèle de tracé de rayons du sténopé représente correctement la réalité, par exemple dans le cas d’un grand angulaire rétrofocus (voir l’annexe 1, paragraphe VI).
Mais dans la
plupart des cas, la
camera obscura
de la Renaissance saura être un guide fidèle
pour l’action !
Dans tout ce qui suit, nous nous appuierons donc uniquement sur le modèle du sténopé dans la représentation des projections, en particulier la recherche des verticales bien verticales ; ce qui permettra de réduire l’étude à quelques tracés de perspective très simples.
Le fait que le tracé de rayons du sténopé suffise presque toujours à expliquer le grandissement des images et le rendu de perspective, a deux conséquences très importantes (valables en toute rigueur uniquement dans la limite de pertinence du modèle, objectifs quasi-symétriques) :
-
En photographie, le rendu de perspective ne dépend pas de la focale de l’objectif, il ne dépend que de la distance entre la pupille d’entrée et le sujet ;
-
Une rotation de l’objectif, donc l’application de bascules à l’avant de l’appareil est sans effet sur le rendu de perspective, seul importe le placement du dépoli de chambre, ou le placement du plan du capteur, c’est à dire son inclinaison dans l’espace ; la netteté en revanche dépend beaucoup de l’application de bascules à l’avant ;
-
La maîtrise du rendu de perspective en projection dépend donc entièrement des bascules appliquées à l’arrière.
IV Conditions géométriques pour la projection des verticales
Après cette très longue présentation, nous voici enfin au cœur du sujet : comment faire pour que les verticales du sujet soient rendues sous la forme de verticales bien verticales et parallèles dans mon image ?
Comme expliqué précédemment, nous allons oublier l’objectif et le remplacer par un trou de sténopé, afin de ne pas nous encombrer, du moins au départ, des considérations sur la distance correcte entre les deux corps de chambre et l’inclinaison correcte du plan de l’objectif qui donnera une bonne netteté, selon la règle de Scheimpflug.
La règle de Scheimpflug pour les bascules est une condition nécessaire qui impose le placement et l’inclinaison de la planchette d’objectif pour que la netteté soit réalisée lorsque le plan objet et le plan image ne sont pas parallèles ; si le plan objet est parallèle au plan du film ou du détecteur, alors la planchette d’objectif doit être parallèle à ces deux plans, c’est le cas des appareils « ordinaires » dépourvus de mouvements.
Nous ne parlerons pas ici de cette règle de base de la prise de vue à la chambre, nous renvoyons aux cours classiques de photographie en grand format [18], [19], [20], [21], [22] ainsi qu’à trois articles sur [23], [24] , [25] publiés sur https://www.galerie-photo.com.
IV 1 Projection d’une ligne verticale ou d’un plan vertical
Partons d’un plan de référence horizontal, sur lequel nous allons dresser de fines tiges bien rectilignes et bien verticales que nous voulons photographier. Si le plan du film est vertical, même s’il est incliné droite-gauche, la projection des tiges sur le plan du film va nous donner des lignes droites verticales. Droites parce qu’il n’y a pas de distorsion avec un sténopé, et verticales pour les raisons géométriques suivantes (figure 6).
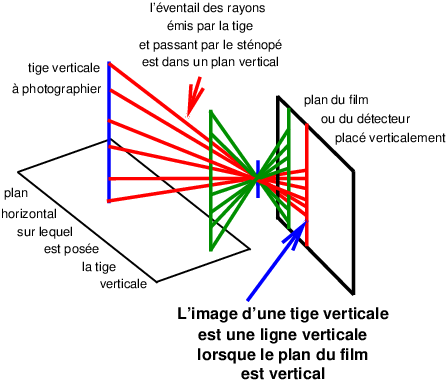 |
Figure 6: Pour que l’image d’une ligne verticale soit verticale, il suffit que le plan du film soit vertical.
Imaginons l’éventail des rayons lumineux issus d’une de ces tiges verticales, rayons qui passent par le trou du sténopé. Cet éventail diverge ensuite pour percer le plan du film. L’ensemble des rayons possibles est donc contenu dans un plan qui passe par la tige et le trou du sténopé. La tige étant verticale, ce plan est vertical. Le plan du film étant lui aussi vertical, l’image de la tige est donc l’intersection de ces deux plans verticaux, le plan contenant l’éventail des rayons lumineux, et le plan du film.
Cette intersection de deux plans verticaux est donc une ligne bien droite et bien verticale.
Il en est de même de toutes les tiges placées verticalement sur le plan de référence, leurs images nous donneront un bel ensemble de lignes droites verticales dans l’image, si le plan du film est bien vertical.
Restreignons le plan du film à la surface rectangulaire d’un plan-film, et supposons que deux côtés du film soient bien verticaux ; les autres côtés seront donc horizontaux. Dans ces conditions, si nous choisissons bien la distance entre le trou du sténopé et l’objet, d’un côté ; ou la distance entre le sténopé et le film, de l’autre, nous réglons notre grandissement, donc notre cadrage après avoir bien poinré l’axe optique ; et comme nous avons mis notre film bien vertical, les lignes que nous arrivons à cadrer dans le format seront verticales, donc bien parallèles aux bords du film.
La condition est donc très simple : pour qu’une ligne verticale de l’objet soit projetée verticalement dans l’image, le plan du film ou du détecteur doit être vertical, quelle que soit l’orientation « droite-gauche » de ce plan, quelle que soit sa position, et quelle que soit la focale de l’objectif.
IV 2 Projection d’une façade, « distorsion en trapèze »
Avec un appareil photo dépourvu de mouvements, dès que l’on pointe l’axe optique vers le haut, le plan du film ou du détecteur penche vers l’arrière, il n’est plus parallèle à la façade photographiée, et la façade est projetée selon une « distorsion en trapèze » (figure 7b).
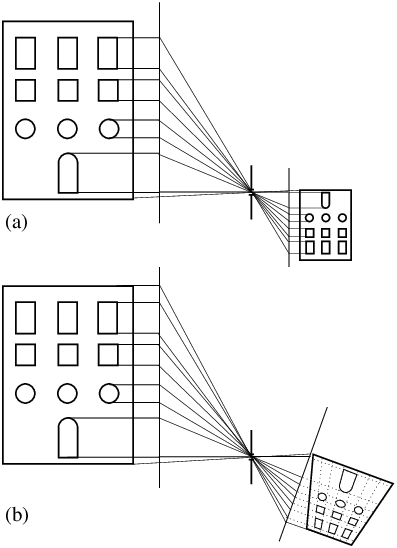 |
Figure 7: Modèle de la chambre à sténopé pour la distorsion en trapèze - (a) Avec décentrement vertical, plan de projection parallèle au plan de la façade - (b) En pointant un appareil dépourvu de mouvements vers le haut, le plan de projection devient incliné par rapport au plan de l’objet photographié, l’image est affectée d’une distorsion en trapèze qui n’est pas due à l’objectif.
Cette « distorsion » n’a évidemment rien à voir avec la distorsion d’un objectif, elle apparaît même avec un sténopé et même avec le meilleur des objectifs parfaitement corrigé de toute distorsion. C’est le simple résultat de la projection d’un plan-objet sur un plan-image qui ne lui est pas parallèle.
Notons également que lorsque que la projection se fait entre plans parallèles, un cercle tracé sur le plan de l’objet (figure 7a) se projette toujours comme un cercle, même si les rayons sont très inclinés.
Avec une prise de vue à la chambre, il suffit de laisser la plan du film vertical et de décentrer l’objectif vers le haut. Pour que l’image reste nette, il est nécessaire que la planchette porte-objectif reste verticale. Cette façon traditionnelle de procéder est limitée par le cercle d’image de l’objectif.
Dans un certain nombre de vues de Paris prises par Eugène Atget (1857 - 1927) [26], le décentrement dépasse la limite du cercle-image de l’objectif, un vignettage apparaît dans les coins supérieurs de l’image, mais les verticales sont bien verticales (figure 8).
 |
Figure 8: Lors de l’application d’un décentrement vertical, il arrive qu’on atteigne les limites du cercle d’image de l’objectif, comme dans cette photo d’Eugène Atget.
Aucune bascule n’est a priori nécessaire, sauf si l’on a recours au décentrement indirect (figure 9b).
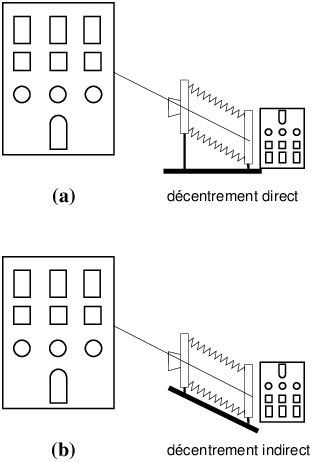 |
Figure 9: Avec un décentrement direct (a), le
rail reste horizontal, le corps arrière reste
vertical, l’axe optique est horizontal ; avec le
décentrement indirect (b), le rail pointe vers
le haut, le corps avant et le corps arrière sont
basculés du même angle de façon opposée pour que
l’axe optique reste horizontal et le plan du
film vertical.
Lors d’un décentrement indirect, le plan du film reste parallèle au plan de l’objet photographié, la planchette porte-objectif doit rester parallèle aux deux plans objet et image pour que la netteté soit bonne.
Si le cercle-image de l’objectif est insuffisant, on peut tenter, tout en gardant le corps arrière vertical, de pencher l’axe optique vers le haut pour éviter un vignettage. Cette façon de procéder est directement accessible avec les boîtiers de petit et moyen format équipés d’une optique à bascule et décentrement, lorsque qu’on est en butée du décentrement possible.
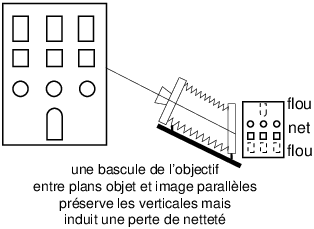 |
Figure 10: Pencher l’axe optique vers le haut tout en gardant le plan du film ou du détecteur bien verticaux, préserve les verticales en projection mais fait perdre la netteté.
Avec un objectif quasi-symétrique, la seule conséquence est la perte de netteté, il n’est alors plus possible de garder la netteté du haut en bas de l’image. Mais les verticales resteront verticales et parallèles dans l’image.
Avec un objectif grand-angulaire rétrofocus, comme ceux qui équipent les boîtiers reflex de petit et moyen format, pencher l’axe optique vers le haut tout en gardant le plan du film ou du détecteur bien vertical, non seulement fait perdre la netteté, mais fait, en plus, apparaître une distorsion particulière. Cette distorsion en « trapèze curviligne » n’existe pas avec les optiques quasi-symétriques, elle provient de ce que les images défocalisées, dans les rétrofocus, ne se projettent pas comme dans un sténopé (voir annexe 1, paragraphe VI).
IV 3 Projection d’une boîte parallélépipédique, vue en plongée
Après les bâtiments, passons aux prises de vue d’objets en studio. Nous ne regarderons de façon simplifiée et schématique que la question des verticales. Nous renvoyons pour plus de détails aux traités classiques de photo à la chambre [18], [19], [20], [21], [22]. La prise de vue photographique en studio, c’est un métier à part entière, cela ne s’explique pas en un court paragraphe avec deux ou trois tracés géométriques !
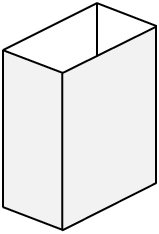 |
Figure 11: Une boîte parallélépipédique avec deux faces latérales opaques et une face supérieure transparente, représentée en perspective simplifiée. De nombreux objets de cette forme sont fréquemment pris en photo pour diverses sortes de catalogues. Autrefois, il était impensable que l’image imprimée dans le catalogue représente autre chose que des verticales bien verticales ! |
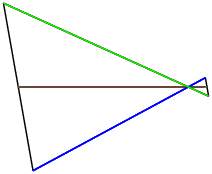
La boîte de la figure 11 sera posée sur un plan horizontal, et nous la prendrons en photo en légère plongée. De plus, nous tournerons légèrement la boîte pour que la face supérieure et deux faces latérales soient visibles.
Avec tous les mouvements à zéro, en pointant l’axe optique vers le bas pour une vue en plongée, les verticales de la boîte deviennent convergentes dans l’image (figures 12 et 13a).
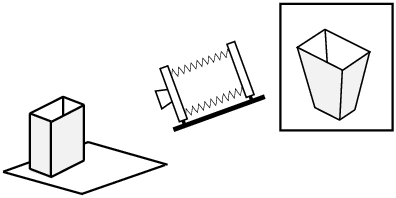 |
Figure
12: Image d’une boîte en plongée, tous
mouvements à zéro : les verticales convergent
(l’image
simulée est représentée redressée, sur le dépoli
de chambre elle se forme tournée de 180°).
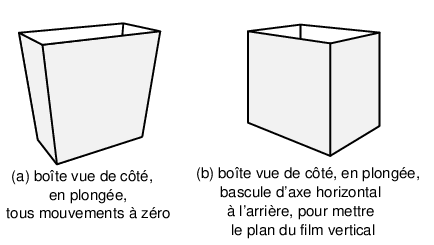 |
Figure
13: Tracé calculé pour la projection d’une boîte
parallélépipédique. (a) Vue en plongée, tous
mouvements à zéro. (b) Vue en plongée, après
avoir redressé le dos à la verticale.
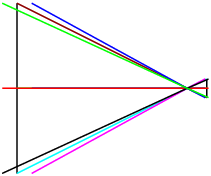
En redressant le dos pour que la plan du film soit parallèle aux arêtes verticales de la boîte, celles-ci se projettent verticalement dans l’image (figure 13b et 14).
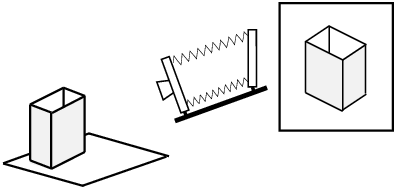 |
Figure 14: Image d’une
boîte en plongée, redressement du dos à la
verticale : les verticales de la boîte
redeviennent verticales dans l’image.
V Verticales et nutation lors de l’application de bascules croisées
Amies lectrices et amis lecteurs qui nous avez fait l’obligeance de nous suivre jusqu’ici, vous étiez déjà sensibilisés à cette question de la projection des verticales et de la distorsion en trapèze en photographie ; mais même si vous avez déjà une bonne connaissance et une bonne pratique de la prise de vue à la chambre, vous n’avez sans doute jamais entendu parler du phénomène de nutation.
Tout d’abord, une fois n’est pas coutume, le recours à un dictionnaire à l’entrée « nutation » est de peu d’intérêt, car le mot est principalement utilisé dans les cours de mécanique théorique. On verra dans l’annexe 2, paragraphe VII, la définition des trois angles de rotation dits « angles d’Euler » qui sont l’une des façons de déterminer l��orientation d’un solide dans l’espace.
Donc la nutation du gyroscope (annexe 2, paragraphe VII). n’a rien à voir avec ce qui nous concerne ici, si ce n’est la définition des trois angles de rotation combinés permettant de repérer la position angulaire du dépoli de chambre ou du porte-film dans l’espace (figure 15).
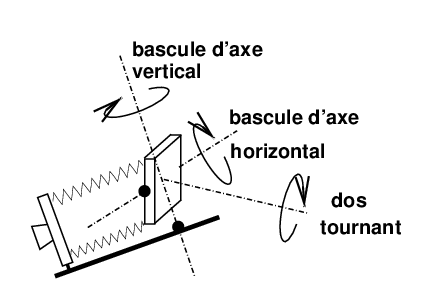 |
Figure 15: Les trois degrés de liberté de rotation pour un dos de chambre : les deux bascules croisées et la rotation du dos, ce dernier mécanisme n’existe que sur quelques chambres.
Nous allons présenter succinctement la question ; nous renvoyons pour une étude approfondie de la nutation qui peut apparaître lors de l’application de bascules croisées, aux exemples détaillés de prises de vue à la chambre, qui sont présentés dans l’article de Bernard Sulmon [27] publié sur https://www.galerie-photo.com.
Revenons à la prise de vue de
notre boîte (figure 14).
On pourrait s’arrêter là, car nos verticales
sont bien verticales, mais nous ne sommes pas
satisfaits de la façon dont les côtés de la
boîte sont projetés dans l’image, donc nous
voulons tourner droite-gauche le plan du film
pour changer cette projection.
Imaginons une chambre monorail avec une bascule d’axe horizontal, placée « au pied », à l’arrière, comme sur la figure 14. Lorsque nous redressons le plan du film à l’aide de cette bascule, l’axe vertical croisé de la 2e bascule se trouve aussi parfaitement vertical.
Et si nous tournons droite-gauche le plan de notre film selon cet axe mécanique bien vertical, comme sur la figure 16, en tournant suffisamment pour que le plan du film soit non seulement vertical mais parallèle à la face A de la boîte, selon les règles de projection rappelées précédemment, les images des arêtes de la boîte seront des lignes droites verticales (parce que le plan du film est vertical), avec en prime les arêtes horizontales de la face A projetés parfaitement horizontalement. De plus, l’image de la face A sera bien parallèle aux côtés du dépoli ou du film, parce l’axe mécanique vertical de la bascule « au pied » préserve la verticalité des côtés du film lors de la rotation.
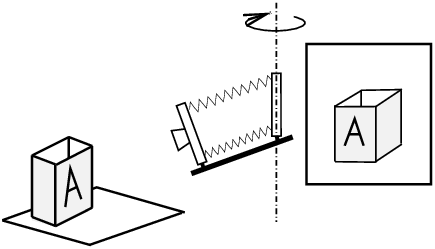 |
Figure 16: Lorsqu’on combine une bascule d’axe horizontal avec une bascule d’axe vertical, avec une chambre équipée de bascules « au pied », la deuxième rotation autour de l’axe vertical garde les rectangles projetés parallèles aux côtés du dépoli.
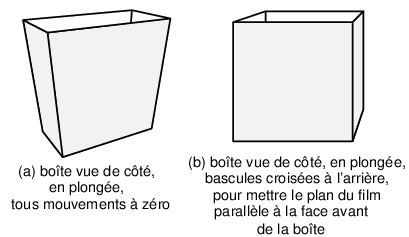 |
Figure 17: Tracé calculé pour la projection d’une boîte parallélépipédique. (a) Vue en plongée, tous mouvements à zéro. (b) Vue en plongée, après avoir redressé le dos à la verticale, et appliqué une deuxième bascule croisée pour mettre le plan du film parallèle à la face avant de la boîte.
Normalement, avec le sténopé, donc sans se préoccuper de la mise au point mais uniquement de la forme projetée, les réglages « géométriques » seraient terminés. Et on n’aurait jamais vu la nutation pointer son nez.
Mais nous entendons déjà l’une de nos lectrices ou l’un de nos lecteurs protester énergiquement : sa chambre, bien que monorail, a des bascules « à l’axe » à l’arrière, c’est à dire une espèce de fourche permettant de tourner le cadre de format autour de son milieu, et non pas des bascules « au pied » ! Nous commençons par la (ou le) féliciter, car elle (oui il) aurait pu n’avoir aucune bascule du tout à l’arrière, ou bien encore seulement des bascules « sur tige » de Linhof Technika ou de Mamiya Press, et nous aurions été bien en peine d’expliquer comment utiliser ces dispositifs de façon simple.
Donc nous avons une bascule « à l’axe » à l’arrière, comme sur la figure 18. Le rail est toujours incliné vers l’objet, pas de problème. Nous redressons le plan du film pour le mettre vertical, tout va bien, mais si nous voulons jouer de la bascule droite-gauche, celle-ci n’a plus son axe mécanique vertical !
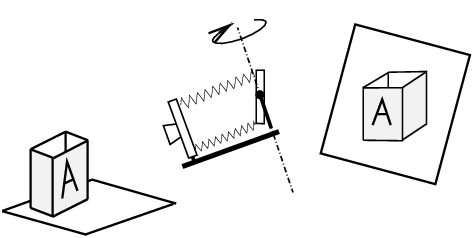 |
Figure 18: En combinant une bascule horizontale
« à l’axe » avec le deuxième mouvement croisé,
celui-ci n’est plus d’axe vertical après avoir
penché le rail, et l’image projetée n’est
parfois plus parallèle aux bords du dépoli,
c’est le phénomène
nutation.
Qu’à cela ne tienne, nous pouvons combiner la bascule droite-gauche avec la bascule « à l’axe », le plan du film finira bien par être vertical, mais ce sont les côtés du dépoli qui ne seront plus verticaux, et nos belles lignes droites et parallèles ne seront plus parallèles aux bords du film. Autrefois c’était bien casse-pieds ; voire franchement rédhibitoire.
Voilà l’effet de la nutation.
Et nous n’avons pas encore parlé de la gymnastique supplémentaire nécessaire avec le corps avant, équipé cette fois d’un de nos précieux objectifs, pour placer la zone de netteté exactement là où nous la voulons ! À cause de ce fichu M. Scheimpflug, dont les sténopistes se moquent joyeusement.
Nous renvoyons nos lectrices et nos lecteurs à l’étude détaillée qui est présentée dans l’article de Bernard Sulmon [27].
Bref, on imagine la déconvenue du professionnel d’autrefois, qui est très content de son cadrage, de son rendu de perspective et de sa netteté, et qui, au dernier moment, s’aperçoit que ses verticales-parallèles chèrement acquises ne sont plus parallèles aux bords du film. Évidemment, comme le cadrage était millimétré (le professionnel en question s’était endetté pour une chambre suisse-de-précision), lui suggérer que ce n’est pas bien grave, qu’il peut toujours massicoter le tirage final ou tourner un peu le plan-film dans le passe-vues de l’agrandisseur : vous aurez beau dire, tout cela n’est qu’une infamie, une provocation d’amateur inculte, un traficotage indigne d’un professionnel exigeant ; et vous vous ferez méchamment eng....er, à juste titre.
VI Annexe 1 : les grand-angulaires rétrofocus ne fonctionnent pas comme un sténopé !
La règle de projection classique permettant de conserver bien verticales et bien parallèles dans l’image les lignes verticales d’un édifice lorsqu’on travaille à la chambre, ne met pas a priori de condition très stricte sur l’orientation de l’objectif, tant qu’il est de formule quasi-symétrique.
La règle de Scheimpflug, en revanche, pour la mise au point entre plans inclinés, oblige à ce que le plan de l’objet, la planchette d’objectif et le film soient parallèles pour que l’image soit nette. On est cependant libre de basculer un peu l’objectif sans avoir de la distorsion en trapèze, mais en perdant la netteté parfaite, lorsqu’on veut absolument basculer l’objectif entre un plan objet et un plan image parallèles entre eux. Par exemple pour pointer l’objectif vers le haut de l’édifice (figure 19).
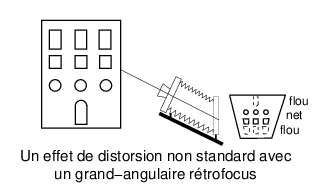 |
Figure 19 : Avec un objectif grand-angulaire rétrofocus, pencher l’axe optique vers le haut tout en gardant le plan du film ou du détecteur bien verticaux en vue de préserve les verticales en projection fait perdre la netteté et fait apparaître une distorsion en trapèze « non standard ».
De fait, et c’est très subtil, cette tolérance sur l’inclinaison de l’objectif n’est applicable qu’avec les objectifs de chambre qui sont presque tous de construction quasi-symétrique. Avec les grands angulaires rétrofocus pour petit et moyen format reflex, même si le plan de l’objet et le plan du détecteur sont parallèles, le fait de basculer l’axe optique fait non seulement perdre la netteté (effet classique) mais introduit une distorsion en trapèze supplémentaire qui n’existe pas avec les optiques symétriques ou quasi-symétriques.
Cet effet a été porté à la connaissance des lecteurs du forum http://www.galerie-photo.info par M. Jean-Paul Planchon, l’explication à été donnée par Fabrice [28].
La raison en est subtile ; lorsqu’on bascule l’objectif entre des plans objet et film qui sont parallèles, l’image qui se forme n’est plus une image nette mais une pseudo-image issue de la projection défocalisée du diaphragme sur le détecteur. Or les optiques grand angulaires rétrofocus ont la particularité d’avoir leurs pupilles qui ne sont plus situées au voisinage des points nodaux (ou principaux) comme dans les optiques de chambre. Cette particularité induit une distorsion supplémentaire en trapèze curviligne qu’il est très difficile d’appréhender sans faire une simulation par un tracé de rayons. Dans la pratique cet effet n’apparaît que très rarement, par exemple dans la configuration de la figure 19 entre plans objet et image parallèles, avec l’objectif qui pointe vers le haut.
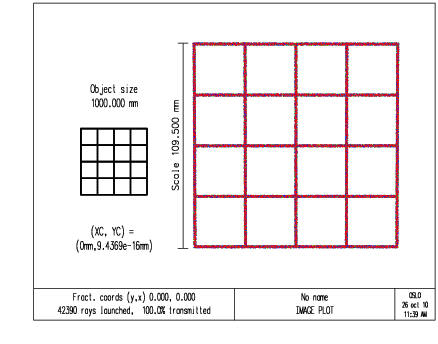
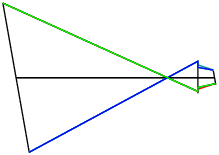
(a) Tracé de rayons entre plans parallèles, optique inclinée avec pupilles dans les plans principaux ; la simulation de ce système s’effectue avec un « objectif » purement mathématique, la « lentille aplanétique infiniment mince », diaphragmée en son centre.
(b) L’image d’une grille n’est pas déformée si on incline une optique symétrique dont les pupilles sont aux plans principaux. |
Figure 20: Dans les cours classiques de photo à la chambre, on apprend qu’on peut incliner un peu l’objectif entre un plan objet et un plan image parallèles sans que la distorsion en trapèze n’apparaisse : c’est vrai pour les optiques quasi-symétriques dont les pupilles sont proches des plans principaux.
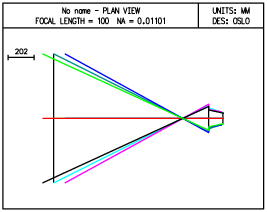
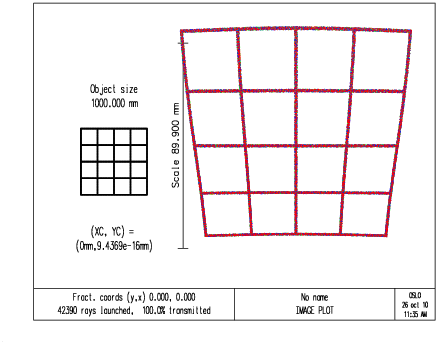
(a) Tracé de rayons entre plans parallèles, optique inclinée avec pupilles loin des plans principaux ; la simulation de ce système s’effectue toujours avec une « lentille aplanétique infiniment mince », mais cette fois diaphragmée en un point situé loin de son centre.
|
Figure 21: Effet de distorsion spécifique aux grands angulaires rétrofocus lorsqu’on penche l’objectif entre plan objet et plan image parallèles.
VII Annexe 2 : définition de l’angle de nutation au sens de la mécanique du solide
L’angle de nutation intervient en mécanique du solide dans le très beau problème des mouvements de la toupie en rotation rapide, reposant par sa pointe supposée infiniment pointue, sur un sol horizontal, et soumise à la pesanteur. Les calculs sont très complexes, mais, in fine, on montre que la toupie peut avoir son axe de rotation qui tourne lentement autour de la verticale (la « précession ») et que cet axe peut être l’objet de petites oscillations de bas en haut, la nutation.
Pour déterminer complètement la position d’un solide dans l’espace, il faut donner six paramètres :
-
Trois paramètres de position pour un point de référence du solide, dans un repère cartésien ce seront les coordonnées (x, y, z) de ce point ;
-
Trois angles de rotation définissant l’orientation du solide autour de ce point de référence, dans un repère tourné d’axes (Ox’, Oy’, Oz’).
L’une des façon de définir ces trois angles, c’est la combinaison dite des angles d’Euler, la notation consacrée dans les manuels français [29] est la suivante :
-
ψ l’angle de précession ;
-
θ l’angle de nutation ;
-
ϕ l’angle de rotation propre.
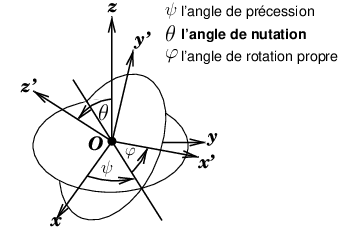 |
Figure
22: Définition des angles d’Euler : précession
ψ, nutation
θ,
rotation propre ϕ.
On retrouve également la nutation en mécanique céleste avec la précession des équinoxes et la nutation, qui affectent la direction de l’axe de rotation de la Terre au cours du temps [30].
Sources et Références
| [1] |
L’église Saint Pierre de Besançon, vue en contre-plongée sans décentrement,
|
| [2] |
Le temple Saint Martin de Montbéliard (FR-25) est sur la liste des rénovations prioritaires en Franche-Comté dans le cadre de la mission animée par Stéphane Bern pour la sauvegarde du patrimoine. https://soutenir.fondation-patrimoine.org/projects/ La prise de vue de cet édifice dans sa totalité depuis l’extérieur est délicate à cause du manque de recul possible pour le photographe. Il est donc tentant d’avoir recours à un ultra grand-angulaire, en contre-plongée, En revanche, cette vue frontale prise à l’intérieur de l’édifice depuis un point de vue un peu élevé (la chaire qui fait face à la tribune), ne présente pas de verticales inclinées, elle est parfaitement conforme à la tradition des photos d’architecture.
|
| [3] |
Au Nouveau Monde, pas de surprise, les murs et les colonnades penchent également sur Wikipédia !
|
| [4] |
Abbaye de Saint Savin sur Gartempe (FR-86), détail d’une fresque,
|
| [5] |
https://fr.wikipedia.org/wiki/Perspective_
|
| [6] |
https://fr.wikipedia.org/wiki/La_Cit%C3%A9_id%C3%A9ale_(Urbino)#
|
| [7] |
Véronèse, « Les noces de Cana » (1563) Le tableau de Véronèse :
|
| [8] |
https://fr.wikipedia.org/wiki/Contre-plong%C3%A9e Andrea Mantegna, faux oculus de la Chambre des Époux, Palais ducal, Mantoue, vers 1470
|
| [9] |
https://fr.wikipedia.org/wiki/L%27%C3%89glise_d%27Auvers-sur-Oise Le tableau de Van Gogh : Fichier:Vincent_van_Gogh_-_The_Church_in_Auvers-sur-Oise,_View_from_the_Chevet_-_
|
| [10] |
https://fr.wikipedia.org/wiki/Chambre_noire https://en.wikipedia.org/wiki/Camera_obscura#/media/
|
| [11] |
https://www.lunetoile.com/wp-content/uploads/2017/12/20171
|
| [12] |
Emmanuel Bigler, « Lumière, diaphragme et pupilles »
|
| [13] |
Emmanuel Bigler, « Angles de champ, focales, projections et rendu de perspective »
|
| [14] |
Le terme de rétrofocus fut introduit par l’entreprise Angénieux pour désigner une combinaison optique dans laquelle la distance entre la dernière lentille et le foyer est nettement plus longue que la distance focale de l’objectif. Les formules rétrofocus permettent de monter un grand-angulaire sur les appareils reflex dans lesquels la distance entre la dernière lentille et le foyer ne peut pas descendre en-dessous d’une distance minimale imposée par la présence du miroir de visée. Cette distance minimale est proche de la diagonale du format.
|
| [15] |
Par exemple, l’entreprise NWS Instruments, Lenzburg (AG-CH) propose (2020) un rétrofocus de 23 mm de focale, avec une distance baïonnette-foyer qui est celle des boîtiers Hasselblad V, c’est à dire 74,9 mm. Un tel objectif est de construction très dissymétrique, ses pupilles sont placées loin des plans principaux, le modèle géométrique de la camera obscura et du sténopé est très insuffisant pour expliquer le rendu de perspective dans ce genre d’objectif.
|
| [16] |
Emmanuel Bigler, Yves Colombe, « Glossaire des termes techniques de l’optique photographique » https://galerie-photo.com/glossaire-optique.html
|
| [17] |
Emmanuel Bigler, Yves Colombe, « Un objectif photographique n’est pas une lentille mince ! », (Première partie, introduction aux systèmes optiques centrés épais)
|
| [18] |
René Bouillot : Moyens et grands formats, Paul Montel (1971)
|
| [19] |
René Bouillot : L’objet et son image. Photographie industrielle et publicitaire, Paul Montel (1978)
|
| [20] |
Pierre Groulx : Photographie en grand format, Modulo, Québec (2001), ISBN 2891135059
|
| [21] |
(en anglais) Leslie D. Stroebel, View Camera Technique, 7-th Ed., Focal Press (1999), ISBN 0240803450
|
| [22] |
(en anglais) Harvey Shaman, The View Camera: Operations and Techniques, Amphoto Books (1992), ISBN 0817463755
|
| [23] |
Emmanuel Bigler, « La règle de Scheimpflug : un simple tracé de rayons pour lycéens ? », https://galerie-photo.com/demonstration-scheimpflug.html
|
| [24] |
Emmanuel Bigler, « Profondeur de Champ et règle de Scheimpflug : une approche simple »,
|
| [25] |
Emmanuel Bigler,
|
| [26] |
https://fr.wikipedia.org/wiki/Eug%C3%A8ne_Atget Laure Beaumont-Maillet, « Atget-Paris », Hazan (1992) ISBN 978-2-85025-294-5
|
| [27] |
Bernard Sulmon, « Nutation »
|
| [28] |
L’étrange distorsion supplémentaire en trapèze curviligne des objectifs grand-angulaires
|
| [29] |
https://fr.wikipedia.org/wiki/Angles_d%27Euler Angles nommés en l’honneur de Leonhard Euler (1707 - 1783) |
| [30] |
La nutation en mécanique céleste :
|
Voir les autres articles sur https://www.galerie-photo.com
Des questions ?
- Posez une
question sur le forum de
galerie-photo.info :
http://www.galerie-photo.info/forumgp
Dernière modification de cet article : décembre 2020
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||