[abonnement gratuit]
les auteurs
|
Emmanuel Bigler
est professeur (aujourd'hui retraité) d'optique et des
microtechniques à l'école d'ingénieurs de mécanique et des
microtechniques (ENSMM) de Besançon.
Il a fait sa thèse à l'Institut d'optique à Orsay
E. Bigler utilise par ailleurs une chambre Arca-Swiss
Mail

|
|
Yves Colombe, ingénieur
Ecole
Polytechnique
Docteur en physique atomique
En grand format utilise
une chambre Bender 4x5 pouces
yves.colombe@worldonline.fr

|
Télécharger cet article
au format pdf
In english |
Un objectif photographique n'est pas
une lentille mince !
Première partie, introduction aux systèmes optiques centrés épais
par Emmanuel BIGLER (1)
et Yves COLOMBE
(1)
Mél d'Emmanuel Bigler
Résumé
Nous commençons avec cet article une série qui traitera des optiques photographiques en tant que système optique
épais réel, en essayant d’aller plus loin que la représentation
traditionnelle simplifiée sous la forme d’une unique lentille mince
convergente. Ce premier article concerne les bases des systèmes optiques
centrés épais ; les articles suivants traiteront des questions de
photométrie, des réglages des diaphragmes, de l’importance des pupilles
et du problème de « raccordement panoramique » dans une optique épaisse.
D’autres articles traiteront de la profondeur de champ géométrique, de la
règle de Scheimpflug et de la diffraction dans un tel système épais
lorsqu’on ne peut plus le considérer comme une lentille mince.
La plupart des modèles expliquant la formation d’image dans une chambre
photographique grand format ne prennent en compte qu’une simple lentille
mince convergente. De façon assez étonnante, ce modèle est suffisant pour
expliquer la position et la grandeur des images, la profondeur de champ
et, dans une certaine limite, les effets de diffraction, la photométrie,
la règle de Scheimpflug et le rendu des perspectives. On se propose ici
de souligner l’intérêt du modèle de la lentille mince et de préciser dans
quelles circonstances photographiques il faut faire appel au modèle plus
élaboré du système centré épais.
Table des matières
I Introduction :
La chambre grand format, ou le retour à l’essentiel de
l’image
II Formules de conjugaison pour un système optique épais
III Conclusion
I Introduction : La chambre grand format, ou le retour à l’essentiel de
l’image
La formation d’une image à travers une lentille mince convergente est non
seulement à la base de la photographie, mais si on considère que l’œil
humain se compose d’un assemblage simple de dioptres sphériques, ce modèle
(en y adjoignant le dioptre sphérique) décrit également assez bien le
phénomène de la formation de l’image rétinienne. C’est donc un modèle très
simple basé sur l’association de deux dioptres sphériques (pour la
lentille) ou bien trois ou quatre dioptres avec des milieux d’indices
différents (pour l’oeil, selon la complexité du modèle optique retenu) qui
permet d’expliquer à la fois la formation d’image photographique et la
vision. Il semblait donc autrefois que tout photographe avait vraiment
besoin de connaître en optique au moins ce modèle de la lentille mince. Or
l’évolution technique des appareils photographiques au cours du XXe
siècle, du moins en ce qui concerne le matériel destiné au grand public,
tend à éloigner de plus en plus le photographe des rayons lumineux passant
à travers l’objectif et formant l’image sur un film classique ou sur un détecteur électronique. On pourrait donc penser qu’il
n’y a plus guère de raison pour le photographe du XXIe siècle, et
encore moins pour celles et ceux qui ne font plus de photos qu’avec leur
téléphone portable, de connaître ce qu’est une lentille, ni a
fortiori de connaître les lois de l’optique, ni de savoir en détail
comment se forment les images, puisque tout semble pris en charge
automatiquement.
L’utilisation d’une chambre technique, ou chambre grand format, nous oblige
à retrouver le phénomène de formation directe de l’image derrière
l’objectif, d’abord sur le dépoli puis sur un détecteur placé manuellement
au coup par coup, avec tout ce que cela comporte de rustique. L’image est
renversée, sur le dépoli elle est presque aussi sombre que celle d’un écran
à cristaux liquides, mais, heureuse surprise, comme disaient Pierre Dac et
Francis Blanche : « Et c’est en couleurs !»
On ne sait pas bien comment regarder cette image, certains s’évertuent à
vouloir la redresser ; on s’interroge sur la façon de cadrer. Les questions
de profondeur de champ semblent se poser de façon très différente par
rapport aux petits formats, dans certaines circonstances on vous parlera de
la règle de Scheimpflug et de bascules permettant « d’avoir une profondeur
de champ très grande » alors que d’autres prétendront que plus le format
est petit, plus la profondeur de champ est grande. Comment peut-on
expliquer tout cela ? Les très grands cercles d’image nette des objectifs
de chambre permettent grâce aux décentrements d’obtenir des perspectives
inhabituelles. Les lois de l’optique seraient-elles différentes d’un format
à l’autre, où le deviendraient-elles dès que c’est un soufflet qui prend
place entre l’objectif et le film ?
I 1 Le modèle de la lentille mince est-il réaliste ?
En pratique, et le lecteur s’en doute pour avoir déjà lu d’autres ouvrages
sur la photo, une bonne partie de ce qui vient d’être évoqué peut être
expliqué en se référant à un modèle d’optique géométrique (plus un tout
petit peu de diffraction) entièrement basé sur une seule lentille mince. Il
y a là un paradoxe qui est rarement pris en compte dans les ouvrages
traditionnels : en effet les ouvrages de photographie sérieux expliquent
avec force détails qu’il faut obligatoirement une combinaison de lentilles
de formes variées et des verres différents pour obtenir de bonnes images.
Les mêmes passionnés qui dénigreront un modeste triplet, qui feront la fine
bouche devant un prestigieux quatre-lentilles, seront les premiers à vous
tracer des diagrammes dans lesquels l’objectif se réduit à une seule
lentille mince convergente.
Alors, que faut-il penser de ce modèle de la lentille mince ? Toutes les
formules classiques utilisées par des générations de photographes (formules
de conjugaison, règle de Scheimpflug, photométrie, profondeur de champ,
diffraction,…) toutes ces formules qui sont allègrement recopiées d’un
ouvrage à l’autre, sans oublier bien entendu Internet, jusqu’à des sites
d’entreprises optiques ou photographiques renommées, seraient-elles toutes
fausses parce qu’aucun objectif ne se réduit à une seule lentille mince ?
I 2 Pourquoi cette série d’articles
Tel est le but de cette série d’articles : tout d’abord, montrer pourquoi
le modèle de la lentille mince unique est si fructueux pour décrire
quantitativement presque tout ce dont on aura besoin en
photographie courante ; mais également présenter les cas dans lesquels il
faut représenter le système optique centr������������������������������������������������ épais par quelque chose
de plus précis, sans pour autant devoir faire une révision déchirante de ce
qu’on sait déjà de la lentille mince.
Les formules classiques de la lentille mince restent utilisables presque
dans toutes les situations photographiques courantes, mais d’ailleurs qui
s’en sert sur le terrain ? L’un des intérêts de la chambre grand format
n’est-il pas, évidemment, de se laisser simplement guider par l’image qui
se forme manuellement sur le dépoli plutôt que se référer à un
formulaire, une calculatrice, un logiciel embarqué couplé à un pied à
coulisse électronique ?
Mais les utilisateurs de chambres grand format, du moins ceux dont on peut
lire les messages sur Internet, semblent être tellement épris de rigueur et
de précision qu’il apparaît tout aussi indispensable d’aller, d’abord pour
eux, certes, mais aussi pour tous les autres, un peu plus loin dans ce que
l’optique géométrique sait facilement expliquer à partir du modèle des
systèmes optiques centrés épais. Le cadre théorique est classique,
c’est celui de l’approximation des petits angles et des faibles
champs-image (approximation de Gauss).
On n’abordera pas ici les délicates notions du calcul des combinaisons
optiques ni la science de la correction des aberrations. Le mot d’ordre,
sauf exception dûment signalée, sera donc le suivant : les ingénieurs de
l’optique photographique depuis un siècle et demi consacrent tous leurs
efforts à réaliser en pratique des objectifs qui suivent
effectivement la règle de base de la formation d’image en optique
géométrique : tous les rayons d’un point de l’espace objet se coupent,
après réfractions multiples dans les lentilles, en un même point derrière
l’objectif qu’on appelle image géométrique. Dans un grand
angulaire moderne, les tracés de rayons très inclinés dans des lentilles
très bombées, en bord de champ, sont en réalité différents de ceux que l’on
peut déduire du schéma idéal pour un système épais représenté par ses
éléments cardinaux. Néanmoins, dans les optiques modernes très
bien corrigées de la distorsion –et ceci ne s’applique pas non plus aux
optiques de type « fish-eye »– on peut déterminer de façon correcte la
position et la grandeur des images dans toutes les optiques photographiques
actuelles en utilisant les règles de base des systèmes centrés épais et en
les extrapolant hors de l’axe optique ou pour des rayons très inclinés. Ce
qu’on peut dire tout simplement, c’est qu’un rayon rentrant dans l’objectif
réel (et dont on connaît les éléments cardinaux) ne ressort pas là où on
l’attend... mais rejoindra bien le plan image à l’endroit prévu.
Enfin, on trouvera sur ce site en accompagnement de cette série d’articles
un glossaire (ref. [1])
rassemblant, dans la terminologie française consacrée, l’essentiel
des notions abordées. Les termes écrits en caractères gras dans cet article
ont une entrée dans ce glossaire.
II Formules de conjugaison pour un système optique épais
II 1 Plans principaux H et H’
Il faut attaquer d’emblée par ce qui est peut-être le plus délicat, c’est à
dire la représentation des éléments cardinaux d’un système
optique centré [2, 3]. Partant de la formation de l’image et
de la relation objet-image dans une lentille mince convergente, on peut
montrer que les relations analogues pour une optique photographique épaisse
se déduisent assez simplement en introduisant l’écart HH′ appelé
interstice entre les plans principaux
(figure 1). Traditionnellement on appelle H et H′
l’intersection des plans principaux avec l’axe optique, ou points
principaux . Il n’est pas impossible de voir dans la lettre H la trace
originelle des très germaniques Hauptpunkt, Hauptebene que vous retrouverez dans les ouvrages d’optique
[4] et les spécifications techniques en allemand.
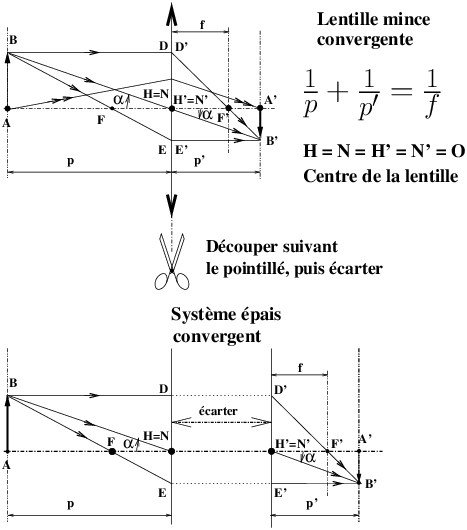
| Figure 1: Comment on passe de la lentille mince au système épais |
Partons de la correspondance objet-image dans une lentille mince
(figure 1) et découpons par la pensée le système en
passant par le milieu de la lentille : O = H = H′. Écartons l’espace
objet de l’espace image d’une distance HH′ sans modifier le tracé des
rayons en entrée et en sortie.
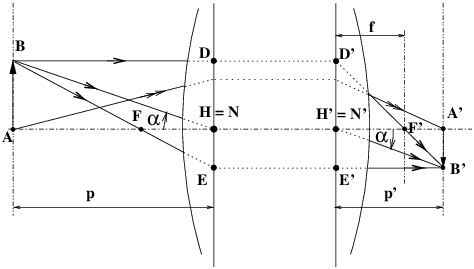
| Figure 2: Tracé symbolique des rayons à l’intérieur d’une optique épaisse |
On ajoute conventionnellement sur le tracé (figure 2) des pointillés
qui complètent les rayons à l’intérieur du système, ces pointillés ne sont
pas des rayons lumineux et n’ont pour but que de rappeler que la position
en hauteur d’un point tel que D en entrée se retrouve sur son homologue
D′ en sortie. Les points principaux sont conjugués l’un de l’autre, c’est
à dire que H′ est l’image de H ; c’est un peu difficile à comprendre
car on ne peut pas toujours avoir accès à ces points. On dit que pour les
plans principaux le grandissement transversal est égal à
un parce que les distances mesurées verticalement HD et H′D′ sont
égales, et du même côté de l’axe, pour le points D et son image D′ ;
ces points sont conjugués également.
Lorsque l’objectif travaille dans l’air, ce qui est le cas le plus fréquent
en photographie, les indices de réfraction du milieu d’entrée et
de sortie sont identiques, et dans ces conditions les points
principaux H et H′ sont confondus avec les points nodaux
N et N′ du système qui ont comme propriété particulière de conserver
l’angle α d’inclinaison du rayon entrant en N et sortant en
N′ (figure 2).
Nous obtenons ainsi un tracé qui n’est autre que l’épure d’un
système épais, pour lequel les formules de conjugaison sont
analogues à celles de la lentille mince :
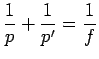 (1) (1) |
simplement, il faut compter les distances p et p′ à partir des plans
principaux respectifs : compter p à partir de H (pour l’espace objet),
et p′ à partir de H′ (pour l’espace image).
La formule (1) est connue en France sous le nom de
Formule de Descartes, elle est écrite ici sous sa forme
simplifiée valable pour un système convergent dans lequel les quantités p
et p′ sont toujours considérées comme des distances positives ; ce sont
celles qu’on utilise dans la pratique photographique.
Dans un objectif grand angulaire pour appareil reflex, le plan
principal image H′ peut être situé totalement en dehors du système
optique, entre la dernière lentille et le foyer. On expliquera plus loin
l’intérêt d’avoir ce plan principal H′ qui tombe très en dehors de
l’objectif. L’interstice, distance séparant H et H′, peut être très
important, mais il joue un rôle secondaire dans les applications
photographiques.
Bien noter, et cela se complique un peu, que les points H et H′ peuvent
être situés de manière « croisée » avec H de l’autre côté de H′ dans le
sens de parcours de la lumière (figure 3), on dit alors que
l’interstice HH′ (noté avec une barre dessus, c’est une
distance algébrique) peut être positif ou négatif. Dans le cas de la figure 1
la distance HH′ est positive car H’ est à droite de H, avec le
sens de parcours conventionnel de la lumière de la gauche vers la droite.
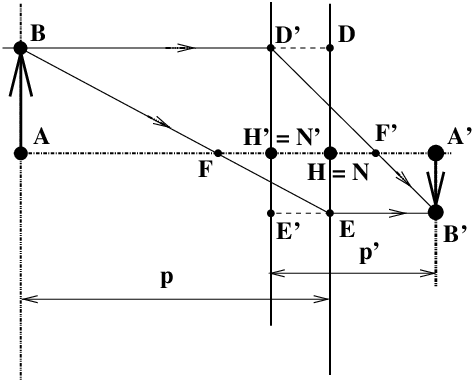
| Figure 3: Les plans principaux peuvent être croisés avec HH′<0 |
Dans le cas de la figure 3, on a HH′ négatif,
ce qui signifie simplement que H′ est à gauche de H ; cette situation
a priori un peu curieuse et difficile �� comprendre est en fait
courante, sans être une règle absolue, dans les formules
télé-objectif utilisés pour tous les formats lorsqu’on veut que la
longueur de l’objectif soit nettement plus courte que la distance focale.
Le but est de réduire l’encombrement total et le tirage mécanique
minimum requis en position infini - foyer. Ce qui compte en fait dans un
télé-objectif c’est que le point H′ soit en avant de la première
lentille ; la position du point H n’est pas ce qui importe le plus.
Dans le cas général, la formule de Descartes s’écrit avec des
distances algébriques ; on écrira par exemple dans le cas de la
figure 3 : HA < 0 H′A′ > 0 pour la
formation d’images dans une optique photographique.
Les points A et A′ sont à la verticale des points B et B′ sur
l’axe, exactement comme dans le tracé de rayons et les formules de
Descartes de la lentille mince. Les formules algébriques seront valables
de façon très générale pour tous les systèmes centrés, même les systèmes
divergents (par exemple un doubleur de focale) et pour toutes les
positions des objets et des images, sous la forme :
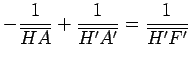 (2) (2) |
Dans l’équation générale (2), la quantité H′F′ est la
distance focale image du système épais ; pour un système
fonctionnant dans l’air, on a la relation :
H′F′=−HF si les milieux d’entrée et de sortie ont
les même indices de réfraction. Il suffit donc de définir une seule
distance focale qui est positive pour une optique photographique,
qui est un système optique convergent et que nous appellerons pour
plus de simplicité f ; en toute rigueur, il faudrait introduire la
distance focale image f′ et noter :
|

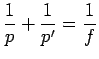 (1)
(1)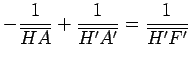 (2)
(2)