|
|
||||||||||||||||||||||||||||||||||||||||||||

les auteurs
|
Glossaire des termes techniques
|
|||||||||||||||||||||||||||||||||||||||||||
| Gα = α′/α (1) |
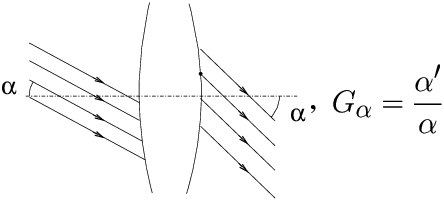 |
Figure 1: Système afocal et grossissement angulaire Gα
On ne peut pas former l’image d’un objet lointain sur un film ou un capteur avec un tel système, c’est pourquoi tous les objectifs photographiques ont une distance focale nominale. Une lunette astronomique ou terrestre, ou l’un des deux éléments monoculaires dans une paire de jumelles, est un système afocal lorsqu’il est réglé en position standard infini → infini. En pratique la plupart des instruments visuels renvoient l’image à environ un mètre de distance vers l’avant, ils sont donc très légèrement divergents. Ne pas confondre un système afocal avec un convertisseur de focale (15) pour appareil reflex (55) à optiques interchangeables.
3 approximation de Gauss
Théorie des systèmes
optiques centrés (57)
qui rassemble en quelques formules et règles de tracés de rayons
tout ce qui est nécessaire pour la construction de la position et de
la grandeur des images (voir refs. [2]
et [4]).
Le modèle ne s’applique au départ qu’aux rayons peu inclinés et qui
passent très près de l’axe optique (4),
mais tous les systèmes centrés si complexes soient-ils se comportent
de façon analogue pour ces rayons-là, appelés
rayons paraxiaux (45).
Pour une optique photographique réelle, les tracés de
l’approximation de Gauss permettent dans les objectifs modernes bien
corrigés des aberrations (1)
et de la distorsion (20)
de trouver correctement la position et la grandeur des images en
extrapolant les tracés symboliques en dehors de l’axe ou pour des
rayons très inclinés.
Exception en photographie : les objectifs ultra grands angulaires de
type « fish-eye » couvrant 180 degrés et plus, où les règles de
construction des images sont particulières.
4 axe optique
L’axe optique d’un
système centré (57)
est une droite sur laquelle doivent être alignés tous les centres de
tous les dioptres (17)
sphériques du système. Cet axe est donc l’axe de symétrie de
révolution commun à tous les
dioptres sphériques constituant le système. Éventuellement
les dioptres peuvent être asphériques. En général quand on parle de
surfaces asphériques dans
les objectifs à usage photographique, on sous-entend que ces
surfaces ont un axe de symétrie de révolution confondu avec l’axe
optique. Ce n’est pas toujours le cas : par exemple dans les
anamorphoseurs de cinéma, il y a des lentilles cylindriques et des
prismes ; un anamorphoseur de cinéma associe des systèmes centrés et
des systèmes sans axe de symétrie de révolution. L’analyse des
dioptres asphériques, même à symétrie de révolution, sort du cadre
des conditions de l’approximation de
Gauss (3).
Une rotation d’un système optique centré autour de son axe optique
qui est un axe de symétrie de révolution du système ne produit aucun
changement dans l’image.
5 cardinaux (points, éléments)
Voir : éléments cardinaux (22).
6 centré (système)
Voir : système optique centré (57).
7 centre optique
Le centre optique
n’est défini
que pour une lentille épaisse simple (refs. [2]
& [5]).
C’est, pour une lentille épaisse unique, l’image donnée du
point nodal (44)
objet N par le premier
dioptre (17)
(figure 2).
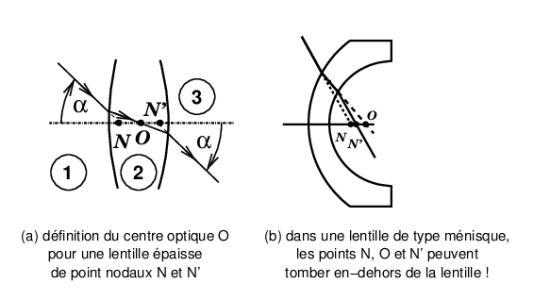 |
Figure 2: Définition du centre optique O pour une lentille épaisse simple de points nodaux N et N'
Soit une lentille épaisse de points nodaux (44) N et N′. Un rayon incident venant du milieu (1) pointe vers N sur l’axe et se réfracte sur le premier dioptre en passant par O qui est l’image de N dans le milieu (2). Le point O n’est pas nécessairement à l’intérieur du verre, si la lentille a une forme de ménisque (41) (figure 2b). Le rayon se réfracte ensuite à travers le deuxième dioptre et semble provenir de N′, qui est l’image de N donnée dans le milieu (3) par l’ensemble des deux dioptres formant la lentille. La propriété des points nodaux (44) est que l’angle d’inclinaison α pour tout rayon passant pas N et N′ est identique en entrée et en sortie.
On lit parfois sur Internet le terme de « centre optique d’un objectif ». Cette notion n’a pas de sens. Dans un système optique complexe formé de l’assemblage de plusieurs lentilles, on peut bien entendu construire les images successives du point nodal (44) objet N en progressant à travers les dioptres (17) du système ; la dernière image étant le point nodal image N′ donnée par le dernier dioptre. Il y a autant d’images intermédiaires du point nodal objet N que de dioptres (moins 1). Toutes ces images sont situées sur l’axe optique (4), elles sont parfois réelles, parfois virtuelles (42), mais ne jouent pas de rôle particulier en photographie. Si l’une de ces images est réelle, et qu’elle tombe dans l’air (mais pas forcément à l’intérieur de l’objectif), alors à cet endroit – s’il est bien choisi pour ne limiter que la luminosité et pas le champ – on peut placer le diaphragme d’ouverture (16) ce qui entraîne que les pupilles (54), c’est à dire les images du diaphragme données par le bloc optique avant et le bloc optique arrière seront placées aux plans principaux (51). Cette disposition, pupilles placées aux plans principaux, est réalisée, par exemple, dans les objectifs parfaitement symétriques dont le diaphragme est placé au centre de symétrie.
En conclusion, cette insistance à vouloir absolument chercher un « centre optique » à un objectif, provient de l’omniprésence du modèle de la lentille mince convergente diaphragmée en son centre et du sténopé pour expliquer la formation des images photographiques.
La plupart du temps, l’expression dénuée de sens « centre optique d’un objectif » est employée sans justification :
-
soit pour désigner le point nodal image N′ (identique au point principal H′ pour un objectif travaillant dans l’air) à cause des propriétés de stationnarité de l’image d’un objet lointain lorsqu’on tourne l’objectif autour de ce point N′, le détecteur étant fixe par rapport au sujet (ref. [6]) ;
-
soit pour désigner (plus rarement) le milieu du segment NN′ ou HH′ à cause des propriétés de stationnarité de l’image en macrophoto (40), en configuration objet-image symétrique « 2f-2f » lorsqu’on tourne l’objectif autour du milieu de ce segment (ref. [6]) ;
-
ou bien encore, pour désigner la pupille d’entrée (54 - voir également ref. [7]), image du diaphragme donnée par le groupe optique antérieur à la position du diaphragme, pour assurer la constance des effets de parallaxe lors de la rotation de l’ensemble de l’appareil.
C’est en effet autour de la pupille d’entrée de l’objectif qu’il faut tourner l’appareil dans son ensemble ; objectif + détecteur, pour réaliser des panoramiques par assemblage d’images en évitant les problèmes des raccordements d’images impossibles dûs au changement de point de vue consécutif au déplacement de la pupille d’entrée (voir ref. [8]).
Or dans tous les objectifs photographiques à plusieurs lentilles construits depuis le XIXe siècle, pupille d’entrée, centre de symétrie (pour les formules symétriques) ou milieu du segment NN′, et point nodal image sont distincts ! La pupille d’entrée est le point qui définit le centre de projection ou le centre de perspective pour la formation de l’image (ref. [8]).
Bien entendu, dans une lentille mince diaphragmée en son centre, les points nodaux et la pupille d’entrée sont confondus au centre de la lentille mince. Mais il n’en est rien dans un système optique épais !
8 chambre de campagne
Chambre photographique légère, parfois
pliante, souvent en bois surtout dans les formats supérieurs au
9x12 - 4x5 pouces, héritière des premières chambres photographiques.
Certaines chambres de campagne permettent de replier la planchette
d’objectif derrière un abattant frontal qui rend l’appareil
facilement transportable sur le terrain.
Anglais : field camera, flatbed
view camera, folding view camera - allemand :
Laufboden Fachkamera (Großformatkamera).
9 chambre monorail
Chambre technique basée sur la fixation des
éléments sur un banc optique unique permettant la mise au point par
déplacement le long du rail et l’échange rapide d’accessoires. Les
chambres monorail, surtout celles servant en studio, sont le plus
souvent en métal. Par rapport aux chambres de campagne, leurs
possibilités de tirage ou de mouvements ainsi que leurs gammes
d’accessoires sont bien plus étendus, souvent au détriment du poids
et de la compacité.
Anglais : monorail view camera -
allemand : Optische-Bank Fachkamera
(Großformatkamera).
10 combinaison optique
Association de dioptres (17) plans, sphériques ou asphériques ; de miroirs plans, sphériques ou asphériques, permettant la formation d’images de haute qualité par correction poussée des aberrations (1). Une même combinaison peut être extrapolée à différentes focales par multiplication de toutes les dimensions par un même facteur d’échelle. D’où la classification des optiques de chambre par familles, les grands angles, les standards, les télé-objectifs, les apo-symétriques, etc… Pour une même focale nominale, on trouvera des combinaisons optiques très différentes selon qu’il s’agit d’un grand angulaire pour un autre format supérieur, d’un standard ou d’un apochromatique symétrique pour un format donné, ou d’une longue focale de type « télé-objectif » (58) couvrant un plus petit format.
11 conjugaison (formules paraxiales)
Connaissant la distance focale f d’un système épais et la position des foyers F, F′ et des plans principaux H, H′, on détermine la position des images par rapport aux objets soit par la formule de Descartes (avec origines aux plans principaux) soit par la formule de Newton (origines aux foyers). Si A et A′ sont deux points conjugués sur l’axe, on a les formules algébriques (19) suivantes :
- formule de Descartes
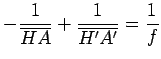 (2)
(2) - formule de Newton
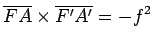 (3)
(3) - grandissement transversal
γ, et lien entre la position et la grandeur des
images :
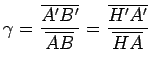 (4)
(4)Voir figure 3.
On notera que la formule de Descartes (équation (2)) et la formule du grandissement (équation (4)) ne sont pas utilisables pour un objet ou une image placés exactement aux plans principaux, les termes 1/HA et 1/H′ A′ tendant vers l’infini. Au voisinage de H et H′, on peut en revanche toujours utiliser la formule de Newton (équation (3)) ; on peut montrer que le grandissement γ tend vers 1 lorsque l’objet ou l’image s’approchent des plans principaux dont H et H′ sont les points sur l’axe optique.
À l’exception de certains tracés symboliques pour des objets situés au voisinage immédiat des plans principaux (51) pour lesquels les grandissements sont positifs (emplacements qui ne sont le plus souvent pas accessibles physiquement, mais on peut y renvoyer une image grâce à un autre système optique), le grandissement est en général négatif dans un appareil photographique entre un objet réel (42) (situé en avant de l’objectif) et son image réelle (42) sur le film ou le capteur (image qui se forme derrière l’objectif). Ce signe − du grandissement exprime simplement le fait que l’image réelle est renversée sur le dépoli.
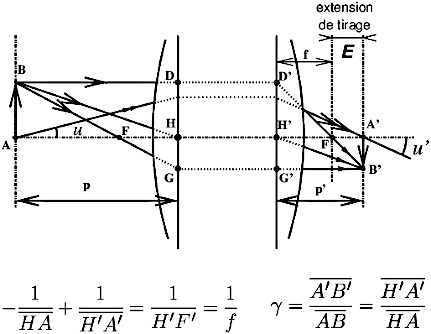
Figure 3: Épure d’un système centré, éléments cardinaux, grandissement transversal γ et extension de tirage E.
- lien entre le grandissement
transversal et le tirage : si |γ| désigne la valeur
absolue (positive) du grandissement, on a la
relation suivante :
E = |γ|× f (5) qui relie l’extension de tirage E qui est distance entre le foyer et l’image nette,
E = F′A′ = H′A′ − H′F′ (figure 3), mesurée à partir du plan focal, et le grandissement transversal γ.
On note souvent la valeur absolue du grandissement sous la forme |γ| = G = 1:10 ; G = 1:5 ; G = 1:2 ce qui signifie : G = 1/10 = 0,1 ; G = 1/5 = 0,2 ; G = 1/2 = 0,5
La distance totale A A′ entre l’objet et l’image est donnée de façon algébrique générale par l’équation (6) :
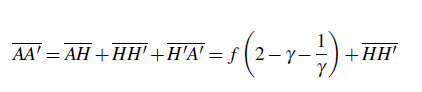 (6) (6) |
Dans le cas d’un objectif photographique avec focale f positive, objet réel et image réelle, on a γ < 1 ; si on pose G = |γ|, on a (équation (7))
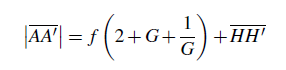 (7) (7) |
Lien entre le grandissement G et les distances A H et H′ A′ :
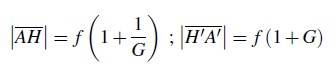 (8) (8) |
On notera bien que dans l’équation (7), l’interstice H H′ (39) peut avoir une valeur positive ou négative, même pour un système optique convergent (14).
La plus petite distance objet-image est obtenue en position objet-image symétrique « 2f-2f » (figure 4) ; on a, dans ces conditions : γ=−1 ; G=1 ; A H = 2f ; H′ A′ = 2f ; A B = − A′ B′.
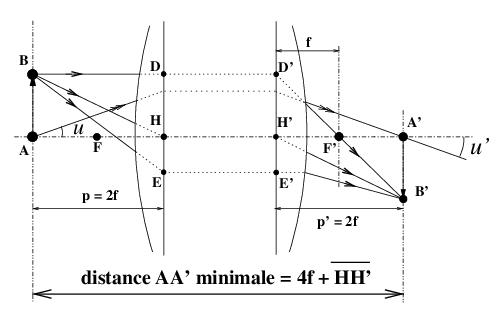 |
Figure 4: Position objet-image symétrique « 2f-2f » et distance minimale 4f + H H′
12 convergence
Inverse de la focale ; la convergence C s’exprime en dioptries par la relation :
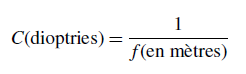 |
Un objectif photographique (système convergent (14)) de 100 millimètres de focale a une convergence de +10 dioptries. Une lentille ophtalmique divergente de -4 dioptries pour corriger la myopie a une focale de -250 mm. Lorsqu’on dit d’un viseur photographique qu’il est « réglé à -1 dioptrie » cela veut dire que l’image donnée du dépoli par ce viseur est renvoyée à une distance de 1 m en avant du viseur.
13 convergence (rapport de)
Voir : grandissement angulaire (31)
14 convergent (système)
Système optique pour lequel la distance
focale H′F′ (26)
est positive ; un tel
système est capable de former sur un film ou un détecteur
électronique l’image d’objets éloignés en « concentrant » dans
l’image l’énergie lumineuse émise par l’objet. Un
système divergent (21)
ne peut pas faire cela tout seul, mais il peut déplacer la position
et le grandissement des images photographiques s’il est associé avec
un système convergent.
Anglais : positive optical system -
allemand : Positiv Linsensystem.
15 convertisseur de focale
Système optique, pour appareils à objectifs interchangeables, qui s’intercale entre l’objectif et le boîtier et qui multiplie le grandissement transversal (11) par un facteur × 1,4 ; × 2 (doubleur) ; × 3 … sans changer le plan de mise au point. Les systèmes utilisés couramment en 24x36 et moyen format sont des systèmes divergents (21) (figure 5). Sans convertisseur, l’image se forme en A′B′. Après ajout du convertisseur derrière l’objectif, A′B′ devient un objet virtuel (42) dont l’image réelle (42) à travers le convertisseur se forme en A″ B″. Sur la figure 5, le convertisseur est représenté par une lentille mince divergente pour simplifier. Le facteur de conversion est égal au rapport des dimensions (A″B″)/(A′B′). L’épaisseur du convertisseur doit être égale à la distance A′A″ pour que l’image se forme toujours au même endroit au fond du boîtier.
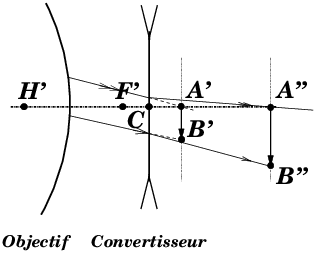 |
Figure 5: Principe du convertisseur de focale
En toute rigueur, ces dispositifs devraient s’appeler « convertisseur de grandissement ». En effet si l’objet est à l’infini, l’installation du doubleur, en doublant le grandissement, double effectivement la focale du système combiné. Mais si l’objectif de départ est équipé d’une rampe hélicoïdale de mise au point, et que la mise au point s’effectue par déplacement de l’ensemble de l’objectif, lorsque le doubleur est installé et qu’on tourne cette bague pour faire la mise au point sur un objet proche, la focale résultante du système change par suite de la variation de la distance H′C entre l’objectif et le convertisseur. La distance focale f de l’association de deux systèmes centrés se calcule facilement selon la formule de Gullstrand (équation (10) et ref. [12]) connaissant les focales f1 et f2 ainsi que la distance H′1H2 séparant les points principaux (52) des deux systèmes :
 (10) (10) |
Si l’écart
H′1H2
(H′C
sur la figure 5)
entre les deux systèmes change, la focale
f du système combiné change.
Anglais : teleconverter -
allemand : Telekonverter.
Ne pas confondre les convertisseurs de focale, groupes optiques divergents qui s’intercalent entre l’objectif et le boîtier, avec les compléments afocaux (2) (semblables à des monoculaires d’observation) qui se placent devant l’objectif, en particulier pour les appareils à objectif non interchangeable.
16 diaphragme
Ouverture limitant les faisceaux lumineux qui traversent un objectif. Dans les objectifs très anciens, on utilisait des diaphragmes à vannes, c’est à dire une plaque percée d’un trou circulaire qu’on coulissait entre les lentilles. La plupart des objectifs équipés d’un diaphragme d’ouverture ajustable utilisent le principe du diaphragme à iris (figure 6).

Figure 6: Exemple de diaphragme à iris sur un obturateur Compound
S’il est courant que le diaphragme soit placé entre les lentilles d’un objectif, dans le cas de l’objectif ménisque (41) de Wollaston (figure 17), un type très ancien, formé d’une seule lentille convexe-concave en forme de ménisque, le diaphragme est placé dans l’air, devant la lentille.
Selon l’endroit où est placé le diaphragme, cette ouverture toujours centrée sur l’axe optique (mais pas forcément circulaire), peut jouer le rôle de diaphragme de champ (limitant le diamètre visible de l’espace objet) ou de diaphragme d’ouverture (limitant la luminosité de l’image). Dans un objectif bien conçu, la bague de réglage des diaphragmes ne sert que pour régler la luminosité de l’image, le placement correct du diaphragme d’ouverture ne doit pas, en principe, limiter le champ.
Le placement correct du diaphragme est un point très important dans le calcul des combinaisons optiques, car l’endroit où le diaphragme est placé influe beaucoup sur les aberrations (1) et sur la distorsion (20).
Anglais : f-stop - allemand : Diaphragm.
17 dioptre
Surface de séparation entre deux milieux transparents d’indice de réfraction (38) différents, par exemple l’air et le verre à l’entrée d’une lentille ; une lentille simple se compose de deux dioptres. Dans l’oeil humain, l’essentiel de la convergence provient du premier dioptre sphérique formé par la cornée ; le cristallin, lentille déformable, fournit un appoint (indispensable) pour l’accommodation.
Exemples :
- dioptre plan : la surface de séparation entre les deux milieux est un plan ;
- dioptre sphérique : la surface de séparation entre les deux milieux est une sphère ;
- dioptre asphérique : la surface de séparation entre les deux milieux est une surface non sphérique ; dans les objectifs à usage photographique, cette surface présente souvent un axe de symétrie révolution confondu avec l’axe optique (4). Il existe aussi des dioptres cylindriques dans les lentilles cylindriques des anamorphoseurs de cinéma, et des dioptres toriques dans les lentilles ophtalmiques corrigeant l’astigmatisme.
18 dioptrie
Voir : convergence (12).
19 distance algébrique
Sur un axe orienté positivement de gauche à droite (figure 7), on dira que la distance AB est positive si B est à droite de A ; on a AB = − BA. On parle également de mesure algébrique.
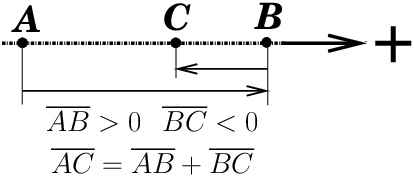 |
Figure 7: Définition des distances algébriques sur un axe orienté et relation de Chasles.
On a la version à une dimension de la relation de Chasles (équation (11), voir ref. [9]) :
|
|
Dans les tracés optiques des manuels français, on fait parcourir la lumière de gauche à droite ; espace objet à gauche, espace image à droite. Attention, cette convention n’est pas universelle, sur certaines vues en coupe des objectifs qui illustrent les documentations techniques des fabricants, il est courant de voir le dessin présenté avec la convention inverse, c’est à dire avec l’image à gauche et l’objet à droite.
Pour les axes verticaux on oriente positivement vers le haut ce qui permet de définir une valeur algébrique pour les grandissements. En photo courante, l’image est réelle (on peut la détecter sur un film ou sur un capteur) et le grandissement est toujours négatif (l’image est renversée).
20 distorsion
La distorsion optique est une déformation de
l’image, qui intervient lorsqu’on s’éloigne de
l’axe optique (4),
dans une conjugaison entre plans parallèles, pour laquelle
l’approximation de Gauss (3)
prévoit que l’image d’un objet qui est une grille à mailles carrées
est une grille à mailles carrées homothétique de l’objet (figure 8).
Voir également ref. [10].
Anglais : distorsion -
allemand : Verzeichnung, (optische)
Verzerrung.
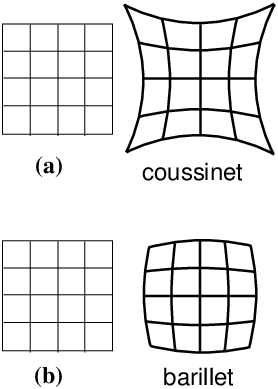 |
Figure 8: Distorsion optique en coussinet (a) ou en barillet (b).
21 divergent (système)
Système optique pour lequel la
distance focale (26)
H′F′
est négative comme dans une
lentille divergente. En associant plusieurs lentilles convergentes
avec des distances bien choisies entre elles, on peut néanmoins
obtenir un système divergent (voir figure 9
et ref. [2]).
L’association de lentilles divergentes en revanche ne permet pas
d’obtenir un système convergent.
Anglais : negative optical system -
allemand : Negativ Linsensystem.
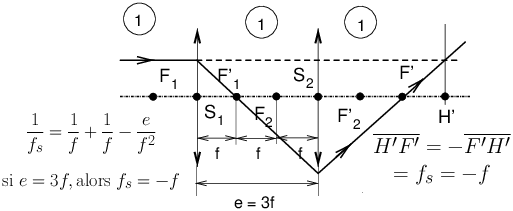 |
Figure 9: L’association de deux lentilles minces convergentes de même focale f, séparées par une distance 3f donne un système divergent de focale H′F′ = −f.
22 éléments cardinaux
Les éléments cardinaux d’un système épais sont les foyers (29, 30), les plans et les points principaux (51, 52), les plans et les points nodaux (43, 44). On ajoute parfois à cette liste des points cardinaux importants les points anti-nodaux et les points anti-principaux (voir ref. [2]). La connaissance de la position de ces éléments, qu’on calcule dans l’approximation de Gauss (3) connaissant les caractéristique du système (indices de réfraction (38) des milieux transparents traversés, courbures des dioptres (17), espacements entre dioptres) suffit à la détermination de la position et de la grandeur des images en partant d’objets donnés. Pour ce qui concerne les questions de photométrie (voir ref. [7]) et de profondeur de champ (voir ref. [11]), il faut de plus connaître la position des pupilles (54).
23 épure d’un système optique centré
Tracé géométrique symbolique plaçant pour un système centré les foyers, les plans principaux et nodaux ; pour une optique photographique dans l’air, on placera les foyers, les plans principaux, les sommets des lentilles en entrée et sortie, les plans d’appui mécanique (planchettes, montures à vis ou à baïonnette) et les pupilles.
Les fiches techniques de certains constructeurs donnent les positions des éléments cardinaux ainsi que les pupilles et leurs diamètres ; on peut également retrouver ces valeurs et redessiner l’épure d’un objectif à partir des données des brevets.
Voir des exemples d’une telle épure sur la figure 10, la figure 11 et la figure 22.
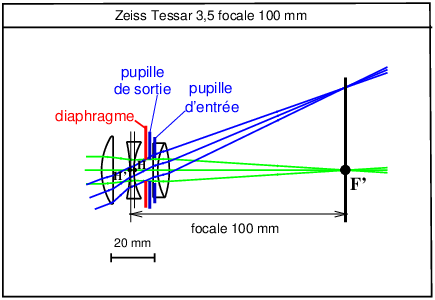 |
Figure 10: Épure de l’objectif Zeiss Tessar 3,5 - 100 mm calculée d’après les données d’un brevet. On remarquera que dans cet objectif, les plans principaux H et H′ sont « croisés », ainsi que les pupilles.
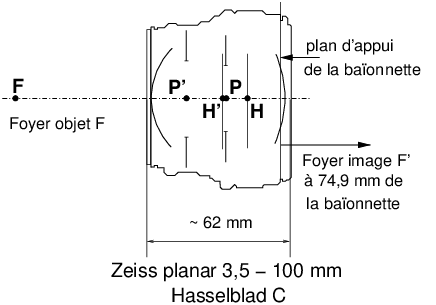 |
Figure 11: Épure de l’objectif Zeiss Planar 3,5 - 100 mm en monture Hasselblad C. On remarquera que dans cet objectif, comme dans le tessar précédent (figure 10) les plans principaux H et H′ sont « croisés », ainsi que les pupilles. Données d’après la fiche technique (ref. [13])
24 espace objet
Milieu transparent où est émise, en entrée, la lumière captée par l’appareil pour en faire une image. Dans ce milieu supposé homogène, les rayons se propagent en ligne droite. Si le milieu n’est plus homogène (si l’indice de réfraction varie le long du trajet des rayons) les rayons peuvent se propager sur des trajets courbes ; cette courbure explique l’origine des corrections à appliquer au pointé de la hauteur des astres mesurée au sextant au ras de l’horizon et le phénomène de mirage.
Le tracé symbolique des rayons ne se limite pas à des sources placées en avant de l’objectif, on peut aussi avoir des objets virtuels (42) placés derrière l’objectif, et qui, sur le plan des formules de conjugaison (11), se situent également dans l’espace objet.
Anglais : object space - allemand : Gegenstandseite
25 espace image
Milieu transparent où est reçue, en sortie, la lumière qui a traversé l’objectif et qui se focalise pour en faire une image. Dans ce milieu les rayons se propagent également en ligne droite. À chaque point de l’espace objet on associe un point de l’espace image par les formules de conjugaison (11).
Le tracé symbolique des rayons ne se limite pas à des images placées en arrière l’objectif, on peut aussi avoir des images virtuelles (42) placées en avant de l’objectif, et qui, sur le plan des formules de conjugaison (11), se situent également dans l’espace image.
Anglais : image space - allemand : Bildseite
26 focale (distance)
Distance
algébrique (19)
notée dans le cas général f′,
définie par f′ =
H′F′
qui sépare le plan principal image H′ du foyer image
F′
(voir figure 12).
Dans l’air, on a
H′F′
= −HF
pour tous les systèmes. Pour simplifier l’écriture, on appellera
f cette distance focale
H′F′
qui est positive pour tous
les objectifs photographiques.
Anglais : focal length -
allemand : Brennweite.
27 focaux (plans)
Plans perpendiculaires à l’axe optique et qui contiennent l’un ou l’autre des foyers F et F′ du système… du moins si on n’a pas affaire à un système afocal (2). Un faisceau de rayons émis par un point Fs du plan focal objet hors de l’axe sort dans l’espace image (25) sous forme de faisceau parallèle incliné. Un faisceau de rayons entrant dans le système, parallèles entre eux mais inclinés par rapport à l’axe ressortent en un point Fs′ du plan focal image ; on dit parfois que Fs′ est un foyer secondaire (voir figure 12).
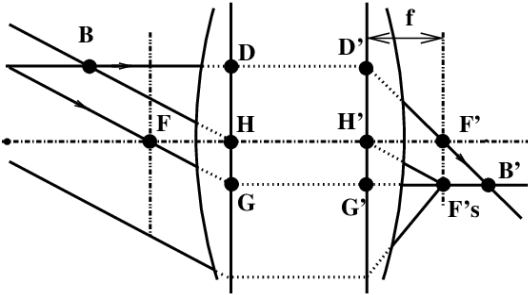 |
Figure 12: Plan focaux
28 formules de conjugaison
Voir : conjugaison (formules paraxiales) (11).
29 foyer image
Point de l’axe optique où se forme l’image
d’un faisceau de rayons parallèles à l’axe. Tout rayon entrant dans
l’objectif parallèle à l’axe sort en passant au foyer image.
On le note : F′ (voir
figure 12).
Anglais : focus, focal point -
allemand : Brennpunkt.
Attention : le foyer image
n’est pas l’image géométrique du foyer objet ! L’image du foyer
objet est renvoyée à l’infini sur l’axe sous forme d’un faisceau
sortant de rayons parallèles à l’axe.
30 foyer objet
Point de l’axe optique pour lequel l’ensemble
des rayons passant par ce point dans l’espace objet sortent
parallèles à l’axe dans l’espace image (figure 12).
On le note : F.
31 grandissement angulaire, rapport de convergence
Le grandissement angulaire (voir figure 13 et ref. [2]) Ga appelé également rapport de convergence est le rapport des angles Ga = u′/u formés par des rayons coupant l’axe au niveau d’un objet A (angle u) et de son image A′ (angle u′). Si l’objet et l’image sont dans le même milieu transparent, on a la relation entre Ga et le grandissement transversal γ (11) :
| Ga × γ = 1 (12) |
L’équation (12) est une conséquence de la relation de Lagrange-Helmholtz (voir refs. [2] et [4]) dans le cas de milieux d’entrée / sortie identiques.
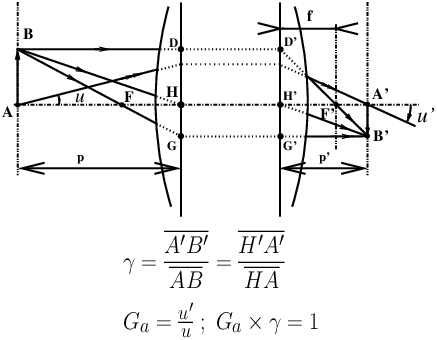 |
Figure 13: Grandissement transversal γ et grandissement angulaire
(appelé également : rapport de convergence) Ga
32 grandissement longitudinal
Soit A1A2 un petit segment (|A1 A2| ≪ |H A1|) de l’axe optique portant deux points-source A1 et A2. Soient A′1 et A′2 leurs images (figure 14). Le grandissement longitudinal γL est défini par :
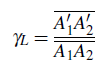 (13) (13) |
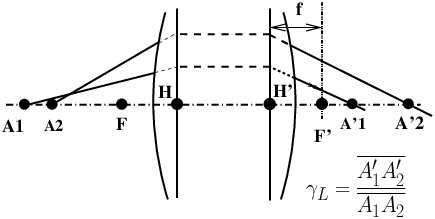 |
Figure 14: Grandissement longitudinal γL
Lien entre le grandissement longitudinal γL et le grandissement transversal γ (voir ref. [2]) :
En général, l’image d’un élément de volume par un système centré est comprimée (si |γ| < 1) ou dilatée (si |γ| > 1) dans le sens longitudinal. L’exception est le cas où |γ| = 1 ; c’est le cas de la position objet-image symétrique « 2f-2f » où γ = −1 ; dans ces conditions on a |γ| = |γL| = 1 et l’image volumique d’un petit objet est, dans les trois dimensions de l’espace, parfaitement fidèle à l’objet, à l’échelle 1.
33 grandissement pupillaire
Rapport des diamètres (diamètre de pupille de sortie) / (diamètre de pupille d’entrée).
Lorsque le grandissement pupillaire n’est pas égal à l’unité, les pupilles (54) ne sont pas placées dans les plans principaux (51) (voir figure 22 et ref. [7]).
34 grandissement transversal
Voir : conjugaison (formules paraxiales) (11).
35 grossissement (angulaire)
On définit le grossissement angulaire Gα pour un instrument visuel afocal (voir figure 1) en traçant un faisceau de rayons parallèles qui coupent l’axe optique en entrée en faisant un angle α avec l’axe ; en sortie les rayons sont parallèles et coupent l’axe en formant un angle α′. Le grossissement angulaire Gα est égal au rapport des angles α′ / α.
Gα étant un rapport d’angles, on peut définir ces angles dans l’unité que l’on veut, en radians ou en degrés du moment que les deux sont exprimés dans la même unité.
Pour un instrument tel qu’une loupe ou un microscope où les objets sont situés à distance finie, on définit le grossissement intrinsèque commercial Gic par le rapport entre l’angle sous lequel on voit l’objet à travers l’instrument et l’angle sous lequel on voit l’objet à l’oeil nu à la distance conventionnelle de 250 mm. Une loupe qui grossit 10 fois fait paraître une graduation millimétrique vue à travers la loupe sous le même aspect qu’une graduation centimétrique à l’oeil nu à 250 mm. Le lien entre Gic et la focale f d’une loupe est : Gic = 250/f(en mm). Une loupe 5x a une distance focale de 50 mm, une loupe de 100 mm de focale « grossit » 2,5 fois.
36 image géométrique
Lieu de l’espace image où se coupent les rayons issus des différents points de l’objet qui ont pu traverser complètement l’objectif. Dans l’approximation de Gauss (3), tous les rayons issus d’un point de l’espace objet se recoupent en un même point de l’espace image qu’on appelle image géométrique. Les systèmes optiques modernes et très bien corrigés des aberrations (1) réalisent très sensiblement cette propriété même pour des grands angles ou de grands objets, ce qui fait que dans un système optique épais réel, on peut se servir des formules de l’approximation de Gauss (3) pour déterminer la position et la grandeur des images.
37 Image réelle / virtuelle
Voir : objet / image - réel(le) / virtuel(le) (42).
38 indice de réfraction
Rapport sans dimension, noté n, de la vitesse de la lumière c dans le vide à celle Vn dans un milieu transparent. Dans un milieu transparent, et pour le domaine de la lumière visible, la vitesse de la lumière est toujours plus petite que dans le vide, on a donc n ≥ 1.
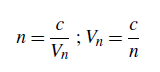 |
La vitesse de la lumière dans le vide vaut environ 300000 km/s. Le tableau suivant donne les valeur des indices de réfraction pour les milieux courants (selon ref. [14]).
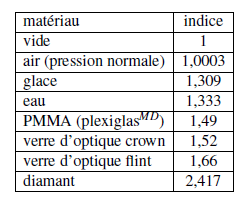 |
Tableau 1: Valeur des indices de réfraction pour quelques milieux transparents courants, selon ref. [14].
L’indice de réfraction intervient de façon fondamentale dans l’optique géométrique par la relation de Snell-Descartes (équation (16) et figure 15) :
|
|
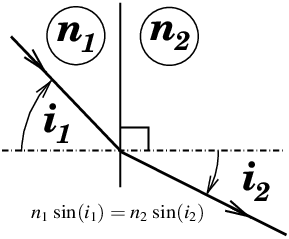 |
Figure 15: Réfraction de la lumière à travers un dioptre, loi de Snell-Descartes
39 interstice (optique)
Distance
algébrique (19)
HH′ entre les
plans principaux (51)
d’une optique épaisse.
Un interstice peut avoir une valeur positive ou négative.
Anglais : principal points
separation - inter-nodal distance - allemand :
Abstand der Hauptpunkte.
40 macrophoto
Prise de vue pour laquelle le grandissement (11) G est autour de 1, ou plus grand que 1.
41 ménisque (lentille)
Une lentille ménisque est formée d’une face bombée (convexe) et d’une face creuse (concave) (figure 16).
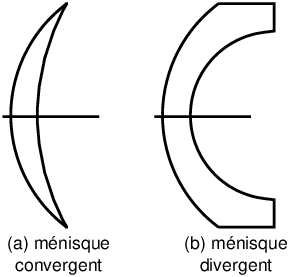 |
Figure 16: Ménisque convergent (a) et divergent (b)
Si le rayon de courbure de la face bombée est plus petit que celui de la face creuse (figure 16a), la lentille est convergente ; si c’est l’inverse (figure 16b), le ménisque est divergent.
Les lentilles ménisques sont utilisées dans de nombreux objectifs photographiques. Historiquement, l’un des premiers objectifs formés d’une seule lentille et d’un diaphragme est le ménisque de Wollaston (1804) (figure 17, voir ref. [15]).
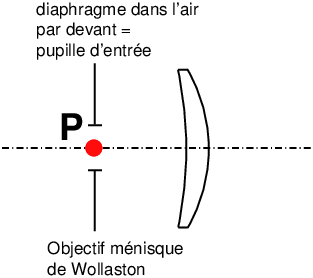 |
Figure 17: Objectif photographique ménisque de Wollaston (1804) (ref. [15])
42 objet / image - réel(le) / virtuel(le)
Objet et image doivent être compris dans le contexte de l’optique géométrique, comme :
- objet = source des rayons lumineux dans l’espace objet ;
- image = lieu où les rayons se croisent dans l’espace image, après traversée de l’instrument.
En fait, les formules de conjugaison générales (11) données par les équations (2) et (3) n’imposent pas que l’objet soit devant l’objectif, ou que l’image soit derrière ! Si l’objet est devant l’objectif, et que c’est un objet « ordinaire », du monde réel émettant ou diffusant la lumière, alors pour l’optique géométrique c’est un objet réel et on voit mal comment il pourrait être placé derrière l’objectif, sauf à faire fonctionner l’objectif à l’envers !
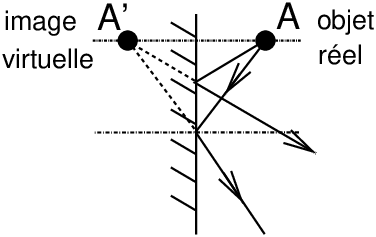 |
Figure 18: Image virtuelle A’ donnée d’un point source A par un miroir plan
En réalité, et aussi étonnant que cela puisse paraître, l’optique géométrique a prévu le cas où l’objet serait situé derrière l’objectif ! C’est ce qui se passe lorsqu’un autre système optique est réglé pour faire converger les rayons derrière l’objectif. L’objectif intercepte donc les rayons formés par le système optique qui est placé devant, et il peut parfois en donner une image réelle, comme si cet objet était réel ! Dans cette situation de l’objet placé « derrière l’objectif », on parle d’objet virtuel.
De la même façon l’image photographique qui se forme sur un dépoli de chambre, un film ou un capteur est une image réelle, on peut mettre un détecteur là où se forme cette image. Mais il existe également des image virtuelles, l’exemple le plus simple est l’image qui se forme dans un miroir plan (figure 18), et qu’on peut voir tous les jours dans sa salle de bains !
Les rayons réfléchis par le miroir plan semblent provenir d’un monde placé derrière le miroir, symétriquement du monde réel. On ne peut pas placer de détecteur là où se forme cette image, on l’appelle donc image virtuelle, mais on la voit de la même façon que si un monde réel symétrique était placé derrière une fenêtre ayant pour dimensions le cadre du miroir plan. Mais on peut facilement prendre une photo de cette image virtuelle pour la transformer en une image réelle.
Les figures ci-dessous (figures 19 et 20) résument ce qui se passe avec une lentille mince convergente ou divergente. Pour que l’objet soit situé derrière la lentille, il faut faire converger les rayons derrière la lentille avec un autre système optique placé par devant.
Dans le cas d’un système épais, les tracés des figures 19 et 20 restent valables, il suffit de décaler l’espace objet et l’espace image de l’interstice (39) H H′.
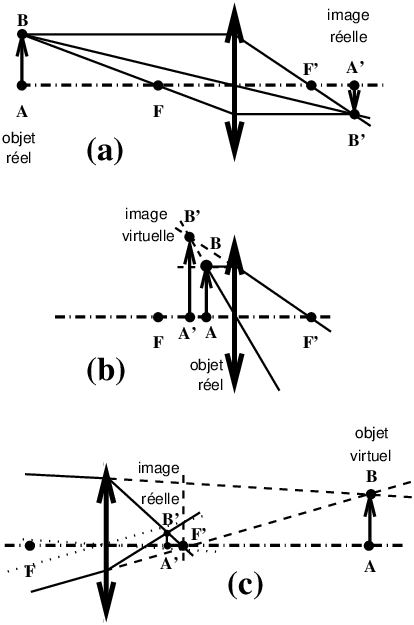 |
Figure 19: Construction des images pour un objet réel ou virtuel avec une lentille convergente : (a) objet réel et image réelle - (b) objet réel et image virtuelle - (c) objet virtuel et image réelle
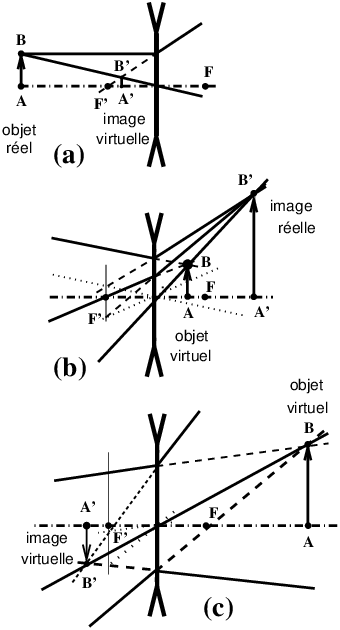 |
Figure 20: Construction des images pour un objet réel ou virtuel avec une lentille divergente(a) objet réel et image virtuelle - (b) objet virtuel et image réelle : c’est ce qui se passe dans un convertisseur de focale (15) - (c) objet virtuel et image virtuelle
43 nodaux (plans)
Couple de plans conjugués situés perpendiculairement à l’axe optique et passant par les points nodaux (44) correspondants. Pour une optique photographique utilisée dans l’air, les plans nodaux sont identiques aux plans principaux (51).
44 nodaux (points)
Couple de points conjugués, N et N′ sur l’axe optique pour lesquels le grandissement angulaire (31) ou rapport de convergence (31) Ga (figure 13 ) est égal à +1, c’est à dire que tout rayon passant par N en entrée ressort en coupant l’axe en N′ en étant parallèle au rayon d’entrée. Pour une optique photographique utilisée dans l’air, les points nodaux sont identiques aux points principaux, N=H ; N′ = H′.
Une propriété importante du point nodal image
N′=H′
est qu’une petite rotation de
l’objectif autour de N′
ne déplace pratiquement pas l’image d’un objet lointain qui se
formerait sur un écran fixe placé à proximité du plan focal.
On suppose ici que les objets dont on forme l’image sont situés très
loin de l’appareil, cas classique en photo de paysage panoramique.
Cette propriété de stationnarité de
l’image est mise à profit dans les appareils panoramiques à
tambour rotatif pour lesquels le film est fixe par rapport au
paysage (ou reste fixe par défilement rétrograde en synchronisme
avec la rotation de l’appareil en entier) et l’optique tourne par
rapport au paysage pour accumuler une succession de bandes minces
reconstituant le panorama. Le point nodal objet
N joue un rôle analogue si
l’optique est inversée… mais c’est une utilisation qui ne sert
pas en pratique.
Anglais : nodal point -
allemand : Knotenpunkt.
45 paraxiale (approximation)
L’approximation paraxiale est le modèle simplifié des systèmes centrés (57) qui ne traite que des rayons paraxiaux, c’est à dire les rayons lumineux proches de l’axe optique, et qui sont faiblement inclinés par rapport à l’axe optique.
Par exemple, avec une optique photographique à diaphragme très fermé, formant l’image d’un objet lointain, image dont on ne prend en compte que la partie centrale proche de l’axe optique, on peut considérer que l’on est dans les conditions de l’approximation paraxiale. La position et la grandeur des images sont alors données avec une bonne précision par les formules de conjugaison paraxiales (11) de l’approximation de Gauss (3).
46 plans focaux
Voir : focaux (plans) (27)
47 plans nodaux
Voir : nodaux (plans) (43)
48 plans principaux
Voir : principaux (plans) (51)
49 points nodaux
Voir : nodaux (points) (44)
50 points principaux
Voir : principaux (points) (52)
51 principaux (plans)
C’est un couple de plans conjugués parallèles entre eux et perpendiculaires à l’axe optique (4) pour lesquels le facteur de grandissement transversal (11) est égal à +1 (figures 3, 12). Dans une optique photographique quasi-symétrique, ces plans H et H′ sont très rarement accessibles physiquement. Ils sont situés dans ce cas particulier « géométriquement » l’intérieur de l’objectif sur l’épure du système (23, voir figures 10 et 11).
Dans le cas le plus général, ils peuvent être placés en dehors
des lentilles (voir sur la figure 23
l’exemple d’un télé-objectif (58)
pour lequel le plan principal image H′ est dans l’air, en avant de l’objectif !) et ils n’ont
qu’une signification symbolique permettant de déterminer la position
et la grandeur des images par un tracé de rayons géométrique. Le
plan principal image se trouve à l’intersection d’un rayon incident
parallèle à l’axe (de fait, son prolongement symbolique) avec le
rayon émergent correspondant ; le plan principal objet se trouve à
l’intersection d’un rayon émergent parallèle à l’axe avec le rayon
incident (son prolongement) correspondant (voir figures figures 3,
12).
Anglais : principal plane -
allemand : Hauptebene.
52 principaux (points)
On les note traditionnellement
H et
H′. Points de l’axe optique
situés respectivement dans le plan
principal objet (51)
(H) et dans le
plan principal image (H′) (51).
H et
H′ sont conjugués. Pour un
objectif travaillant dans l’air, les points nodaux (44)
sont confondus avec les points principaux.
Anglais : principal point -
allemand : Hauptpunkt.
53 proxiphoto
Abréviation pour : photographie rapprochée, avec des grandissements (11) G compris entre 0,1 et 1.
54 pupilles
On appelle pupilles les images du diaphragme (16) données respectivement dans l’espace objet par la partie antérieure de l’objectif (ce qui donne la pupille d’entrée) et dans l’espace image par la partie arrière de l’objectif (ce qui donne la pupille de sortie). La plupart du temps en optique photographique le diaphragme est situé entre les lentilles.
Il y a quelques exceptions comme le ménisque (41) de Wollaston (figure 17) et l’Imagon de chez Rodenstock où le diaphragme (de forme très spéciale) est placé dans l’air, en avant des lentilles. Il y a aussi des objectifs où le diaphragme est placé après la dernière lentille comme un Nikkor de 180 mm pour le 24x36.
Ce qu’on voit, en fait, lorsqu’on ferme le diaphragme et qu’on regarde une optique par l’avant ou par l’arrière, ce n’est pas le diaphragme lui-même mais les images de l’iris données par les deux moitiés de l'objectif. Il y donc a priori un facteur d’agrandissement ou de réduction de diamètre entre le diamètre réel du diaphragme et le diamètre de ses images, les pupilles (figure 21).
 |
Figure 21: Pupille d’entrée et pupille de sortie pour l’objectif Schneider-Kreuznach Télé-Arton de 360. Dans ce type d’objectif, la pupille de sortie a un diamètre plus petit que la pupille d’entrée, le grandissement pupillaire (33) est inférieur à 1.
En laissant ce diaphragme grand ouvert et en ajoutant soi-même un diaphragme assez fermé par devant ou par derrière l’objectif, on force les pupilles à s’identifier avec ce nouveau diaphragme ou son image donnée par l’objectif en entier. Les pupilles n’interviennent pas dans la position et la grandeur des images géométriques « nettes » au sens des formules de conjugaison paraxiales (11), en revanche elles sont très importantes pour le problème de la profondeur de champ (voir refs. [8] et [11]) où on prend en compte des images défocalisées.
La pupille d’entrée d’un objectif
est le point autour duquel il faut tourner un appareil ordinaire
(non panoramique) pour réaliser un raccordement panoramique d’images
avec le moins possible de défauts de parallaxe gênant le
raccordement d’une image avec sa voisine en bord de champ (voir
ref. [8]).
Anglais : entrance pupil, exit
pupil - allemand : Eintrittspupille, Austrittspupille.
55 reflex (appareil)
Appareil photographique pour lequel on regarde se former l’image à l’échelle 1 sur un dépoli en visant, via un système à miroir et un oculaire ou une loupe, soit à travers l’objectif de prise de vue (miroir mobile, reflex mono-objectif, en anglais : single-lens reflex, SLR - en allemand : Ein-aügige Reflexkamera) soit à travers un objectif de visée de même distance focale, très précisément appairé et jumelé à l’objectif de prise de vue (reflex bi-objectif, en anglais twin-lens reflex, TLR - en allemand : Zwei-aügige Reflexkamera)
56 rétro-focus (objectif)
Terme technique dû à la société française Angénieux pour désigner une classe d’objectifs de courte focale pour les caméras de cinéma, ainsi qu’une classe d’objectifs grand-angulaires pour appareils reflex à miroir dans lesquels la lentille arrière se trouve suffisamment en avant du plan principal image pour ne pas gêner le passage du miroir dans un reflex mono-objectif.
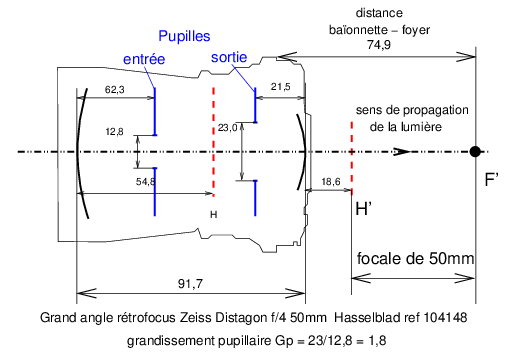 |
Figure 22: Épure de l’objectif Zeiss Distagon 50 mm en monture Hasselblad, modèle à groupes fixes des années 1970-1980. Dans ce type d’objectif développé pour les appareils reflex, le plan principal image H′ est dans l’air, loin derrière la dernière lentille qui ne risque pas de percuter le miroir-reflex. Données d’après la fiche technique (ref. [16]).
Ce type d’objectif est caractérisé par un grandissement pupillaire Gp (33) supérieur à l’unité, c’est à dire que le diamètre de pupille de sortie est supérieur au diamètre de pupille d’entrée, et les pupilles sont assez éloignées des plans principaux H et H′. Dans le cas de l’objectif Zeiss Distagon de la figure 22, le grandissement pupillaire Gp vaut 1,8.
57 système optique centré
Association de dioptres plans, sphériques ou asphériques, de lentilles minces ou épaisses présentant une symétrie de révolution autour d’un même axe optique (voir refs. [2] et [4]). On peut étendre assez facilement les propriétés de ces systèmes à une association de systèmes centrés couplés entre eux par des miroirs dans la mesure où les réflexions font correspondre entre eux les axes de différents sous-systèmes. Par exemple le système de visée totalement redressé d’un appareil reflex à pentaprisme associé à l’optique de prise de vue, au miroir reflex et à l’oculaire de visée se comporte, à un décalage latéral d’image près, presque comme un système centré unique.
Le modèle du système centré permet d’expliquer pratiquement toute la formation des images dans les systèmes photographiques.
Font exception certaines optiques spéciales comme les anamorphoseurs de cinéma, qui sont formés d’un assemblage de systèmes centrés, de prismes et de lentilles cylindriques.
58 télé-objectif
Formule optique en général de longue focale (26) par rapport à la diagonale du format, dans laquelle l’encombrement mécanique total est plus court que la distance focale ; de ce fait le point principal image H′ (52, 51) est situé dans l’air, en avant de la lentille frontale (voir figure 23).
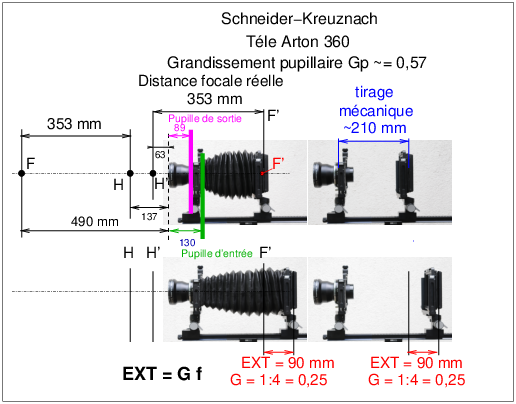 |
Figure 23: Télé-Arton de 360, position des éléments cardinaux sur l’objectif en situation réelle de prise de vue.
59 tirage mécanique
En tant que spécification intrinsèque d’un objectif, c’est la distance entre le foyer image F′ (29) de l’objectif et un élément mécanique de référence ; soit le plan d’appui de la planchette ou la monture du groupe optique arrière (objectif de chambre, voir figure 24) ; ou le plan d’appui de la baïonnette (appareils reflex (55) - voir figures 11 et 22). Ce qui est intrinsèque à l’objectif c’est la spécification de tirage mécanique lorsque la mise au point est faite en infini → foyer.
Dans le cas général, le tirage mécanique sera la distance entre
l’élément de référence mécanique et l’image. Entre la position
infini → foyer et la position « 2f-2f » (figure
4), le tirage doit augmenter d’une fois la distance focale.
Anglais : flange focal distance -
allemand : Anlagemaß.
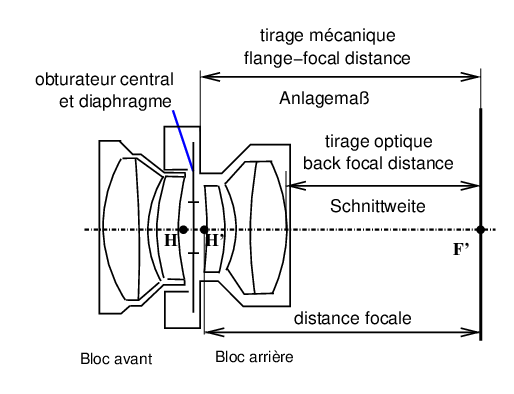 |
Figure 24: Tirage optique et tirage mécanique pour une optique de chambre montée sur obturateur central
60 tirage optique
En tant que spécification intrinsèque d’un objectif, c’est la distance entre le sommet de la lentille arrière et le foyer image F′ (29), voir figure 24. Dans un appareil reflex (55) mono-objectif à miroir mobile, la lentille arrière ne doit pas gêner le passage du miroir. Les solutions mises en oeuvre (parfois simultanément) sont :
- soit l’utilisation d’une formule optique rétro-focus (56) ;
- soit l’utilisation d’un miroir à cinématique complexe qui s’escamote sans percuter la lentille arrière.
Une optique
rétro-focus (56)
a un tirage optique infini → foyer plus long que la
distance focale (26) ;
voir figure 22.
Dans le cas général, le tirage optique sera la distance entre le
sommet de la lentille arrière et l’image. Exactement comme le tirage
mécanique, entre la position infini → foyer et la position
« 2f-2f » (figure
22), le tirage optique doit augmenter d’une fois la distance
focale. Il est possible d’utiliser sur un reflex mono-objectif des
objectifs dont le tirage optique en position infini → foyer est
insuffisant à condition de ne les utiliser qu’en
proxiphoto (53)
ou en macrophoto (40)
avec une distance H′A′ (figure
3) nettement plus longue que la distance
focale (26).
Anglais : back focal distance -
allemand : Schnittweite.
Références
Voir les autres articles sur https://www.galerie-photo.com
Des questions ?
- Envoyez à l’un des auteurs un
courrier électronique :
http://bigler.blog.free.fr/public/images/signature-eb-forums.jpg - Posez une question sur le
forum de galerie-photo.info :
http://www.galerie-photo.info/forumgp
Emmanuel Bigler et Yves Colombe 27 janvier 2021
Télécharger cet article en pdf
dernière modification de cet article : 2021
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||