|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

l'auteur
Télécharger cet
article au format pdf
Merci à Georges Laloire
|
Lumière, diaphragme et pupilles
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
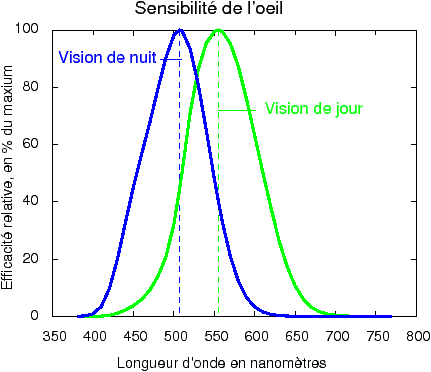
Figure 2 : Sensibilité de l’œil à la lumière visible, vision de jour et vision de nuit |
On dit couramment que la lumière visible s’étend entre 400 et 800 nm (de 0,4 à 0,8 µm) ; de fait, au-delà de 700 nm, la sensibilité est très faible, ce qui explique qu’il y a peu de films qui sont sensibles au-delà de 700 nm, du moins les films courants pour usage documentaire ou artistique dont le rendu doit être en accord avec la réponse de l’œil. Il existe bien entendu des films à sensibilité étendue dans le rouge, voire dans le proche infra-rouge ; mais les besoins en imagerie militaire ou scientifique, applications traditionnelles de ces films, sont aujourd’hui avantageusement satisfaits par les capteurs d’images silicium. Les posemètres et les capteurs d’images silicium ont en effet une sensibilité qui s’étend jusque dans l’infra-rouge, où elle peut même être meilleure que dans le visible ; d’où le filtrage « en bleu » des posemètres à élément silicium pour l’usage photographique dans le visible, et le filtre« infra-rouge » qui équipe les capteurs des appareils photo numériques courants.
En vision de nuit, un autre système de cellules rétiniennes très sensibles se met en place, avec une courbe de réponse qui est décalée vers le bleu. Les deux courbes ne sont pas tracées à la même échelle sur la figure 2, en vision de nuit, après un long temps d’accoutumance dans l’obscurité, l’œil est, dit-on, capable de détecter les photons pratiquement un par un !
Au vu de ces courbes, il est donc important que les posemètres tiennent compte de ces paramètres physiologiques ; un même nombre de photons rouges à 700 nm ne produira pas le même effet sur l’œil qu’un nombre identique de photons jaunes-verts à 550 nm. Néanmoins pour la suite de notre article, pour simplifier, il suffira de raisonner sur un nombre de photons reçus, en imaginant par exemple qu’ils tombent tous à la même longueur d’onde.
1.2 Formule photométrique fondamentale
Bien entendu on photographie toujours une scène dont l’étendue des luminosités est plus ou moins grande, avec de nombreux détails qui font tout le charme de la photographie, mais pour ce qui nous intéresse ici on va supposer qu’on photographie un simple mur gris.
Sans rentrer dans les détails d’un cours de photométrie ou de sensitométrie, on va admettre que pour que l’exposition soit correcte, il faut que chaque centimètre carré de film ou de détecteur silicium reçoive une certaine quantité totale de lumière, appelée lumination(unités : lux . secondes), égale au produit de l’éclairement reçu au niveau de l’image par le temps de pose. En termes de photons, la lumination est simplement le décompte du nombre total de photons reçus par mètre carré d’image pendant la pose (plutôt : par centimètre carré pour les formats de dimension courante !). En termes d’énergie ce sera la dose intégrée reçue par unité de surface, si par exemple le flux solaire est de 350 watts par mètre carré, intégré sur une seconde cela donne une énergie de 350 joules par mètre carré, soit 35 millijoules par centimètre carré.
La grandeur physique qui définit la « luminosité » du sujet s’appelle sa luminance. On lira dans l’annexe technique la définition précise de la luminance en tant que grandeur photométrique fondamentale. Pour l’instant il suffit de dire que tous les murs gris que l’œil perçoit avec le même ton de gris, qu’ils soient placés loin ou proches de l’œil, correspondent à la même luminance lorsqu’il sont éclairés par la même source large et lointaine, par exemple le soleil.
Pour savoir si un carton gris (éclairé par exemple au soleil par réflexion) a la même luminance que le mur, ou pour savoir si un négatoscope sur lequel un film gris est placé a la même luminance que le mur éclairé par le soleil, c’est très simple. On place le carton ou le négatoscope devant le mur et on regarde s’il est plus ou moins clair que le mur ! Si le négatoscope est de luminosité réglable, il peut exister un réglage particulier du négatoscope pour lequel l’impression visuelle est la même que celle du mur : dans ces conditions le négatoscope éventuellement recouvert d’un film gris aura la même luminance que le mur éclairé par le soleil.
Une propriété très remarquable de la photométrie classique, du moins dans le cas où le mur et le carton ou la source de type« négatoscope » sont « mats » ou « diffusants » (sources dites « lambertiennes », émettant la lumière de la même façon dans toutes les directions), est la suivante : quelle que soit la distance à laquelle on place le carton vis à vis du mur, lorsque le carton a la même luminance que le mur l’œil ne fait plus la différence entre le carton et le mur... La luminance pour un objet mat est donc intrinsèque à cet objet, elle est perçue de la même façon par l’œil quelle que soit la distance, du moins tant que l’objet n’est pas réduit un point. Pour un objet réfléchissant, brillant ou poli, les choses sont plus compliquées car la « luminosité » de l’objet dépend de l’angle sous lequel on l’éclaire. Il suffit de penser au fameux « point chaud » qui se forme lors d’une projection sur un support brillant pour comprendre que la luminosité dans ce cas n’est plus intrinsèque à l’objet réfléchissant seul mais qu’elle dépend aussi de la dimension et de la position de la source ainsi que de l’angle d’incidence et de réflexion des rayons d’éclairage.
|
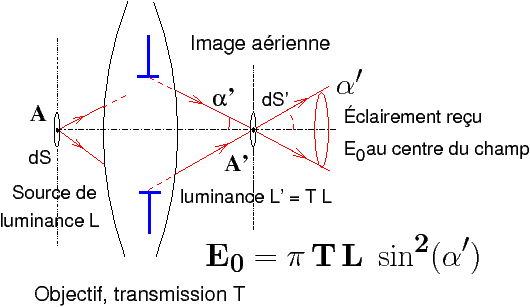
Figure 3 : Formule fondamentale de la photométrie pour un appareil photographique
|
Si on appelle L la luminance d’une portion de l’objet, par exemple le mur gris, le modèle classique photométrique (réfs. [6] et [7]) appliqué à une lentille mince convergente nous permet de déterminer l’éclairement E0 dans l’image du mur gris, (figure 3) au voisinage de l’axe optique, par la formule :
| E0 = π T L sin2(α′) (1) |
où
E0 est l’éclairement reçu dans le plan image, au centre du champ au niveau de l’axe optique ; le produit E0 × temps est la lumination qui permet de déterminer le noircissement du film ou le nombre de photo-électrons capturés par un pixel pendant la pose,
π = 3,141592..
T = facteur de transmission de l’objectif, liée à l’absorption et aux réflexions parasites, idéalement T=1 s’il n’y avait aucune absorption et aucune réflexion parasite,
L = la luminance de l’objet,
α′ le demi-angle sous lequel on voit, depuis le film, le diaphragme centré et placé tout contre la lentille mince.
On se reportera à l’annexe
technique pour voir d’où vient cette formule, ainsi qu’une
définition précise de ce qu’est la luminance, la grandeur
photométrique à la fois la plus importante et la moins intuitive à
comprendre.
Si a désigne le diamètre de ce diaphragme supposé idéalement
circulaire, et d la distance entre le diaphragme et l’image,
c’est à dire la distance entre la lentille mince et l’image (qui ne se
forme au foyer que pour les objets lointains), la formule fondamentale
de la photométrie devient, en calculant explicitement la valeur du sinus
carré :
| E0 = π T L (a/2)2 / | ⎛ ⎝ |
(a/2)2 + d2 | ⎞ ⎠ |
= π T L a2 / | ⎛ ⎝ |
a2+ 4 d2 | ⎞ ⎠ |
(2) |
On définit le nombre d’ouverture « vrai » par
| Nvrai ≡ 1 / | ⎛ ⎝ |
2 sinα ′ | ⎞ ⎠ |
(3) |
Ce qui permet d’écrire la formule photométrique de façon plus simple :
| E0 = π T L / 4 Nvrai2 (4) |
Comme un sinus est toujours plus petit que 1,
... du moins pour un système aplanétique fonctionnant dans l’air. En pratique on utilise la plupart du temps des objectifs dont le nombre d’ouverture est plus grand que 1, et on utilise une définition approchée du nombre d’ouverture par référence au diamètre de l’iris pour une lentille mince ou plus généralement par référence au diamètre des pupilles d’entrée et de sortie pour un système épais (voir plus bas au paragraphe 2.1).
Si on définit par Neff le nombre d’ouverture effectif approché défini par Neff = d/a, on trouve finalement la formule valable en toute généralité même pour un système épais :
| E0 = π T L / (1 + 4 Neff2) (5) |
Le point important dans cette formule (5), c’est que du côté objet, seule la luminance de la source intervient, la distance objet-appareil n’intervient pas, même la distance focale n’intervient pas directement. Ce qui explique que tous les objets de même luminance, exposés pendant le même temps de pose, vont donner sur le film la même lumination et donc le même noircissement local, ou le même nombre d’électrons par pixel (tant que le pixel reste plus petit que l’image de l’objet), et cela quelle que soit la distance à laquelle ces objets sont placés, du moment que la distance entre la lentille et le film ne bouge pratiquement pas ! (ce qui est le cas pour les objets lointains dont l’image se forme au foyer de l’objectif).
On lève ce paradoxe apparent de la façon suivante : si on éloigne l’objet en doublant la distance à l’appareil, son image voit son diamètre se réduire d’un facteur 2 environ derrière l’objectif, la quantité de lumière envoyée par l’objet, et qui rentre dans l’objectif diaphragmé va être divisée par quatre, mais l’image étant 4 fois plus petite en surface (l’objet étant 2 fois plus loin), l’éclairement qui est ramené à l’unité de surface ne va pas changer, on aura le même noircissement mais sur une plage plus petite de film. Seules les variations importantes de la distance objectif-film en macro-photo ont une influence sur la luminosité de l’image (voir plus bas a question du facteur de soufflet au paragraphe 1.6).
Dans le cas général d’un système épais, d va désigner la distance entre la pupille de sortie et l’image (voir plus bas la définition de la pupille de sortie au paragraphe 2.1), mais la formule (1) reste inchangée.
On remarquera que la formule photométrique fondamentale ne fait pas référence directement à la focale de la lentille mince, mais simplement à la distance entre la lentille (ou la pupille de sortie dans le cas général) et l’image.
Dans le cas où l’objet se situe très loin de la lentille, l’image se forme très près du foyer et on identifie alors d avec la focale f, le nombre d’ouverture effectif Neff devient égal au nombre d’ouverture classique N∞ = f/a, celui qui est gravé sur les échelles des objectifs et qui suppose sans le dire que l’image se forme au foyer parce que l’optique est réglée sur l’infini (le symbole ∞ est classiquement gravé sur les objectifs pour repérer la mise au point sur l’infini). Dans la suite on utilisera indifféremment N∞ ou N pour désigner le nombre d’ouverture tel qu’il est gravé sur les bagues des objectifs.
Dès que ce nombre d’ouverture devient plus grand que 2, la quantité 1 + 4 N2 peut être confondue avec N2 ; pour N=2, l’écart relatif d’éclairement entre la formule exacte donnant 17 et la valeur approchée 16 n’est que de 6% ce qui équivaut à une correction inférieure au dixième de cran de diaphragme, en photo c’est parfaitement négligeable. Sachant que les nombres d’ouverture effectifs Neff en proxiphoto sont toujours plus grands que N déterminé par la position infini-foyer, on voit qu’on peut sans crainte utiliser la formule approchée dans laquelle Nvrai est confondu avec Neff :
| E0 = π T L / (4 Neff2) (6) |
La lumination reçue sera donc proportionnelle à l’inverse du carré du nombre d’ouverture effectif. En réintroduisant la surface S = πa2/4 du diaphragme supposé circulaire on trouve finalement pour l’éclairement au centre du champ :
| E0 = T L S/d2 (7) |
Comme la plupart des diaphragmes ne sont pas circulaires, on déterminera en pratique une graduation de diaphragme en prenant pour le calcul du nombre d’ouverture, le diamètre d’un cercle de même surface que le polygone à côtés curvilignes habituel avec les diaphragmes à iris.
|
Figure 4 : La chambre grand format permet la visualisation immédiate de l’effet de l’ouverture du diaphragme sur la luminosité de l’image ; on notera que l’image sur le dépoli est plus sombre que l’image aérienne qui se forme directement derrière l’objectif, dépoli enlevé. Cette image aérienne, vue d’un œil humain ou d’un appareil photographique centré sur l’axe optique du premier objectif, semble limitée à un petit cercle de même dimension que l’ouverture du diaphragme ; mais elle est de même « luminosité » que la scène photographiée, c’est une conséquence de la loi fondamentale de conservation de la luminance dans une image aérienne. Pour compenser l’assombrissement dû au dépoli, on a volontairement surexposé les images pour mieux voir celles données par le dépoli. |
 |
1.3 Nombre d’ouverture et ouverture numérique
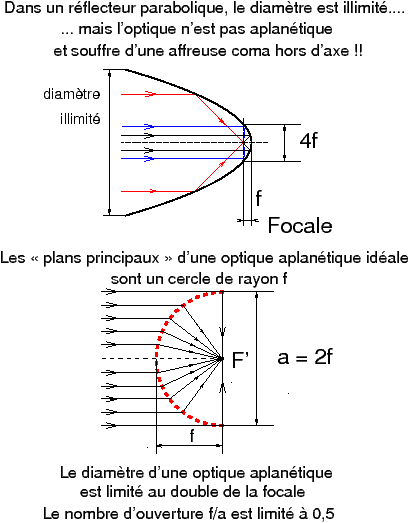
On a vu que le nombre d’ouverture « vrai » était toujours plus grand que 0,5, on peut se demander à quoi correspond une ouverture de 0,5. Le cas-limite est celui où les rayons arrivent presque parallèles au détecteur, une telle situation qui, si elle est techniquement impossible à réaliser avec des lentilles, est réalisable avec un miroir parabolique. Mais ce système, malheureusement pour les photographes, n’est pas capable de donner des images nettes dès qu’on s’écarte de l’axe (aberration de coma du miroir parabolique utilisé hors de l’axe de révolution de la parabole).
Figure 5 : Un miroir parabolique peut réaliser un nombre d’ouverture inférieur 0,5, mais pas une optique aplanétique
Outre une très fameuse série d’objectifs de chez Carl Zeiss ouvrant à 0,7 (popularisés au cinéma par le film Barry Lyndon de Stanley Kubrick en 1975), on fabriquait à l’époque des oscilloscopes cathodiques, des objectifs spéciaux à grande luminosité pour l’enregistrement de traces uniques sur film classique ou sur support à développement instantané. Les optiques ouvrant à f/1 sont très courantes de nos jours sur les intensificateurs d’images pour la vision nocturne, aujourd’hui devenus très accessibles à l’amateur pour l’aider dans ses manipulations photographiques en chambre noire.
On peut également signaler les lentilles de Fresnel utilisées dans les verres de visée et dans les concentrateurs solaires dont l’ouverture peut atteindre N = 0,7.
1.4 Origine des graduations des diaphragmes
La première question qui se pose est de savoir comment graduer les diaphragmes. On aurait envie de partir d’une graduation proportionnelle à la quantité de lumière reçue (figure 6). En fait, l’expérience montre que pour qu’une gamme de gris apparaisse à l’œil comme bien étagée, il faut que la progression des luminances des différentes plages soit en progression géométrique, c’est à dire que d’une plage à l’autre on multiplie la quantité de lumière émise par le même facteur. Ou encore, en utilisant la notion de densité optique [8], que la progression des densités soit régulière, on passe d’une plage à l’autre par une même marche ou échelon de densité (figure 7).
|
Figure 6 : Si on fabrique une gamme de gris dans laquelle la progression des luminances ou des éclairements est une progression arithmétique, c’est à dire qu’on passe d’une plage à la suivante en ajoutant ou retranchant un nombre constant de photons émis ou un nombre de lux constant, on obtient quelque chose qui n’est pas une bonne gradation sur le plan physiologique. Il y a trop de plages dans les hautes lumières. |
 |
|
Figure 7 : Une gamme de gris en progression géométrique sur les luminances ou les éclairements, c’est à dire qu’on passe d’une plage à la suivante en multipliant ou divisant le nombre de photons par un facteur constant, est perçue comme étant une bonne gradation sur le plan physiologique. On peut aussi dire qu’il s’agit d’une gamme de densités en progression arithmétique, on passe d’une plage à l’autre en ajoutant ou retranchant une valeur de densité constante. |
 |
Pour qu’une image sur film, sur support papier ou sur écran soit représentée de façon agréable en terme de gradation des niveaux de luminance, il convient de respecter cette progression géométrique des luminances. Il se trouve que pour le film, à condition de choisir un temps de pose correct, il est possible de transférer au moins une partie de la gamme des luminations (éclairements × temps de pose) à l’enregistrement, en une gamme de gris bien graduée sur le film (partie linéaire de la courbe caractéristique de noircissement dans le diagramme classique de Hurter et Driffield [9], voir figure 8).
|
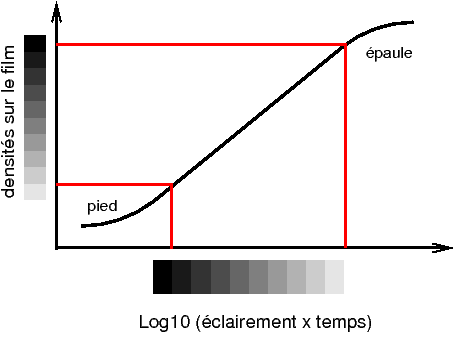
Figure 8 : La courbe caractéristique du noircissement d’un film relie les luminations (éclairements × temps de pose) en échelle logarithmique à la densité optique. Si possible il est préférable de régler la lumination pour que la gamme de luminances de la scène tienne dans la partie linéaire de la courbe. Ce n’est pas toujours possible lorsque la scène présente un très grand écart de luminances. Le pied de courbe et l’épaule sont propres au noircissement du film. Dans un détecteur photo-électrique silicium, il n’y a pas de pied, et l’équivalent de l’épaule est en fait une saturation assez brutale. Mais la conversion des nombres de photo-électrons reçus (un nombre proportionnel au nombre de photons reçus) en niveaux dans l’image finale, doit tenir compte, par un calcul, de la correction physiologique permettant en sortie une gamme de gris bien graduée. En d’autres termes, ce qui s’effectue de façon analogique dans le diagramme de noircissement du film est en fait recalculé dans un système d’imagerie photoélectrique numérique destiné à des images humainement lisibles. |
|
On a une situation un peu analogue en acoustique : pour qu’on ait une impression de progression régulière sur le volume du son, il faut commander la puissance électrique en progression géométrique par un potentiomètre dit « logarithmique ». Ou encore, pour ce qui est de la progression des fréquences musicales dans une gamme tempérée, on passe d’une note au demi-ton supérieur en multipliant sa fréquence par le même facteur égal à 1,059 ((2)1/12), d’un ton à un autre ton en multipliant par 1,122 ((2)1/6).
Cette nécessité de régler les quantités de lumière reçues (les luminations) en progression géométrique, explique les graduations des vitesses, où on passe d’un cran à l’autre par multiplication ou division du temps de pose par un même facteur. On a décidé un peu arbitrairement que un cran entier de diaphragme ou de vitesses correspondrait à un facteur deux sur les luminations, donc pour que la lumination soit divisée par deux il faut que la quantité Neff2 soit multipliée par 2 ; autrement dit Neff doit être multiplié par racine carrée de deux soit 1,414 ; ce qui revient à dire que pour doubler la lumination à temps de pose donné, le diamètre de l’iris doit être multiplié par √2, le nombre d’ouverture correspondant étant divisé par √2.
Le choix de ce facteur 2 comme base du « crantage » n’a rien de fondamental. On aurait pu choisir n’importe quel facteur pour cette progression des vitesses et des diaphragmes. En acoustique, le facteur 2 sur les fréquences dans une gamme musicale, l’octave, a une origine fondamentale liée aux différentes fréquences des modes d’oscillation d’une corde vibrante ; ce qui est connu, dit-on, depuis Pythagore lui-même. Mais pour ce qui est du volume sonore, comme pour le réglage de luminosité et des temps de pose en photographie, rien n’impose le facteur 2 comme unité du « crantage ».
On pourra se reporter à la notice Wikipédia en anglais pour plus d’informations concernant l’origine historique des graduations pour les nombres d’ouverture [10].
Les objectifs sont en général gradués pour la quantité N = N∞ et non pas Neff parce qu’on travaille en général en infini-foyer, ou du moins à des distances telles qu’il n’y a pas lieu de se préoccuper du facteur de soufflet (voir paragraphe 1.6) ; tant que les grandissements ne dépassent pas 0,2 = 1/5, la correction de facteur de soufflet est négligeable.
La série normalisée des diaphragmes est actuellement basée à partir de N=1 en progression géométrique de raison √2, c’est à dire qu’on obtient le cran de diaphragme immédiatement supérieur en multipliant N par 1,414 :
|
Table
1: |
|
En réalité au lieu de 5,6, il faudrait lire : 5,7 ; au lieu de 11, il faudrait lire : 11,3 et au lieu de 22 : lire 22,6 ; mais ces valeurs arrondies sont consacrées par l’usage.
Certains objectifs de chambre sont gradués en tiers de diaphragme, on peut se demander pourquoi. La raison probable en est la corrélation avec les échelles de sensibilité ISO des films qui progressent par subdivisions en tiers de diaphragme également, l’origine étant dans la définition des échelles logarithmiques DIN (voir annexe technique).
Si on intercale une série par demi diaphragmes entre les valeurs normalisées, on tombe sur la série suivante, valeurs arrondies au dixième le plus proche :
|
Table
2 : |
|
La même table par tiers de diaphragmes :
|
Table
3 : |
|
1.5 Ouverture géométrique ou photométrique ?
À ce stade de la discussion il est bon de rappeler une petite subtilité qui date de l’époque où les zooms de cinéma avaient déjà beaucoup de lentilles mais pas forcément des traitement anti-reflets aussi efficaces qu’aujourd’hui. Il y avait deux échelles distinctes, une échelle photométrique correspondant au produit T / (4N2) pour tenir compte de ce que le facteur T pouvait être notablement inférieur à l’unité, et une autre échelle géométrique correspondant au terme 1 / (4 N2) ; c’est à dire graduée uniquement en fonction du nombre d’ouverture ou du diamètre de l’iris, et qui détermine la profondeur de champ. Les opérateur calaient donc leur pose sur l’échelle photométrique, mais estimaient la profondeur de champ sur l’échelle géométrique.
La quantité
est appelée nombre d’ouverture photométrique de l’objectif, et représente le nombre d’ouverture qu’aurait un objectif parfait fournissant le même éclairement, si son facteur de transmission était de 100%.
Sur les objectifs de chambre modernes traités multi-couches dont le nombre de lentilles dépasse rarement 6 à 8 il n’y a pas lieu de se préoccuper de cette distinction, sur les zooms de petit et moyen format à grand nombre de lentilles, la prudence s’impose, mais dans les boîtiers automatiques dont les objectifs transmettent l’indication de diaphragme au calculateur de pose, il est parfaitement possible de tenir compte précisément du facteur T pour chaque objectif, et comme les échelles de profondeur de champ ont tendance à disparaître sur les appareils « modernes », la question n’est plus d’actualité. Mais il faut garder à l’esprit que le facteur T peut parfois, pour une optique ancienne, jouer des tours dans la détermination de la quantité effective de lumière qui atteint le film. Bien entendu si un filtre est placé devant l’objectif, le coefficient T va s’identifier avec l’inverse du coefficient prolongateur (multiplicateur) de temps de pose pour ce filtre.
Table de correspondance entre les coefficients prolongateurs de pose et les crans de diaphragme suivant les formules :
|
Table 4 : Coefficients prolongateurs de pose et crans de diaphragme, table en demi diaphragmes |
|
|
Table 5 : Coefficients prolongateurs de pose et crans de diaphragme, table en tiers de diaphragmes |
|
|
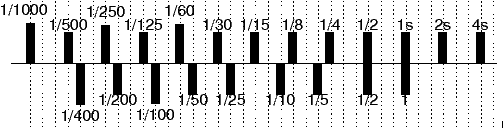
Figure 10 : Correspondance en tiers de diaphragmes pour les vitesses des anciens obturateurs |
1.6 Facteur de soufflet en macro, dans le modèle de la lentille mince
On appel facteur de soufflet (F.S.) le coefficient multiplicatif à appliquer au temps de pose pour garder la même lumination, afin de compenser la perte d’éclairement dans l’image due à l’augmentation du tirage total objectif-film d ; en d’autres termes, le fait que Neffest plus grand que N lorsque l’objet est à distance finie.
Ce coefficient F.S. est égal à
| F.S. = E(d)/ E(f) = Neff2 / N2 = (d/f)2 = (1 + (ext/f))2 (9) |
où ext est l’extension supplémentaire du tirage en macro par
rapport à la position infini-foyer,
d = f + ext.
Les lois de Descartes pour la lentille mince nous disent que l’extension de tirage ext est reliée au grandissement G par la formule :
| ext = G × f (10) |
ce qui donne une autre expression du facteur de soufflet dans le modèle de la lentille mince :
| F.S. = (1 + G)2 (11) |
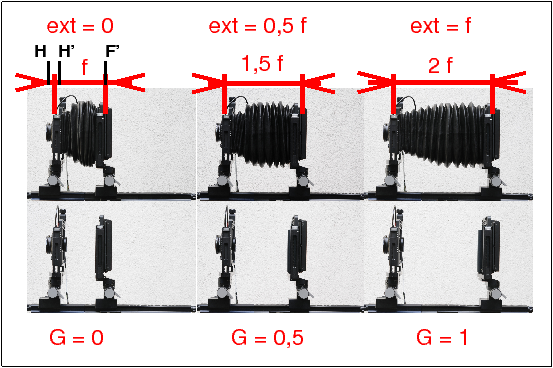
En particulier en position 2f-2f, on a : d=2f, ext = f, G=1 ; le facteur de soufflet F.S devient dans ces conditions égal à 22 = 4, soit + 2 crans de diaphragme.
2 Pupille d’entrée et pupille de sortie dans une optique épaisse
2.1 Définition des pupilles
Pour introduire la notion de pupilles, nul besoin d’aller chercher un système optique compliqué ni de s’équiper d’un logiciel de simulation. Il suffit par exemple de repartir d’une lentille simple diaphragmée (figure 12) et d’écarter progressivement vers l’avant le diaphragme de la lentille (figure 13).
|
|
|
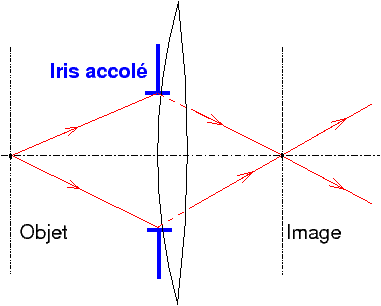
Figure 12 : Lentille simple avec diaphragme accolé : iris et pupilles sont confondus |
Dans la lentille simple avec diaphragme accolé, il n’y a pas lieu de distinguer l’iris des images qu’en donne la lentille, car les plans principaux d’une lentille mince étant confondus avec le plan de la lentille elle-même, qu’on regarde l’iris de quelque façon que ce soit, l’image qu’on en voit est identique à l’iris lui-même.
|
Figure 13 : |
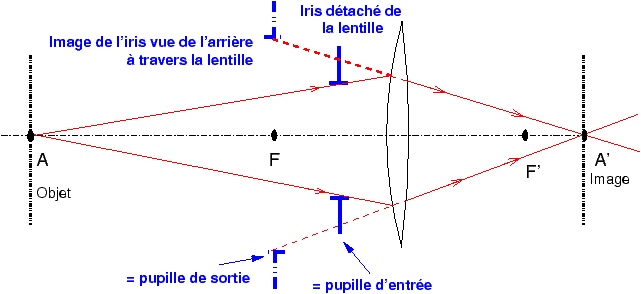 |
Écartons progressivement le diaphragme vers l’avant en le gardant bien centré sur l’axe, et supposons pour commencer que la monture de la lentille est assez grande. On peut montrer que dans ce système c’est bien entendu toujours le diaphragme qui va limiter les faisceaux utiles et la luminosité de l’objectif ainsi constitué. Mais la différence par rapport à la lentille simple avec iris accolé c’est que les deux images du diaphragme données par la lentille vers l’avant et vers l’arrière ne sont plus confondues.
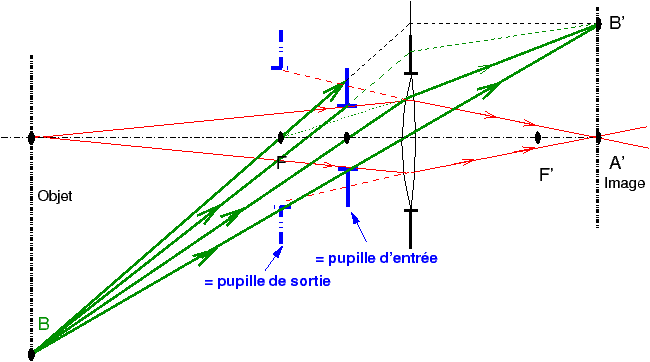
Par définition on appellera pour un système épais quelconque :
-
pupille d’entrée : l’image du diaphragme donnée vers l’avant par la partie avant du système optique,
-
pupille de sortie : l’image du diaphragme donnée vers l’arrière par la partie arrière du système optique.
Dans le cas particulier de la figure 13, la pupille d’entrée est confondue avec le diaphragme lui-même, la pupille de sortie est donnée par un tracé de rayons classique. Dans l’exemple de la figure 13, on a placé le diaphragme à une demi-distance focale en avant de la lentille ; vue de l’arrière, l’image du diaphragme est virtuelle et elle est située à une fois la distance focale en avant de la lentille (c’est bien entendu un cas particulier pour notre démonstration). On remarque également que la pupille de sortie a un diamètre différent de celui de la pupille d’entrée, dans le cas présent, deux fois plus grand.
La pupille d’entrée limite les rayons acceptables par le système, et les propriétés fondamentales des pupilles sont :
-
vue du film, la pupille de sortie est parmi les images de tout ce qui limite le diamètre des lentilles celle dont le diamètre est vu sous l’angle le plus petit ; sauf erreur dans la conception de l’objectif, c’est le diaphragme-iris réglable qui doit évidement jouer ce rôle ; tout rayon passant par la pupille d’entrée, et qui n’est pas intercepté par d’autres montures de lentilles dans l’objectif, repasse par la pupille de sortie et contribue à former l’image.
La figure suivante (figure 14) montre un tracé plus détaillé avec l’interception possible des rayons inclinés par la monture de la lentille. La lumière n’étant jamais totalement absorbée, elle peut être réfléchie et diffusée à l’intérieur de l’objectif et finir par sortir vers le film ou le détecteur, il y a là une source de lumière parasite diffuse qui affecte même les meilleurs objectifs.
|
Figure 14 : |
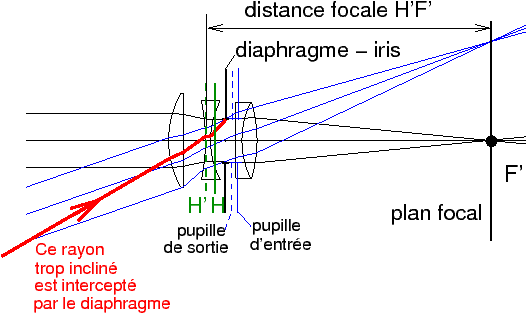
Ci-dessous (figure 15) on a pris un exemple plus intéressant pour le photographe, celui d’une formule Tessar à 4 lentilles en 3 groupes, des rayons trop inclinés qui ont réussi à entrer dans l’objectif sont finalement interceptés par le diaphragme (ou plus généralement par les montures des lentilles).
Dans un Tessar, les deux pupilles sont situées à l’intérieur de l’objectif, très près de l’iris lui-même, leur diamètre est très proche de celui de l’iris.
|
Figure 15 : Obstruction des rayons trop inclinés à l’intérieur d’un objectif, par exemple dans cette optique de type Tessar. On remarquera que sur ce Tessar particulier, les plans principaux H et H’ sont croisés, H’ est devant H. |
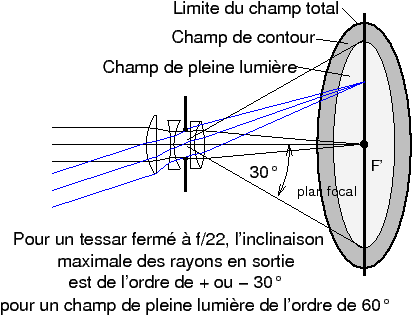
Dans tous les objectifs photographiques, il existe toujours une inclinaison maximale admissible pour les rayons, en entrée et donc en sortie, qui va définir le champ de vision utile de l’objectif côté objet et la surface effectivement éclairée dans l’image. C’est à dire du côté de l’objet l’ensemble des points de la scène capables de former une image sur le film ou le détecteur. À l’ensemble de ces points-objets correspond l’ensemble des points-images appelé champ total. On dit qu’un point de l’image est à l’intérieur du champ total s’il y a au moins un rayon qui relie l’objet à l’image en passant à travers tout l’objectif sans être intercepté par une monture ou par le diaphragme. Lorsque tous les rayons délimités par le diaphragme arrivent dans l’image, on dit qu’on est dans le champ de pleine lumière. Si le cône de rayons est délimité à la fois par le diaphragme et le bord d’une monture de lentille, la luminosité de l’image disparaît rapidement, on dit qu’on est dans le champ de contour (figure 16).
|
Figure 16 : Champ de pleine lumière, champ de contour et champ tota |
|
Figure 17 : |
 |
|
Figure 18 : |
 |
|
Figure 19 : |
 |
|
Figure 20 : |
 |
|
Figure 21 : |
 |
|
Figure 22 : |
 |
|
Figure 23 : |
 |
|
Figure 24 : Le Sonnar 5,6 de 250 mm Zeiss (ici en monture Hasselblad C) est un télé-objectif de grandissement pupillaire égal à 0,57. Son plan principal image H’ est dans l’air à 23 mm devant première lentille. Sur l’image en haut à gauche, on a fait la mise au point sur la pupille d’entrée, cette pupille se situe à 125,5 mm derrière la première lentille, soit environ à 20 mm devant la face avant de l’appareil. |
 |
Pour les anciens objectifs, la qualité d’image chutait rapidement avant qu’on n’ait atteint le champ de contour, mais avec les objectifs de chambre modernes on peut utiliser l’image pratiquement jusqu’au début du champ de contour avec une perte de qualité minime. Dans les photos du "Vieux Paris" d’Eugène Atget, on voit souvent en haut de l’image un cercle noir qui est la limite du champ total de l’objectif. Atget décentrait le plus possible pour garder les verticales des édifices parallèles dans l’image, mais il n’avait pas à sa disposition les optiques grand-angulaires modernes permettant une marge de décentrement considérable.
À l’intérieur du champ de pleine lumière, la luminosité de l’image n’est pas uniforme, l’analyse de ce phénomène fera l’objet d’un article séparé.
Dans un premier temps, on va négliger le fait que la qualité d’image diminue toujours en bord de champ, on ne prendra en compte que les tracés symboliques des rayons d’après les éléments cardinaux (plans principaux et foyer) sans tenir compte des aberrations.
On doit donc faire confiance aux ingénieurs pour avoir placé le diaphragme correctement, ce n’est pas une affaire simple, disons qu’en général dans les optiques de chambre quasi-symétriques, l’iris est placé au centre de symétrie du système, un endroit où très souvent dans les optiques photographiques les faisceaux sont de plus petit diamètre. Dans un objectif dissymétrique comme un télé-objectif, le placement du diaphragme ne peut donc plus obéir à cette règle simple d’être placé au « centre de symétrie » qui est l’emplacement privilégié du diaphragme [11] dans les systèmes quasi-symétriques ; en revanche il est avantageux pour minimiser le diamètre de l’obturateur de placer le diaphragme à l’endroit où le faisceau est le plus petit possible. Mais le placement du diaphragme dans une optique dissymétrique obéit à d’autres contraintes et compromis, en particulier concernant la réduction des aberrations et de la distorsion.
La pupille d’entrée étant l’image de l’iris vers l’avant, donnée par le demi-système antérieur, la pupille de sortie étant l’image de l’iris par le demi-système arrière, la pupille de sortie est donc l’image de la pupille d’entrée vue à travers la totalité du système.
Dans le cas général, il n’est pas possible de savoir où sont placées les pupilles sauf en lisant les documentations du constructeur ou en faisant une photographie de ces images du diaphragme avec un autre appareil photo équipé d’une graduation de distances.

Figure 25 :
Avec une
formule très dissymétrique comme le Télé-Arton de 360 mm
(focale réelle = 353 mm), on s’écarte résolument du
modèle de la lentille mince. Les plans principaux sont
très éloignés l’un de l’autre et très éloignés de la
planchette ; le plan principal objet H est situé dans
l’air à 137 mm devant la première lentille, le plan
principal image H’ est également situé dans l’air, en
avant de l’objectif, à 63 mm devant la première
lentille. Les pupilles ne sont plus situées aux plans
principaux, il s’en faut de beaucoup : ici la pupille
d’entrée est située un peu derrière la planchette, assez
profond à 130 mm derrière la première lentille, à 6 mm
derrière la lentille de sortie. La pupille de sortie est
située devant la pupille d’entrée, dans l’obturateur,
très près de l’iris, environ à 10 mm devant la
planchette. Pour ce télé-objectif, le grandissement
pupillaire est plus petit que l’unité, il vaut environ
0,57.
Dans le cas particulier de la figure 13, le tracé de rayons nous permet de montrer que la pupille de sortie se trouve vers l’avant, que son diamètre est plus grand que celui de la pupille d’entrée ; de façon générale ce sera le prolongement des rayons en sortie qui semblent provenir de la pupille de sortie.
|
Figure 26 : |
 |
Par définition, on appellera grandissement pupillaire Gp le rapport des diamètres des pupilles, sachant que ce grandissement est défini comme pour les images comparées à l’objet (voir figure 26) :
| Grandissement Pupillaire Gp = | ⎛ ⎝ |
diamètre de pupille de sortie | ⎞ ⎠ |
/ | ⎛ ⎝ |
diam. de pupille d’entrée | ⎞ ⎠ |
(12) |
Par exemple sur les figures (13) et (14), l’emplacement particulier du diaphragme à une demi-distance focale en avant de la lentille conduit à un grandissement pupillaire égal à 2. Pour le Tessar de la figure (15) le grandissement pupillaire est très voisin de l’unité, il vaut 0,91.
2.2 Lien entre grandissement pupillaire et position des pupilles
Les pupilles sont images l’une de l’autre à travers le système. Donc leurs positions obéissent aux formules de conjugaison, leurs dimensions sont liées à leurs positions comme pour n’importe quelle image. Ces formules sont données dans l’annexe technique, mais on peut ici mentionner les résultats intéressants.
-
si le grandissement pupillaire est égal à un, les pupilles sont placées dans les plans principaux ;
-
pour un grandissement pupillaire supérieur à 1, la pupille de sortie est située en avant du plan principal image ; c’est le cas des grand-angulaires de formule « rétrofocus » ;
-
pour un grandissement pupillaire inférieur à 1, la pupille de sortie est située en arrière du plan principal image ; c’est le cas de certaines longues focales de formule « télé-objectif ».
Par exemple dans le Tessar de la figure 15, le grandissement pupillaire est de 0,91 ; les pupilles sont placées très près des plans principaux H et H’. On remarque que dans ce Tessar les plans principaux sont croisés (H’ est devant H), les deux pupilles tombent très près l’une de l’autre, et elles sont croisées également.
Un autre résultat très remarquable est le suivant : si un objectif est parfaitement symétrique avec l’iris placé au centre de symétrie, le grandissement pupillaire est égal à un et les pupilles qui sont les images de l’iris vers l’avant et l’arrière sont placées dans les plans principaux.
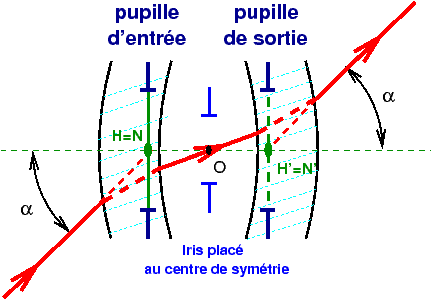
La démonstration de cette propriété se fait sans calcul grâce à un tracé de rayons très simple (figure 27).
|
Figure 27 : Une formule symétrique avec diaphragme centré a un grandissement pupillaire égal à l’unité |
On trace un rayon passant par le centre O du diaphragme qui est dans ce cas le centre de symétrie du système. Vers l’avant et vers l’arrière après réfraction, les deux rayons ont évidemment une inclinaison α différente de celle du rayon central, mais la symétrie impose que ces angles soient identiques en entrée et en sortie. En prolongeant ces rayons jusqu’à ce qu’ils coupent l’axe optique aux points N et N′, on obtient par définition les points nodaux de l’objectif puisque les angles d’inclinaison hors de l’optique, côté objet ou côté image, sont identiques. Dans notre cas avec l’iris placé au centre de symétrie ces points N et N′ sont également l’endroit où l’image du centre du diaphragme se forme. Si le système est dans l’air, points nodaux N et N′ et points principaux H et H′ sont confondus, d’après une propriété très générale des systèmes centrés indépendante du degré de symétrie du système. On en déduit d’après la propriété des plans principaux, pour lesquels le grandissement image/objet est égal à l’unité, que les deux pupilles sont de même diamètre et qu’elles sont situées dans les plans principaux, les centres des pupilles coïncident avec les points nodaux.
Tous les objectifs de chambre de formule quasi-symétrique ont un grandissement pupillaire très voisin de 1 et donc leurs pupilles sont situées très près des plans principaux. De même, le Tessar, bien de que de formule dissymétrique, a un grandissement pupillaire proche de l’unité. Pour tous ces objectifs, tout ce qu’on sait de la lentille mince à diaphragme accolé (figure 12) est applicable pratiquement sans restriction. Seul l’écart entre plans principaux modifie un tout petit peu les tracés de rayons, mais le comportement du système lorsqu’on le diaphragme, tout ce qui se passe en avant du plan principal objet et en arrière du plan principal image, que ce soit pour le facteur de soufflet ou la profondeur de champ, est exactement identique à celui de la lentille mince. Par exemple pour le Tessar de la figure 15, l’écart entre plans principaux n’est que de 2% de la distance focale du système, l’épaisseur totale entre le sommet de la première lentille et le sommet de la dernière lentille étant égal à 31% de la focale.
Seuls les objectifs dissymétriques à grandissement pupillaire notablement différent de l’unité, par exemple les rétrofocus, les télé-objectifs (ou les zooms en général) seront représentés par des formules photométriques plus complexes où entre en jeu le grandissement pupillaire.
2.3 Formules photométriques et nombre d’ouverture dans le cas général
Dans le cas général d’un système épais défini par son grandissement pupillaire Gp on a les propriétés suivantes :
-
la formule fondamentale de la photométrie (équation 3) reste valable à condition que l’angle α′ soit mesuré de l’axe jusqu’au bord de la pupille de sortie, figure 28 ;
-
la définition du nombre d’ouverture N = N∞ reste inchangée à condition de prendre en compte le diamètre a de la pupille d’entrée, sous la forme :
N = N∞ = f / a, f étant la focale.
le nombre d’ouverture N
est défini par référence
au diamètre de pupille d’entrée à
N = f / a (13)
N = N∞
qui est gravé sur les bagues des objectifs
|
Figure 28 : |
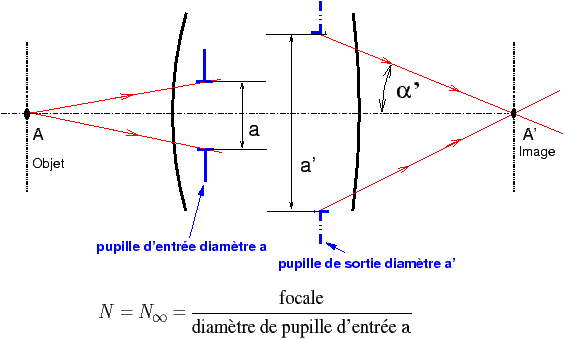 |
Les formules générales pour le facteur de soufflet dans une optique dissymétrique sont les suivantes :
| F.S. = (G+Gp)2 / Gp2 = | ⎛ ⎝ |
1 + G / Gp | ⎞ ⎠ |
2 (14) |
où G est le grandissement (image/objet) en valeur absolue et Gp est le grandissement pupillaire.
Ce grandissement pupillaire est une donnée fixe pour un objectif de focale fixe à groupes optiques fixes, donc il suffit de le connaître d’après les documentations du constructeur ou de le mesurer. Mais pour un zoom, il peut changer lorsque la focale change, car les pupilles et les plans principaux se déplacent à cause du déplacement des groupes de lentilles mobiles. Par exemple, un zoom « trans-standard » se comportera comme un rétrofocus de grandissement pupillaire plus grand que l’unité en position grand-angle, et comme un télé-objectif de grandissement pupillaire plus petit que l’unité en longue focale.
En position 2f-2f, comme d’habitude on a G = 1, ceci reste valable quelle que soit la formule optique. Et si Gp = 1 comme dans une lentille mince diaphragmée en son centre ou comme dans une optique symétrique, la formule générale (14) redonne la formule classique F.S. = (G+1)2.
Cette formule générale résulte de la loi des sinus d’Abbe et des formules de conjugaison pour les pupilles, elle est démontrée dans l’annnexe technique et est identique à celle de l’ouvrage de référence de L. Lefkowitz [13].
Figure 29 : Focalisation du Télé-Arton, de 360 mm (353 mm) de focale en infini-foyer, puis au grandissement G=0,25. En position infini-foyer, le tirage optique est de 210 mm environ, ce qui permet d’utiliser cette longue focale sur une chambre qui ne dispose pas d’un grand tirage.C’est tout l’intérêt d’une formule télé-objectif. Dès qu’on cherche à focaliser sur des objets proches, la formule du grandissement ext=G f s’applique de la même façon qu’avec une formule quasi-symétrique, les allonges de soufflet deviennent à nouveau importantes, l’extension au-delà du foyer étant en proportion directe de la focale, et il n’y a plus alors grand gain à utiliser un télé-objectif, le seul gain est sur le tirage de départ, le tirage mécanique en infini-foyer.
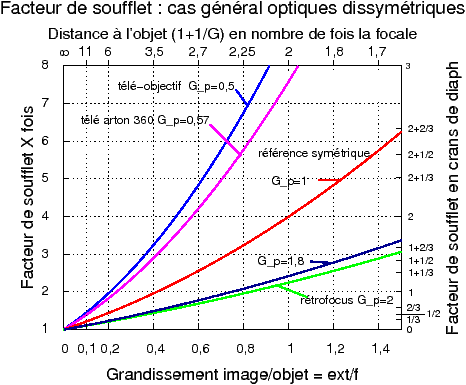
Le diagramme suivant (figure 30) permet de comparer la correction d’exposition ou facteur de soufflet à apporter en fonction du grandissement pour différentes optiques, les télés, les symétriques et les rétro-focus. Aux très petits grandissements, en-dessous de 0,1 soit pour un objet situé à 11 fois la focale en avant de l’objectif, donc pour les objets à grande distance, ces corrections sont faibles dans les trois cas. Mais dès que l’objet se rapproche, les courbes sont franchement distinctes. Par exemple pour le Schneider Télé-Arton de 360 mm dont le grandissement pupillaire est de 0,57 environ, au rapport G=0,5 (l’objet étant situé environ à 3 fois la distance focale, soit un peu plus d’un mètre pour un 360 de focale) l’écart de correction par rapport à l’optique symétrique est presque de 1/2 diaphragme, ce n’est pas négligeable. La correction totale étant de 1 diaph 2/3. Pour un rétro-focus de grandissement pupillaire égal à 1,8 (cas du Distagon Zeiss f/4 de 50 mm, voir plus bas) on constate que les corrections du facteur de soufflet sont inférieures à un demi-diaphragme environ en-dessous du grandissement 0,5.
|
Figure 30 : Facteurs de soufflet pour les optiques épaisses dissymétriques |
2.4 Nombre d’ouverture et facteur de soufflet pour une optique montée à l’envers
La fait que le nombre d’ouverture soit défini par le diamètre de la pupille d’entrée a une conséquence curieuse, c’est que l’objectif, s’il est de grandissement pupillaire différent de l’unité, peut voir son nombre d’ouverture changer lorsqu’on l’utilise à l’envers.
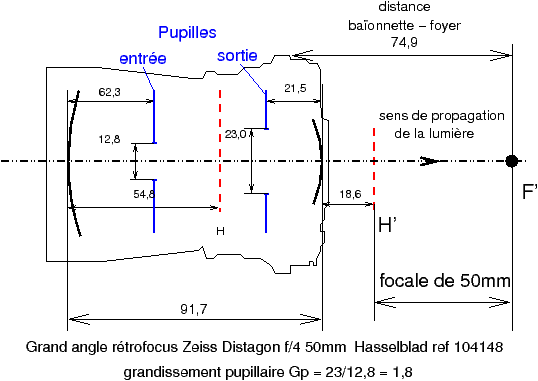
Pour cela, partons d’un objectif dissymétrique comme un grand-angulaire rétrofocus pour appareil reflex ; pour préciser les idées nous partirons d’un exemple réel, le Distagon Zeiss f/4 de 50 mm à groupes fixes.
|
Figure 31 : |
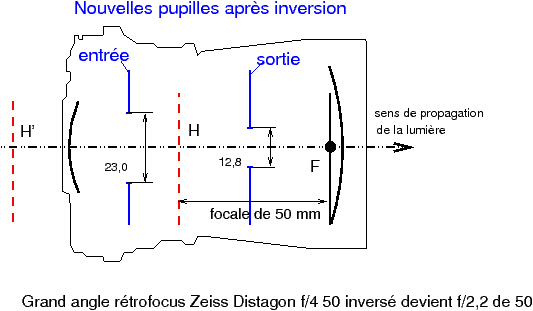
Lorsqu’on monte cet objectif à l’envers, le nombre d’ouverture devient 2,2. Mais l’optique une fois inversée devient inutilisable pour de la photo à grande distance, car son foyer objet, qui devient foyer image une fois inversé, tombe dans les verres ! De plus, même si on pouvait accéder à l’image, la qualité ne serait pas au rendez-vous, l’objectif n’ayant évidemment pas été conçu pour être utilisé à l’envers. Néanmoins on pourrait en principe utiliser ce Distagon à l’envers pour faire de la macro-photo, l’image se formant alors au-delà du foyer avec un grandissement notablement supérieur à l’unité.
|
Figure 32 : |
Monter une optique à l’envers est une solution permettant d’atteindre les grandissements supérieurs à l’unité à partir d’une optique dissymétrique courante prévue pour travailler avec des sujets lointains. Si l’optique est parfaitement symétrique comme un apochromatique classique de banc de reproduction, nul besoin d’inverser cet objectif à cause de la symétrie.
Le facteur de soufflet pour une optique dissymétrique inversée est donné par la formule suivante, qui donne la correction totale à appliquer sur la base d’une mesure faite avec un posemètre indépendant, en lisant les graduations de diaphragme sur l’objectif (lesquelles ne correspondent plus au véritable nombre d’ouverture inversé) :
| F.S.total / optique inversée = (G + 1/Gp)2 (15) |
où G est le grandissement (image/objet) dans les conditions de travail, par exemple 4x pour une image 4 fois plus grande que l’objet et Gp le grandissement pupillaire d’origine, celui de l’objectif donné par le constructeur lorsqu’il est non inversé (par exemple : Gp=1,8 pour le Distagon Zeiss de la figure 31).
Conclusion
Au terme de cet article nous avons mis en place la notion de pupille dans un objectif photographique. Au contraire des plans principaux qui sont une entité géométrique difficile à appréhender, les pupilles sont, en fait, ce que nous voyons du diaphragme d’un objectif dans l’usage courant. Certes on ne peut pas toucher ces pupilles, mais on peut les mesurer, par exemple en en prenant une photo. On peut déterminer leurs positions également par une visée optique ou par le calcul mais il faut alors connaître l’ensemble des caractéristiques des lentilles composant le système, ces données sont décrites dans les brevets. La plupart des fournisseurs d’objectifs à usage professionnel publient dans leurs fiches techniques les données concernant les dimensions et positions des pupilles.
La plupart des optiques de chambre y compris les grand-angulaires à l’exception des télé-objectifs (les rétro-focus sont quasi inexistants parmi les objectifs grand format [14]) sont des formules quasi-symétriques pour lesquelles le modèle de la lentille mince s’applique assez bien. Le modèle s’applique également assez bien aux formules faiblement dissymétriques comme les Tessars.
La conséquence est que les formules classiques du facteur de soufflet valables pour les optiques symétriques décrivent correctement presque toute la réalité des optiques utilisées en grand format en photo rapprochée, l’exception étant là encore les télé-objectifs. Mais avec un télé-objectif, pour que la formule simplifiée tombe en défaut, il faudrait travailler en proxiphoto, ce qu’on ne fait en général jamais avec ce genre d’objectif.
Remerciements
Cet article n’existerait pas sans de nombreuses discussions avec Yves Colombe. Le point de départ fut la question du meilleur point de rotation pour un appareil photo ordinaire lorsqu’on cherche à faire du raccordement panoramique d’images, ce meilleur point étant la pupille d’entrée de l’objectif. Clarifier cette question dont les explications sont probablement enfouies dans de vieux livres d’optique instrumentale oblige donc à revoir ce que sont les pupilles d’un système optique. Il est étonnant que des notions, a priori utiles aux seuls ingénieurs en optique, aient pu « descendre » jusqu’au grand public... merci Internet ! La discussion de départ avec Yves Colombe se trouve dans les archives [15] du forum http://galerie-photo.info.
L’analyse de ce problème de raccordement panoramique et le rôle joué par la pupille d’entrée dans le rendu de perspective fera l’objet d’un autre article.
Notes et Références
| [1] |
« Un objectif photographique n’est
pas une lentille mince ! » Première partie, introduction aux systèmes
optiques centrés épais, par Emmanuel Bigler et Yves Colombe
|
|
Moussa/Ponsonnet, « Optique géométrique » Cours de physique, tome 1. Optique , Casteilla (2000) ISBN : 2713512239
|
|
| [3] |
http://comprendre.meteofrance.com/jsp/site/Portal.jsp?
|
| [4] |
http://audience.cerma.archi.fr/cerma/pageweb/theorie/solaire/rayont_solaire.html
|
| [5] |
http://comprendre.meteofrance.com/pedagogique/pour_tous/glossaire/f/f_detail?
|
| [6] |
Base de radiometrie optique
|
| [7] |
Cours de J.L. Meyzonnette, Orsay
|
| [8] |
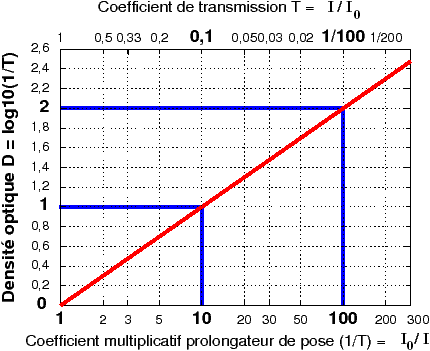
Par définition, on appelle densité optique D le logarithme décimal du rapport entre la quantité de lumière I0 qui éclaire une plage grise et la quantité de lumière réfléchie ou transmiseI par cette plage, D = log10(I0/I). Une densité optique de 0 réfléchit ou transmet 100% de la lumière, une densité de 1 réfléchit ou transmet 0,1 soit 10%. La propriété de base des logarithmes implique que lorsque la lumière réfléchie ou transmise est multipliée par une même quantité (échelle en progression géométrique), son logarithme et donc la densité augmente ou diminue d’une même quantité, d’un même « échelon de densité ».
|
|
|
|
|
Figure 33 :
|
|
| [9] |
La première étude quantitative du noircissement d’un film gélatino-bromure est due à Ferdinand Hurter (1844-1898) et Vero Charles Driffield (1848-1915). C’est toujours cette représentation reliant le log10 des luminations à la densité optique qui prévaut aujourd’hui dans la sensitométrie des films. http://en.wikipedia.org/wiki/Hurter_and_Driffield
|
| [10] |
F-number, article de Wikipédia
|
| [11] |
Dans une optique symétrique, le placement du diaphragme au centre de symétrie joue un rôle fondamental en minimisant la distorsion. Dans le cas très particulier où objet et image sont situés à la même distance, au rapport 1:1, une optique symétrique diaphragmée au centre de symétrie présente une distorsion nulle. De plus cette configuration où tout est symétrique annule la coma et le chromatisme transversal. Ces règles de conception tirant partie de la symétrie on été appliquées par les ingénieurs dès le XIXe siècle et servent encore de base de départ pour de nombreuses optiques de chambre. Sur ces aspects historiques on lira avec profit l’ouvrage de Rudolph Kingslake : A History of the Photographic Lens, Academic Press (1989), ISBN 0124086403
|
| [12] |
Sur les objectif Zeiss ouvrant à 0,7
utilisés dans le film Barry Lyndon on lira ce document, entre
autres :
|
| [13] |
La formule générale du facteur de soufflet pour une optique dissymétrique est donnée dans l’ouvrage de référence suivant : Lefkowitz, Lester. 1979. The Manual of Close-Up Photography. Amphoto. Garden City, NY. 272 pp. ISBN 0-8174-2456-3 (relié) ou 0-8174-2130-0 (broché). L. Lefkowitz ne donne pas la formule pour les optiques inversées, mais on la trouve dans l’excellent livre de René Bouillot La Pratique du Moyen Format, éditions VM, ISBN 2-86258-129-11, (Paris, 1993) page 55 ; et édition 1999 page 63. Noter que dans l’application numérique que donne R. Bouillot, le grandissement pupillaire a la valeur numérique inverse de celle qui devrait être mise dans les formules, par ailleurs exactes et qui correspondent bien à la définition Gp = (diamètre pupille de sortie) / (diamètre pupille d’entrée) qui est aussi celle de Lefkowitz. Donc dans le livre de René Bouillot, les formules sont les bonnes mais les valeurs numériques des grandissements pupillaires sont inversées ; ainsi, fort logiquement, les conclusions pratiques sont inversées par rapport à la réalité.
|
| [14] |
Jusqu’aux années 1990 il n’y avait aucune optique de conception rétrofocus (avec grandissement pupillaire supérieur à 1) pour les chambres grand format, tous les grands angulaires de chambre étant de conception quasi symétrique. Le développement des optiques de chambre pour prise de vue sur capteurs silicium de petit et moyen format relance l’intérêt d’une certaine dose d’effet rétrofocus dans les ultra-grand-angulaires, le but étant d’augmenter le tirage optique (distance libre entre la dernière lentille et le capteur) et d’améliorer l’homogénéité d’éclairement sur le champ, une question qui sera abordée dans un autre article. Par ailleurs la demande des professionnels pour des grands angulaires à bascule et décentrement en petit format pour prise de vue numérique a relancé récemment la conception de nouvelles optiques rétrofocus de haute performance pour appareil reflex.
|
| [15] |
Discussion avec Yves Colombe sur le raccordement panoramique et la pupille d’entrée (avril 2002) :http://www.galerie-photo.org/a-f-498.htmlCe très court message fut à l’origine de très nombreuses discussions, en particulier sur le rôle de la pupille d’entrée dans le problème du raccordement panoramique d’images sans effet de parallaxe. |
Version du 28 octobre 2011
Télécharger cet
article au format pdf
Télécharger l'annexe technique
de cet article au format pdf
Dernière modification de cet article : 2011
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||