[abonnement gratuit]

l'auteur

Télécharger la présentation au format pdf
Télécharger la présentation en anglais au format pdf (transparents uniquement)
 

Cette page fait partie des
Actes du IVème Congrès
de la photographie haute résolution
(Bourges 2008) :
interview de gérard métrot par jean demaison
l'objet photographique
le collectif dans l'édition photographique
le flare (1) - présentation expérimentale
le flare (2) - explication : lumière diffuse et réflexion parasite
le réel en photographie
photographe(s) - l'histoire d'un groupe
évolution du droit à l'image

Lumière diffuse et réflexions parasites

par Emmanuel Bigler

Résumé

Lumière diffusée, voile atmosphérique, lumière diffractée, lumière parasite, réflexions parasites, sont des phénomènes optiques bien connus des photographes et souvent considérés comme nuisibles à la qualité des images.
Cette présentation faite au congrès galerie-photo de Bourges en octobre 2008 est une introduction à ces questions.

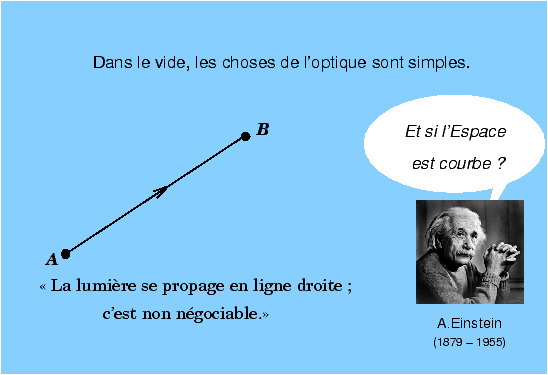
Figure 1
 

Dans le vide, l’optique serait simple

Se rappelant l’histoire de la Colombe d’Emmanuel Kant [1], le photographe confronté aux effets nuisibles du voile atmosphérique dans le paysage et autres phénomènes de lumière parasite diffuse pourrait être tenté, comme dans certaines introductions à l’optique faites au tableau noir, de ne considérer que la propagation de la lumière dans le vide (figure 2). Certes, dans le vide, rien en principe ne vient perturber la propagation de la lumière qui se propage, du moins à notre échelle humaine, en ligne droite. Sachant que sur la Lune le vide est plus poussé que dans aucun appareillage existant sur Terre, la tentation serait donc grande d’aller sur la Lune rien que pour faire des photos en étant enfin débarrassé de la lumière diffuse.

Figure 2

Hélas ! (figure 3) dès qu’on arrive sur la Lune, les ennuis commencent. Certes l’absence d’atmosphère garantit un ciel bien noir et une vue imprenable sur le clair-de-Terre, mais le nécessaire filtre antiradiations du casque de l’astronaute nous apporte son lot de réflexions parasites, et le sol lunaire, granuleux et pulvérulent à souhait, est un magnifique diffuseur gris, nettement plus gris, soit dit en passant, que les fameux cartons gris à 18% de réflexion [2].

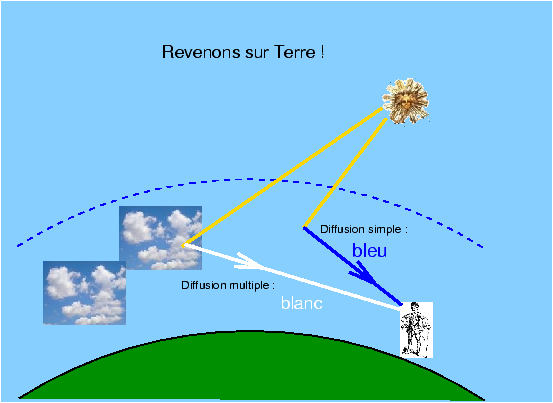
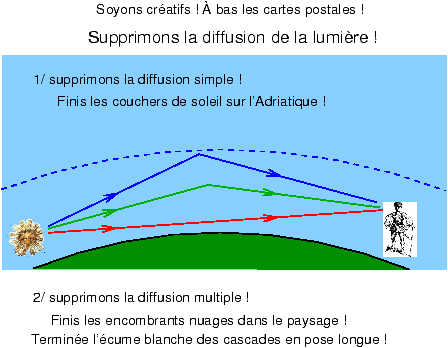
Figure 3

Revenons sur Terre...

Revenant sur Terre, force nous est de constater que la lumière diffusée est une donnée première du paysage. La diffusion de la lumière solaire par les molécules de l’air nous renvoie une teinte bleue bien connue et si appréciée que les photographes du XIXème siècle, fâchés de ne pouvoir enregistrer, à défaut de la couleur, que des ciels vides (ceci à cause de la sensibilité de leurs plaques à cette seule lumière bleue) étaient déjà obligés de recourir au photomontage pour faire apparaître des nuages blancs dans leurs tirages.

Le fait que les nuages soient blancs signe la présence d’un phénomène de diffusion multiple des rayons lumineux sur les fines gouttelettes en suspension, au contraire du bleu du ciel qui est une diffusion simple [3] par des particules dont les dimensions inférieures au nanomètre sont très inférieures à la longueur d’onde de la lumière visible (0,4 à 0,8 µm).

Dans la diffusion simple, les courtes longueurs d’onde (UV, bleu) sont plus efficacement diffusées que les longues (orange, rouge), donc de jour puisqu’on ne peut pas regarder au voisinage du soleil, c’est le bleu qui domine la couleur du ciel, provenant des rayons diffusées sous un angle qui peut facilement dépasser 90° et atteindre 180°, en un demi-tour complet.

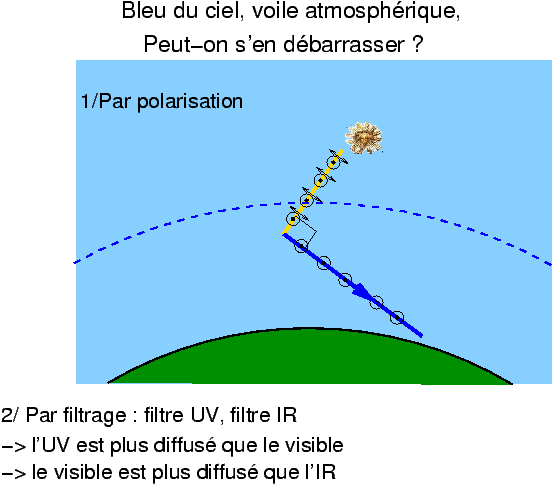
Figure 4

Au soleil couchant, l’épaisseur d’air traversée augmente, joue partiellement le rôle d’un filtre absorbant, et permet d’observer un dégradé de couleurs juste autour du soleil, dans l’ordre des couleurs de l’arc en ciel, le rouge étant le plus proche du soleil. On observe également un dégradé similaire dans le ciel à l’opposé du soleil couchant.

Dès qu’il y a diffusion multiple, cet effet sélectif sur les couleurs disparaît au profit d’un mélange redonnant du blanc, c’est le cas des nuages ou du brouillard.

En photo de paysage, cette lumière diffusée se rajoute à la lumière réémise directement par les objets lointains. Il y a donc une perte de contraste et de visibilité des objets lointains. La diffusion et l’absorption peuvent être plus importantes si l’air est chargé de poussières ou de vapeur d’eau ; d’une façon générale l’effet de voile atmosphérique ne disparaît que dans les régions désertiques, en conditions froides. En effet, les mouvements de l’air sous l’effet des différences de température sont un autre facteur de dégradation importante de la qualité des images.

Pour redonner du contraste aux nuages sur fond de ciel, outre les classiques filtres jaunes/oranges/ rouges de la photo en noir et blanc, il est possible de couper la lumière diffusée à l’aide d’un filtre polarisant (figure 5).

Figure 5

Par suite de la transversalité des champs électromagnétiques qui forment la lumière, on peut montrer que ces rayons diffusés à 90° sont polarisés rectilignement, la vibration réémise par diffusion ne pouvant pas être alignée suivant la direction de propagation du rayon renvoyé vers l’observateur [4]. De ce fait la lumière du ciel diffusée à 90° de la position du soleil, vue de l’observateur au sol, peut être coupée par un verre polarisant d’orientation croisée par rapport à la direction de la polarisation incidente. Cet effet de polarisation à la prise de vue n’empêche pas l’enregistrement de la lumière non polarisée émise par le sujet –moyennant une augmentation de pose– ou celle issue des diffusions multiples (comme les nuages) ; d’où l’amélioration du contraste des nuages sur fond de ciel, ou des blanches montagnes lointaines sur fond de ciel volontairement assombri. Le verre polarisant est donc également très utilisé en photo couleurs de paysage, car c’est un autre moyen d’assombrir le ciel sans toucher aux nuages tout en respectant les couleurs du paysage (ce que ne font pas, bien entendu, les filtres jaunes/oranges/rouges).

Soyons créatifs, supprimons la lumière diffusée !

Les couchers de soleil et les nuages sur fond de ciel bleu font partie de ces images rebattues des cartes postales, images dénoncées comme des poncifs photographiques par les artistes créatifs, finalement en supprimant toute lumière diffuse dans le paysage, les choses seraient effectivement plus simples (figure 6).

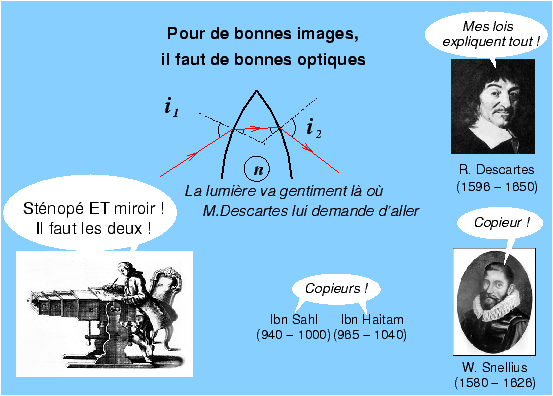
Figure 6

Et dans l’appareil, çà diffuse aussi ?

À ce point de l’exposé, les lecteurs peuvent s’impatienter légitimement, car ce qui les intéresse, c’est plus ce qui se passe dans leur appareil et dans leurs objectifs, du moins lorsque l’image se forme à travers un empilement de verres d’optique plutôt qu’un sténopé.

Dans le principe, tout ce qui concerne la formation des images à travers un objectif découle des lois de la réflexion et de la réfraction (figure 7).

En France, il est d’usage de créditer René Descartes pour les lois de la réfraction, mais dès qu’on sort de France, on ne connaît plus que les lois de Snell ou de Snellius, lesquelles lois étaient déjà connues des mathématiciens Arabes du Moyen-âge [5]. Toujours est-il que la lumière est censée se propager là où on l'attend lors de la traversée des différents dioptres, entre ces dioptres elle se propage en ligne droite sauf exceptions rares [6], les lois de la réfraction ne laissent en rien présager de quelque effet de lumière parasite diffuse !

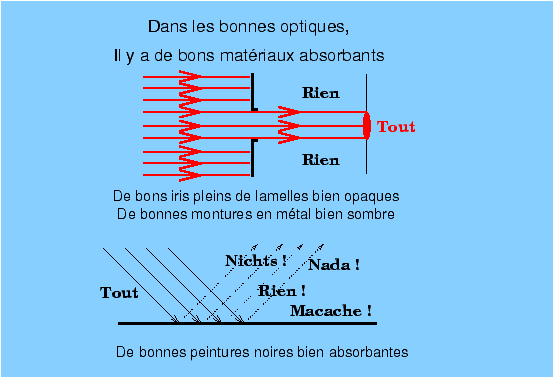
Figure 7

Dans un monde optique idéal bien que devenu très matériel depuis qu’on a renoncé au vide comme seul milieu de propagation, les matériaux seraient soient transparents soit absorbants, les trajets des rayons seraient simples et sans échappatoire possible ; les diaphragmes ou montures métalliques seraient parfaitement absorbants et les surfaces peintes en noir ne réfléchiraient rien du tout (figure 8).

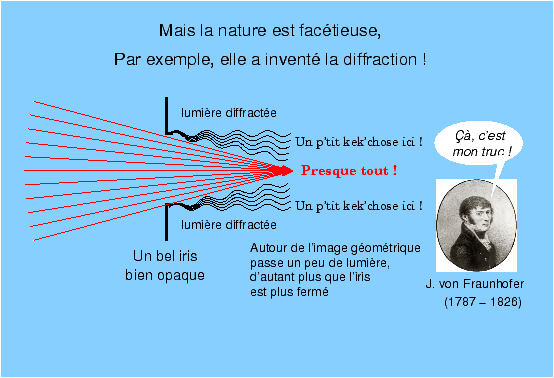
Figure 8

Or, il y a toujours un peu de diffraction...

Or si on regarde d’un peu plus près ce qui se passe lorsque la lumière traverse un objectif, même si les matériaux composant le diaphragme et les montures sont parfaitement absorbants et non réfléchissants, même si l’objectif est parfaitement corrigé de toutes les aberrations géométriques, la lumière refuse de se concentrer en un seul point, car par suite de la diffraction (figure 9), il y a toujours un peu de lumière qui s’écarte du chemin prédit par les lois de la propagation rectiligne [6], de la réflexion et de la réfraction.

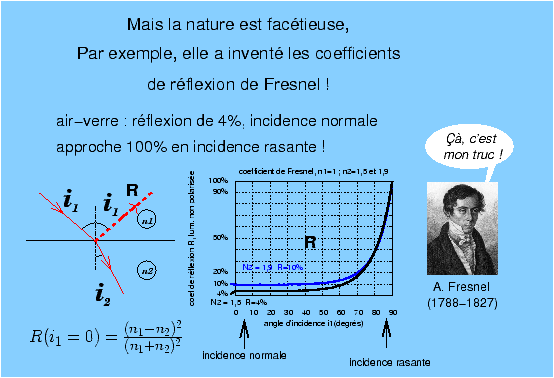
Figure 9

M. Augustin Fresnel nous réserve une autre surprise !

Il faudra donc accepter que la diffraction impose une limite fondamentale à la qualité des images, mais avant cela, il faut tenir compte d’un autre phénomène probablement connu des physiciens avant le XIXème siècle, mais qui fut formalisé par Fresnel (1788-1827), c’est à dire la réflexion parasite d’une partie de la lumière à la traversée de chaque dioptre (figure 10).

Le fait que la lumière puisse se réfléchir sur autre chose qu’un miroir poli métallisé est une expérience courante, il suffit de penser aux reflets du soleil sur l’eau. Chaque fois que la lumière tombe sur un dioptre, une partie est réfléchie comme sur un miroir. La figure 10 montre la variation du coefficient de réflexion, appelé coefficient de Fresnel, sur une interface air-verre en fonction de l’angle d’incidence, pour un verre classique d’indice n=1,5. En incidence normale, environ 4% de la lumière est réfléchie, soit une transmission de 96%. Lorsque l’angle d’incidence augmente, ce coefficient reste assez proche des 4% jusqu’à 45° environ, mais ensuite lorsque les rayons deviennent rasants, le coefficient augmente très vite jusqu’à atteindre 100%.

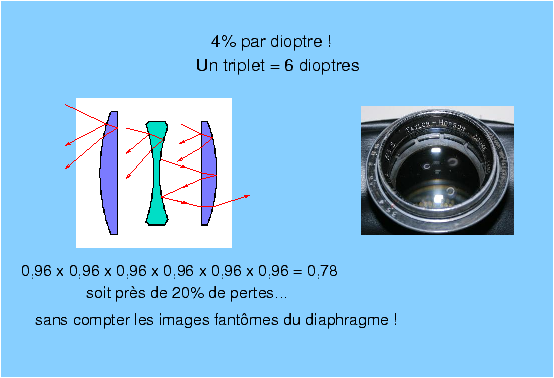
Figure 10 : Coefficients de réflexion de Fresnel

Plus de lentilles = meilleures images ?

Pour améliorer la performance des optiques (ce qui est également vrai pour les verres ophtalmiques), il est également utile d’utiliser des verres d’indice élevé, ce qui permet de réduire la courbure des verres pour une puissance donnée et donc de réduire certaines aberrations. Avec un verre d’indice 1,9, le coefficient de réflexion en incidence normale monte à 10%, sans traitement antireflet, là encore ces verres seraient très difficilement utilisables en pratique.

Cette perte par réflexion s’effectue sur chaque dioptre, dans une lentille mince il y a deux dioptres et si on considère un objectif simple et classique comme le triplet de Dennis Taylor [7] (figure 11), la lumière effectivement transmise par l’objectif tombe à 78% de ce qui rentre. S’il n’y avait qu’une perte par absorption, ceci se traduirait par une perte de luminosité de l’ordre du demi-diaphragme, il suffirait d’en tenir compte dans la graduation des bagues de diaphragme [8]. Le problème est plutôt que les rayons parasites réfléchis sur les dioptres ne sont pas forcément tous absorbés par les montures, il peuvent après plusieurs aller-retour se superposer à l’image principale soit sous forme d’images-fantômes de l’iris, soit en ajoutant un fond de lumière diffuse sans forme reconnaissable.

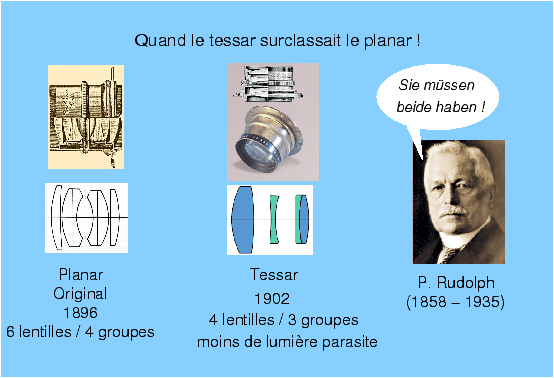
Figure 11 : Le triplet de Dennis Taylor, non traité,
ne transmet que 78% de la lumière

Quand le Tessar surclassait le Planar !

Depuis le premier doublet de lunette astronomique [9] conçu au XVIIIème siècle, on sait que pour améliorer les performances des objectifs, il faut combiner différentes lentilles de formes et de types de verres différents. Dès la fin du XIXème siècle, les ingénieurs proposent des combinaisons de plus en plus compliquées, et pour limiter les réflexions parasites, ils ont recours à des doublets et même des triplets collés [10]. La perte par réflexion augmente avec l’écart d’indice entre les deux milieux formant le dioptre, la réflexion parasite sur une interface entre deux verres est moindre que la perte par réflexion air-verre, donc en combinant des doublets et des triplets collés, les ingénieurs du XIXème et du début du XXème siècles augmentent les degrés de liberté dans l’optimisation de leurs optiques, en jouant sur les paramètres dont ils peuvent disposer à volonté (indices et dispersion des verres, courbures des dioptres) en augmentant le nombre de lentilles sans trop augmenter le nombre d’interfaces génératrices de réflexions parasites.

Parmi ces combinaisons célèbres utilisant des doublets collés, il y a le Planar breveté chez Zeiss par Paul Rudolph en 1896 (figure  12), mais l’absence de traitement antireflet rend ce premier Planar peu utilisable bien qu’a priori mieux corrigé que le triplet de Dennis Taylor. En 1902, Paul Rudolph invente le Tessar, dont le succès est immédiat, le nombre de dioptres air-verre dans le Tessar est le même que dans le triplet, mais ses performances sont supérieures, et le Tessar est moins sensible aux réflexions internes que le Planar originel. Le brevet du premier Tessar expire dès les années 1920, et tous les fabricants s’appuient alors sur les principes de cette combinaison célèbre qui offre un taux de lumière parasite acceptable, comme le triplet, et une couverture de l’ordre de 50° à 60°, supérieure à celle du triplet, parfaite pour l’usage photographique général.

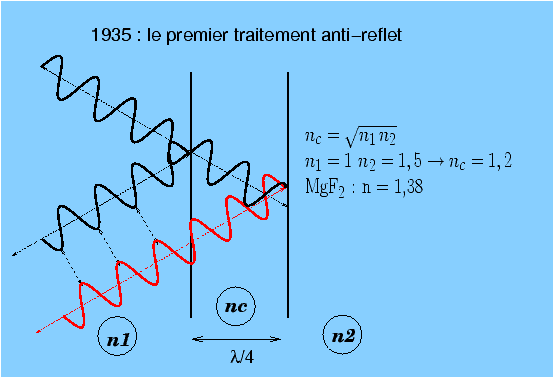
Figure 12: Il fut un temps ou le Tessar surclassait le Planar !

Le traitement anti-reflet entre en scène

En 1935, l’année même du décès de Paul Rudolph, un autre ingénieur travaillant pour Zeiss à Iéna, Alexander Smakula [11], invente le premier traitement antireflet dont le principe est rappelé sur la figure 13. Si on dépose sur chaque face de la lentille une couche mince transparente dont l’épaisseur est égale au quart de la longueur d’onde de la lumière incidente, et si l’indice de réfraction se situe à une valeur bien précise entre l’indice du premier milieu et l’indice du deuxième milieu, alors par un effet d’interférences destructives, la quantité de lumière réfléchie tombe à zéro. Pour les verres courants d’indice 1,5, il faudrait disposer d’une couche d’indice 1,22, ce qui ne correspond à aucun matériau solide connu. L’indice de l’eau est déjà de 1,33, mais il existe un oxyde transparent, le fluorure de magnésium (MgF₂) dont l’indice vaut 1,38. La longueur d’onde de la lumière jaune-vert au centre du spectre visible est de 0,55 µm, dans un milieu d’indice 1,38 cette longueur d’onde devient 0,55/1,38 = 0,4 µm environ, la couche antireflet doit donc avoir une épaisseur de 0,1 µm.

Figure 13: Principes du traitement anti-reflet

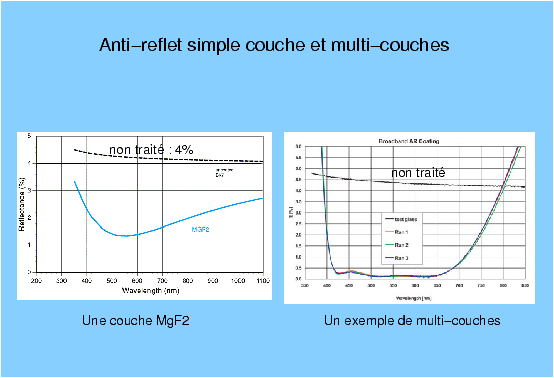
D’abord secret militaire, le traitement anti-reflet se développe rapidement pour les usages civils dès l’après guerre : dès 1949 tous les nouveaux modèles de Rolleiflex sont équipés d’optiques de chez Carl Zeiss ou Schneider Kreuznach qui sont traitées antireflet.

Le traitement anti reflet simple, monocouche, permet néanmoins avec le matériau MgF₂ de réduire le coefficient de réflexion à une valeur de l’ordre du pourcent, mais au centre du spectre visible seulement, alors que les traitements multicouches modernes réduisent le coefficient de réflexion en-dessous de 0,5% dans toutes les longueurs d’ondes utilisées par les photographes. Le traitement simple conserve néanmoins son intérêt pour les applications où l’on n’a pas besoin d’utiliser une large bande de longueurs d’onde. Les années 1960 voient se développer largement les traitements multicouches chez tous les fabricants (et chez leurs sous-traitants, sans jeu de mot), la question ne semble donc plus un enjeu technique en ce début du XXIème siècle. Néanmoins de nouveaux types de traitements basés sur des nanostructures tridimensionnelles déposées en surface des verres ont été récemment introduits [13]. L’idée de ces nanostructures consiste toujours à assurer une transition progressive entre l’air et le verre, mais au lieu d’une couche uniforme d’indice intermédiaire entre celui les deux milieux, les nanostructures de dimensions très inférieures à la longueur d’onde forment à leur façon un autre type de couche de transition dont les propriétés sont équivalentes à celles d’une multicouche, sans avoir recours à un complexe empilement de couches uniformes.

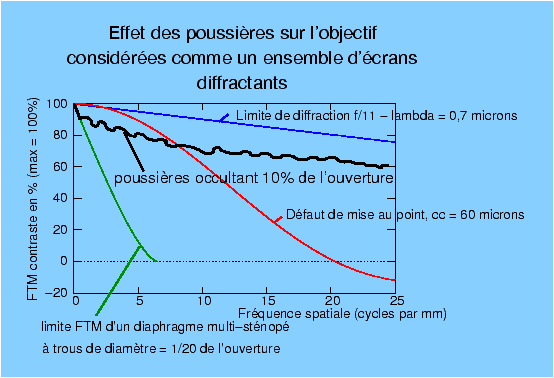
Figure 14: Couche antireflet simple couche et multicouches,
selon références [12]

Effet des rayures et des poussières

Une autre question qui préoccupe les photographes, c’est l’effet des rayures et des poussières sur les lentilles. On s’est proposé de représenter par un modèle simple l’effet des poussières absorbantes déposées au voisinage de la pupille d’un objectif parfait. En pratique les poussières se déposent plutôt sur la lentille frontale, donc assez loin de la pupille, mais les conclusions du modèle (figure 15) ne sont pas si éloignées de la réalité. Il est possible de représenter l’effet sur la courbe FTM de la présence de poussières déposées au hasard au niveau de la pupille. Sur la figure 15, on part d’une optique parfaite, limitée par la diffraction, ouvrant à f/11, par exemple un objectif de 110 mm de focale avec une pupille ouverte à 10 mm de diamètre et saupoudrée au hasard de petits disques absorbants chacun de 0,5 mm de diamètre (1/20ème du diamètre de pupille).

On s’aperçoit que dans ces conditions assez dures (10% d’occultation, c’est énorme) la perte de contraste induite par les poussières affecte, certes, toute la courbe FTM que ce soit pour les grands aplats (basses fréquences spatiales) ou les fins détails de l’image (hautes fréquences spatiales), mais finalement cet effet est beaucoup moins catastrophique qu’un défaut de mise au point ; par exemple le défaut correspondant à la limite acceptable des modèles traditionnels de profondeur de champ. Il n’y donc pas à se préoccuper outre mesure de quelques poussières occultant moins de 1% de la surface des lentilles, il vaut mieux faire attention à sa mise au point et à sa profondeur de champ !

Figure 15: Simulation de l’effet des poussières occultant partiellement la pupille d’un objectif parfait

Au passage, le modèle donne ce que serait la courbe FTM d’un multi-sténopé formé d’ouvertures disposées au hasard sur la pupille, chaque ouverture étant égale à 1/20ème de l’ouverture totale ; c’est un bon vieux problème académique, on montre que la courbe FTM résultante est exactement la même que si on avait pris un seul petit diaphragme, centré ou non, peu importe lorsqu’on utilise une optique ! La différence avec un sténopé sans lentille, c’est que pour la même qualité d’image (disons, le même flou qui semble très apprécié des sténopistes), l’image sera beaucoup plus lumineuse. Par exemple si les trous ont un diamètre égal au vingtième du diamètre de pupille, une centaine de ces trous disposés au hasard ne recouvrent que 25% de la surface. Il est donc facile de les disposer effectivement au hasard sans qu’ils ne se chevauchent, et la luminosité correspondante sera 100 fois supérieure à celle d’un sténopé unique ! Cela donne à réfléchir vu le prix fort modeste des anciennes optiques de chambre, parfois moins chères que des sténopés-de-luxe-modernes !

Piqué et contraste, ou les échanges entre physiologie et optique

Nous avons évoqué depuis le début les nuisances de la lumière parasite, peut-être est-il utile de préciser certaines notions communes en photographie : le piqué d’une image et son contraste. Ce sont des notions physiologiques, en face desquelles on peut mettre des notions d’optique et des diagrammes pour les ingénieurs, mais la situation est un peu la même qu’en acoustique physiologique (figure 16).

En musique, on définit les notions physiologiques de hauteur d’un son et du timbre d’un instrument. Une vision d’ing��nieur un peu trop rapide proposerait une correspondance simple, basée sur l’analyse harmonique des sons en régime permanent, la hauteur du son c’est la fréquence du fondamental, le timbre c’est le contenu, le poids relatif des différents harmoniques.

Figure 16

Mais les choses ne sont pas si simples [14] ; dans certains instruments comme les grands tuyaux d’orgue, le fondamental est absent ! D’autre part, un traitement numérique (assez sauvage, reconnaissons-le) qui supprime toutes les attaques (les transitoires) des notes d’un piano, transforme le son en quelque chose qui semble sortir d’un accordéon ! Enfin, certaines expériences d’électro-acoustique peuvent arriver à faire entendre à l’oreille un son qui semble « monter » indéfiniment, en jouant subtilement sur le glissement diabolique de la fréquence et de l’intensité relative des différents harmoniques issus d’un synthétiseur facétieux [15].

Cette difficulté à transcrire directement, terme à terme, les impressions physiologiques en données d’ingénieur, nous les retrouvons dans nos images : de même que timbre et hauteur d’un son s’entremêlent, de même piqué et contraste et tout ce qui nous fait juger de la qualité d’une image sont des notions pour lesquelles il est difficile de faire correspondre une et une seule notion technique. De même qu’en musique, les attaques sont indispensables à la perception du timbre de l’instrument, de même dans les photographies, l’œil est très sensible au contraste général de l’image et au contraste des bords de plages. Pour évaluer la performance des optiques et des films, les ingénieurs utilisent la notion de courbe FTM, analogue pour l’image de l’analyse harmonique des sons, et qui peut, d’une certaine façon, renvoyer au micro-contraste des fins détails et donc à la notion de piqué. Mais le fait que le contraste général d’une image (sans regarder de près les fins détails) influe fortement sur la perception de la qualité, est incontestable comme le montrent les deux images ci-dessous (figure 17) : l’image de droite est la même que celle de gauche, en termes de FTM, pour l’ingénieur c’est pareil, mais on a poussé le curseur « contraste » du logiciel de retouche vers le bas... jusqu’à l’absurde.

Figure 17

L’intérêt d’avoir un bon contraste des bords de plage n’est plus à démontrer, il suffit de voir l’utilité du curseur « accentuation » auquel il est bien difficile de résister « pour que l’image soit un peu plus percutante ! »

La lumière parasite diffuse, définition et mesure

Après ce qui pourrait apparaître, in fine, comme rien d’autre qu’une très longue introduction, acceptons sans difficulté que les réflexions parasites à l’intérieur de l’objectif et de l’appareil lui-même sont une source de baisse de contraste de l’image, donc de baisse de qualité.

Mais au fait, comment la définir, cette lumière parasite diffuse et comment la mesurer ?

Ce sera tout ce qui limite le contraste général de l’image,

• qui ne soit pas dû au voile atmosphérique,

• qui ne soit pas dû à la diffraction directe par l’iris,

• qui ne soit pas dû aux aberrations résiduelles.

Une fois ces phénomènes écartés, il reste de nombreux facteurs :

• les réflexions parasites entre le diaphragme et les lentilles,

• les réflexions parasites dans les montures ou le bord des lentilles,

• les réflexions à l’intérieur de l’appareil, dans le soufflet,

• les réflexions entre le détecteur (film, capteur) et l’intérieur de l’appareil !

Figure 18

Mesure de la lumière parasite diffuse suivant
la norme ANSI PH3.615.1980

Comment mesurer cette lumière parasite ? Pour cela nous nous appuierons sur un article du Pr. Bernard Leblanc paru dans la revue « Le Photographe » [16], article auquel nous renvoyons le lecteur pour plus de détails techniques et une bibliographie étendue.

Reprenant des travaux allemands de l’entre deux guerres, la norme ANSI PH3.615.1980 [17] donne un cadre méthodologique rigoureux pour mesurer avec précision la lumière parasite diffuse (figure 19).

On monte l’appareil ou la chambre photographique en face d’un dispositif d’illumination formé d’une sphère diffusante (analogue à l’intérieur d’une sphère intégrante [18]).

Cette sphère se comporte comme une source diffuse qui envoie des rayons de même intensité dans toutes les directions. Au centre du champ, on place un petit objet idéalement « noir », qu’il est en fait plus difficile de réaliser qu’il n’y paraît. La norme spécifie que la luminance de cet objet doit être inférieure au millième de la luminance de la sphère blanche, et ce n’est pas une mince affaire. En effet un simple coup de peinture noire n’est pas suffisant, il faut fabriquer un véritable piège à lumière avec des chicanes censées interdire tout espoir de ressortir aux quelques rayons qui s’y aventureraient malencontreusement. Ce point noir ne doit pas être trop étendu, la norme spécifie qu’il doit être vu depuis l’objectif sous un angle ne dépassant pas 1°.

On place dans l’appareil, à l’endroit où se forme l’image, un photo détecteur de dimensions suffisamment petites pour ne prendre en compte que l’image du point noir sur la sphère.

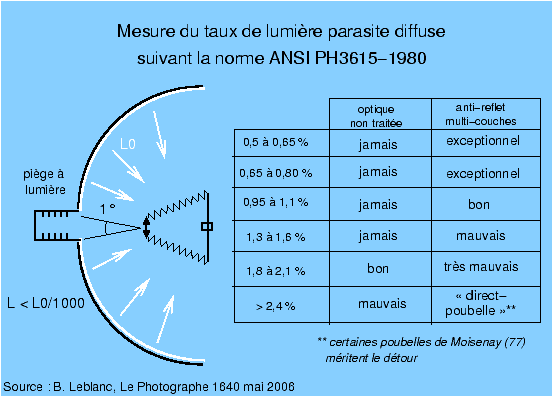Figure 19

Idéalement, pour prendre en compte les réflexions parasites sur le film lui-même, il faut laisser le film en place et, par exemple, le percer pour laisser passer le photo détecteur avec sa connectique depuis l’arrière. Percer le détecteur, facile à dire avec du film, plus difficile à faire avec un capteur silicium ! B. Leblanc [16] donne la valeur de 25% pour le coefficient de réflexion diffus du film, c’est une valeur qui surprend, on se rend compte qu’on a photographié dans ces conditions depuis des décennies sans beaucoup plus de tracas que cela !

Le photo détecteur enregistre les éclairements produits dans l’image ; idéalement les éclairements sont proportionnels aux luminances des objets [16], logiquement si la luminance du point noir est 1/1000ème de la luminance du fond blanc, l’éclairement détecté dans l’image du point noir devrait être égale au millième de l’éclairement donné par le fond blanc.

En réalité à cause de la lumière parasite diffuse, ce rapport entre les éclairements qui devrait ne jamais dépasser le millième est de l’ordre du pourcent, c’est à dire que ce qui est mesuré dans l’image de la tache noire est en fait dû en majorité à l’accumulation de lumière parasite issue du fond blanc ; cette lumière tombe là où elle ne devrait pas, et sa contribution devient prédominante par rapport à ce qui est effectivement émis par le petit objet noir lui-même.

Négligeant la contribution propre du point noir, la mesure du rapport entre l’éclairement dans les hautes lumières de l’image et les basses lumières (image du point noir) donne un taux de lumière parasite dont les valeurs typiques sont données sur la figure 19. Les meilleures optiques sont affectées d’un taux de lumière parasite qui ne descend que très rarement en dessous du pourcent, les bonnes optiques se situant autour du pourcent.

Figure 20

En d’autres termes, sans lumière parasite diffuse, le contraste de l’image, défini comme le rapport entre les éclairements de l’image du fond blanc et l’éclairement dans l’image du piège à lumière (figure 20), ce contraste devrait être rigoureusement égal au contraste de l’objet. Plus le sujet et contrasté, plus le taux de lumière parasite est élevé, et plus le contraste de l’image s’affaiblit par rapport au contraste du sujet. L’effet de la lumière parasite diffuse est dont de plus en plus important pour les sujets à contraste élevé.

On peut définir un facteur de perte de contraste sous la forme suivante [16] :

Ce facteur de perte est toujours supérieur à l’unité, selon le taux de lumière parasite, il va de 2 à 3 pour les sujets de contraste moyen (figure 20) (rapport de luminances de 1 à 125) mais peu dépasser 10 pour des sujets à fort contraste, sujets qu’on peut toutefois enregistrer avec un film négatif couleur moderne capable « d’encaisser » un écart de luminances de l’ordre de 10 diaphragmes (1 à 1000).

Une situation moins catastrophique qu’il n’y paraît...

Après avoir décrit les effets nuisibles de la lumière parasite, suivons les conseils de B. Leblanc [16] qui nous incite à prendre le bon côté des choses : cette réduction du contraste a en fait un effet compensateur (figure 21) tout à fait analogue à l’effet d’une pré lumination. Il est raisonnable de penser que les densités enregistrées sur un film sont identiques selon que les luminations sont obtenues en une seule fois ou en deux fois [19], c’est à dire : image du sujet plus lumière parasite enregistrées simultanément, ou en deux fois successives, voile de pré lumination suivi de l’exposition par l’image du sujet sans lumière parasite. Nous renvoyons à l’article de B. Leblanc pour une discussion plus approfondie sur les courbes de noircissement avec et sans lumière parasite diffuse [16].

Tout ce qui vient d’être dit concerne aussi, bien entendu, les appareils munis d’un capteur silicium. Avec des difficultés supplémentaires liées au pouvoir réflecteur a priori élevé des capteurs dont la surface, polie optiquement, est génératrice de réflexions spéculaires alors que la surface d’un film est plutôt diffusante. Là encore un traitement antireflet semble indispensable sur le capteur lui-même, B. Leblanc note que les constructeurs d’appareils et de dos numériques communiquent assez peu sur cette question des réflexions parasites dans leur matériel !

Figure 21

Conclusions

Au terme de cette discussion, nous pouvons résumer la situation de la façon suivante :

• La lumière diffuse est un élément essentiel du paysage : on ne sautait imaginer la photographie d’extérieur sans la grande variété des phénomènes de diffusion de la lumière. Néanmoins le succès des photos de paysages de l’Ouest américain n’est pas étranger à la sécheresse de l’air, limitant ainsi le voile atmosphérique toujours présent en Europe de l’Ouest.

• Dans l’appareil photographique lui même, il faut constater que malgré près d’un siècle et demi de progrès des objectifs, des verres, des procédés de fabrication mécanique, des couches antireflet et des peintures absorbantes, la lumière parasite est toujours présente à un taux de l’ordre du pourcent. Cet effet qui semble difficilement « compressible » au-delà des limites actuelles a tout de même un avantage de compenser les contrastes extrêmes, par exemple en photo de paysage.

Figure 22

Une autre piste de réflexion, si on peut dire, consiste à accepter l’idée suivante : à partir du moment où l’on réfracte la lumière pour lui faire former une image du monde qui nous entoure, il y a nécessairement une portion de cette lumière qui devient lumière parasite. Et l’homme invisible, s’il existait (figure 23), devrait n’être source d’aucune lumière parasite ; pour cela, il faudrait que les systèmes optiques qui lui serviraient à voir le monde qui l’entoure ne réfractent, ne diffractent et ne diffusent aucune lumière. Ce qui serait à la fois fort difficile à réaliser et fort difficile à vivre. Sur ce point, nous renvoyons les lecteurs à la mise en scène particulièrement pertinente que proposent sur ce sujet grave les artistes Suisses Plonk & Replonk [20].

Figure 23

Enfin, on pourrait chercher une solution technique, imaginer un appareil photo qui serait totalement immunisé contre la lumière parasite. Là encore, l’imagination d’un artiste Suisse [21] nous guidera dans cette proposition d’un appareil de facture classique, mais qui serait le seul à être immunisé totalement contre la lumière parasite (figure 24).

Figure 24

Références

[1]

La colombe légère lorsqu’elle fend d’un vol rapide et libre l’air dont elle sent la résistance pourrait croire qu’elle volerait mieux encore dans le vide.
Emmanuel Kant, dans la Critique de la raison pure.

[2]

Le coefficient global de réflexion (albédo) de la surface lunaire est donné entre 7% et 12% selon différentes sources. Au niveau des « mers », le sol lunaire est plus sombre, avec un coefficient de réflexion inférieur à 10% (7-8%). Le sol lunaire où ont été prises les photos de la NASA est donc nettement plus sombre qu’un gris photographique à 18%. Pour s’en convaincre il suffit de se rappeler que le diaphragme correct pour exposer la pleine lune, un objet éclairé par le même soleil brillant que les objets terrestres en plein été, est de l’ordre de f/8 à f/11 (au 1/125s à 125 ISO) alors que la même « règle de seize » suggère... f/16 pour le gris moyen à 18%.

http://www.dil.univ-mrs.fr/gispert/enseignement/astronomie/2eme_partie/planetes/lune.php

[3]

Le modèle expliquant le diffusion de la lumière par les molécules est crédité à Lord Rayleigh (1842 - 1919).

http://fr.wikipedia.org/wiki/Diffusion_Rayleigh

[4]

http://fr.wikipedia.org/wiki/Polarisation_(optique)

[5]

René Descartes (1596 - 1650) reprend les lois de la réfraction énoncées par son prédécesseur Willebrord Snell van Royen ou Snellius (1580 - 1626). En réalité, ces lois étaient –dans leur forme la plus simple du passage de la lumière entre l’air et un milieu transparent comme l’eau– connues des mathématiciens Arabes Ibn Sahl (Abu Sa‘d al-‘Ala’ ibn Sahl) (940 - 1000) et Ibn Haitham (965­1040)

Snell : http://fr.wikipedia.org/wiki/Willebrord_Snell

Ibn Sahl : http://en.wikipedia.org/wiki/Ibn_Sahl

Ibn Haitham : http://unesdoc.unesco.org/images/0014/001412/141236E.pdf

[6]

La propagation de la lumière en ligne droite dans un milieu transparent suppose un milieu homogène. Les exceptions concernent les effets de mirage par suite de la non homogénéité des indices de réfraction de l’air dans une ambiance de température non-homogène, ou bien lors de la propagation dans milieu transparent d’indice variable comme une lentille spéciale à gradient d’indice.

Effets de mirage, le rayon vert : http://fr.wikipedia.org/wiki/Mirage

http://fr.wikipedia.org/wiki/Rayon_vert

Utilisation du gradient d’indice dans une lentille, principes :

http://www.univ-lemans.fr/enseignements/physique/02/optigeo/stiglent.html

[7]

Dennis Taylor était le chef ingénieur opticien chez Cooke à York en Angleterre. Le triplet fut breveté en 1893 et équipa des centaines de milliers d’appareils photo jusqu’aux années 1960, il équipe encore aujourd’hui de nombreux projecteurs.

http://en.wikipedia.org/wiki/Cooke_triplet

[8]

Dans certains des premiers objectifs zoom pour le cinéma, la perte de lumière par absorption et réflexion dans l’objectif à cause du grand nombre de lentilles et des performances limitées de premiers traitements anti-reflets conduisait à indiquer sur les bagues deux échelles de diaphragmes, une échelle géométrique correspondant au diamètre de pupille d’entrée, gouvernant la profondeur de champ, et une échelle corrigée photométrique, correspondant à l’échelle géométrique décalée du facteur de transmission de l’objectif, cette deuxième échelle déterminant la pose pour un éclairage donné.

[9]

http://en.wikipedia.org/wiki/Achromatic_lens

http://wapedia.mobi/en/John_Dollond

[10]

Sur l’histoire et les progrès des objectifs photographiques, nous renvoyons nos lecteurs au livre de Rudolph Kingslake, A History of the Photographic Lens, Academic Press (1989), ISBN 0124086403

[11]

http://en.wikipedia.org/wiki/Alexander_Smakula

[12]

Traitement anti reflet mono-couche MgF₂

http://www.escoproducts.com/html/single_layer_mgf2_coatings.html

http://www.escoproducts.com

Traitement anti reflet multi-couches

https://www.omegafilters.com/index.phppage=tech_DMRS

https://www.omegafilters.com

[13]

Traitements anti-reflets basés sur des nano-structures :

http://imaging.nikon.com/products/imaging/technology/scene/20/index.htm

http://www.canon.com/news/2008/sep17e.html

[14]

Émile Leipp, Acoustique et musique, Masson, 1984, ISBN 2225801967

[15]

Sur les sons « paradoxaux », nous renvoyons aux travaux du Pr. Jean-Claude Risset

http://auriol.free.fr/psychosonique/ClefDesSons/ParadoxesJCR.htm

[16]

Bernard Leblanc, Le Flare, rayons lumineux intempestifs, « Le Photographe », N° 1640, mai 2006

http://www.lephotographe.fr

[17]

Norme ANSI PH3.615.1980 Method of testing veiling glare of still-picture camera objectives

[18]

http://fr.wikipedia.org/wiki/Sph%C3%A8re_int%C3%A9grante

[19]

Dans la plupart des films il n’y a pas, ou très peu, d’effet d’intermittence, c’est à dire que sous réserve que la lumination totale reste dans les limites de la réciprocité du film (la non-réciprocité implique un allongement des luminations aux très longs temps de pose à faible éclairements), l’enregistrement en une seule fois d’une lumination donnée conduit au même noircissement que l’enregistrement de N poses successives indépendantes de lumination 1/N. En principe la même chose devrait s’appliquer aux détecteurs électroniques basés sur l’effet photo-électrique, à ceci près qu’un temps d’attente trop long entre plusieurs poses ajoute un courant d’obscurité qui remplit de charges les photo-sites en l’absence de lumière incidente.

[20]

Les soucis optiques de l’homme invisible, selon Plonk & Replonk :

http://www.plonkreplonk.ch/html/cartes/grandes_cartes/063.jpeg

http://www.plonkreplonk.ch

[21]

Voir la bicyclette double de Denis Bigler, artiste Fribourgeois :

http://www.st-denis.ch/sculpture/zDosSculpture/tourDeVis/niv2tourDeVis.html

http://www.st-denis.ch

dernière modification de cet article : 2008