|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

l'auteur
Télécharger l'article
|
Formulaire d’optique géométriqueEmmanuel Bigler Table des matièresIntroductionLa pratique des appareils photo tout automatiques, dont le teléphone portable représente peut-être un exemple emblématique dans la pratique photographique en ce début du XXI siècle, éloigne naturellement le photographe des vieux principes de la formation d’une image optique, et lorsqu’il passe au moyen format ou à la chambre, et a fortiori lorsqu’il se lance dans une construction personnelle –ce que le grand format permet de façon passionnante– se posent de nombreuses questions auxquelles le forum de discussion galerie-photo.info essaie de répondre : déplacement d’une image au passage à travers une lame de verre, montage possible ou pas de courtes ou de longues focales sur une chambre donnée, utilisation et distances de mise au point possibles avec des bonnettes ou des tubes-allonge, etc... mais de fait toutes les réponses découlent des bases de l’optique géométrique traditionnelle et de quelques formules simples et « bien connues ». Bien entendu, il est de règle de pratiquer le moyen format ou le grand format sans jamais faire appel aux formulaires et schémas des cours académiques ! Le lien purement manuel, visuel et tactile du photographe avec un appareil dépourvu de tout automatisme semble a priori peu compatible avec une espèce de démarche intellectuelle qui voudrait tout modéliser et tout calculer par avance... Mais par ailleurs le nombre de questions fréquemment posées sur le forum de galerie-photo.info nous montre qu’un petit tour par les bons ouvrages et les cours de formation de base (comme ceux du CAP, par exemple) ne nuiront jamais à une pratique artistique. Le présent aide-mémoire a donc pour but d’inciter les lecteurs qui veulent aller plus loin dans leur pratique des appareils moyen format et de la chambre technique –les pratiquants des petits formats à film et des appareils numériques étant aussi les bienvenus !!– à relire les traités classiques d’optique géométique ou instrumentale et à avoir par la suite sous la main le présent article pour retrouver rapidement une formule ou un schéma. Bibliographie
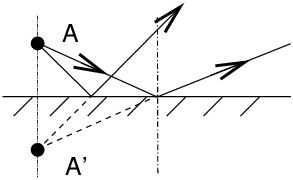
I Miroirs plansA’ est symétrique de A par rapport au plan du miroir
II Miroirs sphériquesFormules paraxiales algébriques : p. ex. CS=−SC
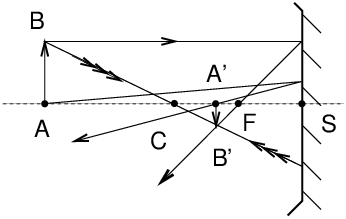
Un rayon incident parallèle à l’axe passe par le foyer F après réflexion ; un rayon passant par le centre C retourne sur lui-même après réflexion. CS=R SF=f=SC/2 formules avec origine au centre
C : 1/CA+1/CA′=2/CS
formules avec origine au sommet
S : 1/SA+1/SA′=2/SC
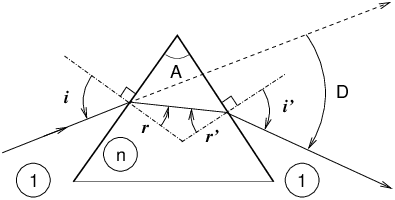
grandissement γ = −f/FA=−FA′/f FA × FA′=f2 III Prisme
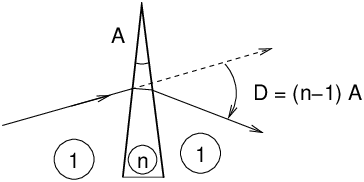
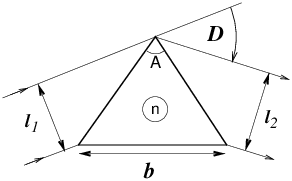
Angle au sommet A, indice n, déviation D. relations fondamentales :
Il existe un minimum de déviation dans la configuration symétrique i=i′ et r=r′ . Dans ce cas, on a
on en déduit l’indice du prisme, ce qui permet des mesures de n :
Prisme d’angle faible :
On a dans ce cas la relation approchée : D=(n−1)A. Même si le prisme est d’angle faible, et a fortiori dans le cas général, un prisme n’est stigmatique que pour des rayons parallèles en entrée, autrement dit un point-source à l’infini. Un point source à distance finie donnera une image floue en sortie. De plus en éclairage polychromatique la dispersion des couleurs empire encore le phénomène. Dispersion : l’indice n dépend de la longueur d’onde λ, et donc D dépend de λ.
Sachant que dn/dλ dépend du verre, on peut écrire
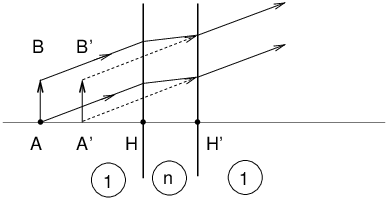
dD/dn peut être calculé géométriquement et vaut b/l2. IV Lame à faces parallèles
Exemple : air/verre : n=3/2 AA′ ~ 1/3 HH′ V Dioptre sphériqueFormule de Lagrange-Helmholtz :
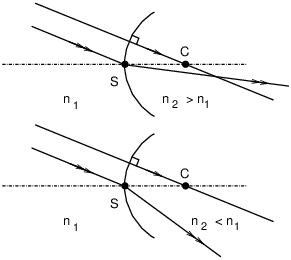
Dans un dioptre sphérique :
Formules avec origine au sommet :
Formules avec origine au centre (noter le croisement d’indices par rapport au cas précédent) :
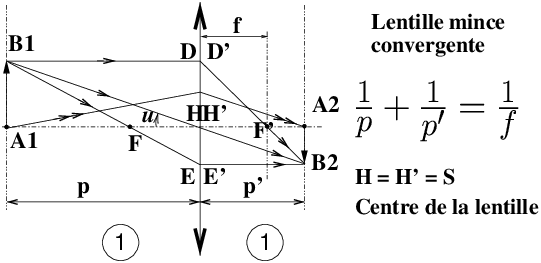
VI Lentilles mincesVI 1 Convergentes :Formules de Descartes « arithmétique » (toutes grandeurs positives) pour les applications de type prise de vue photographique ou projection de diapositives ou de transparents avec objet réel A1 et une image réelle A2 :
Pour que la conjugaison objet-image puisse se faire, on montre qu’une distance minimum objet-image est nécessaire :
Exemples : pour faire une projection avec une lentille convergente de 250 mm de focale ; il est impossible de « faire la netteté » s’il y a moins de 1m entre l’objet et l’écran. Pour un projecteur de diapositives 24×36 équipé d’une optique de focale 90 mm cette distance est ramenée à 360 mm. À la distance minimum A1 A2 = 4 f on est au rapport 1:1 qui a peu d’intérêt pour une projection (sauf pour un transport d’image avec renversement dans un instrument), mais ce qui correspond à la situation de macrophoto avec l’image aussi grande que l’objet. En prise de vue cette configuration dite « 2f-2f » correspond au rapport 1:1 (image = objet) ce qui permet de photographier un timbre-poste plein cadre en 24×36. Par rapport à la prise de vue courante, objet à l’infini, il faudra donc rallonger la distance objectif-film d’une distance égale à la focale, à l’aide d’une ou plusieurs bagues-allonge ou d’un soufflet (voir plus bas « focométrie »). VI 2 Formules algébriques généralesPour tout système centré, dans l’approximation de Gauss.
Formules de Descartes généralisées avec origines aux plans principaux H et H′ ; s’il faut ne se souvenir que d’une seule formule algébrique, valable dans tous les cas (objets réels ou virtuels, lentilles convergentes ou divergentes, association de lentilles minces ou épaisses) c’est celle-ci :
où C désigne la convergence du système, avec :
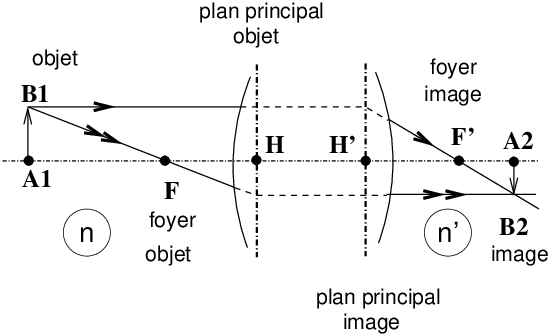
Les points principaux H et H′ sont les points de l’axe optique situés dans les plans principaux. Les plans principaux sont des plans objet/image conjugués avec un grandissement égal à +1. On trouve les plans principaux en cherchant l’intersection d’un rayon parallèle à l’axe avec le rayon émergent correspondant (ceci détermine le plan principal image passant par H′), ou d’un rayon émergent parallèle à l’axe avec le rayon incident correspondant (ceci détermine le plan principal objet passant par H). Grandissement :
Formules de Newton généralisées :
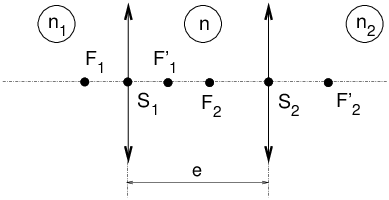
Points nodaux N et N′ : les points nodaux d’un système optique sont deux points de l’axe optique, conjugués l’un de l’autre et pour lesquels les rayons correspondants croisant l’axe en ces points font le même angle (rapport de convergence des rayons égal à +1). Pour les sytèmes optiques à milieux d’entrée et de sortie identiques (par exemple : dans l’air) les points nodaux sont confondus avec les points principaux, soit N=H, N′=H′. Dans un tel système le plus courant, les distances focales objet et image sont égales et opposées soit : HF = −H′F′. Un système à milieux extrêmes identiques n’a donc qu’un seule distance focale, f′=H′F′ qui est positive pour un système convergent et négative pour un système divergent. VI 3 Association de deux lentilles mincesConsidérons l’association de deux lentilles dans des milieux extrêmes d’indices n1 et n2, avec un milieu intermédiaire d’indice n.
Soit C1 et C2 les convergences de chacune des deux lentilles :
La convergence C du système centré résultant s’écrit suivant la formule de Gullstrand :
Remarque : la position des plans principaux H et H′ peut être absolument quelconque et sans rapport avec la position des centres des deux lentilles. Cas particulier : deux lentilles minces dans l’air avec e=0 (lentilles accolées) ⇒ C=C1+C2 VII FocométrieVII 1 Méthode de Cornu
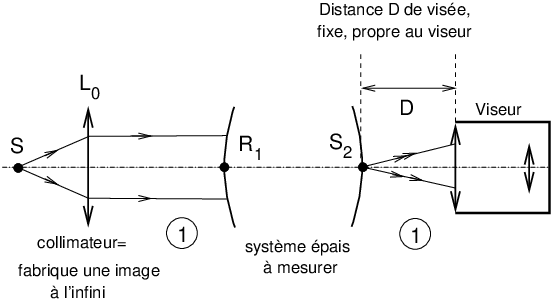
La source S est au foyer de la lentille L0. On forme ainsi un collimateur.
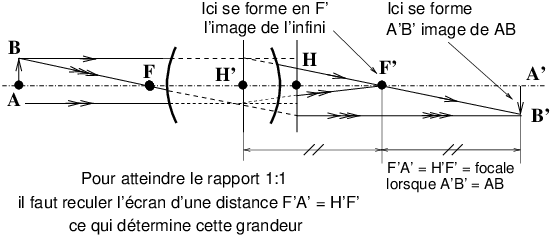
VII 2 Méthode simplifiée pour les systèmes convergents.Cette méthode est connue dans les traités français d’optique instrumentale sous le nom de méthode de Davanne & Martin (fin du XIX siècle).
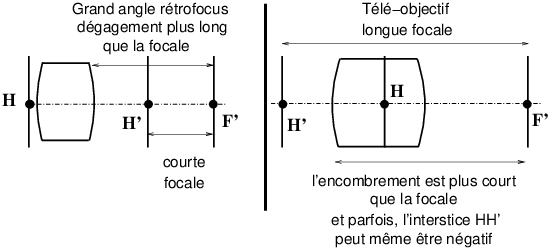
Remarque : le dessin représente H derrière H′, c’est une situation parfaitement possible pour un système épais.
Cette méthode est typiquement applicable au cas des objectifs pour appareils photo.
VIII Instruments visuels classiquesVIII 1 OeilL’œil « normal » (ou « emmétrope ») voit net sans accommoder à l’infini.
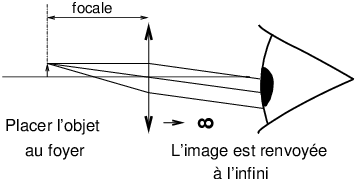
VIII 2 LoupeL’objet est au foyer ⇒ l’image est renvoyée à l’infini.
Le grossissement intrinsèque « commercial » de la
loupe est défini par : Gic=1/4f′,
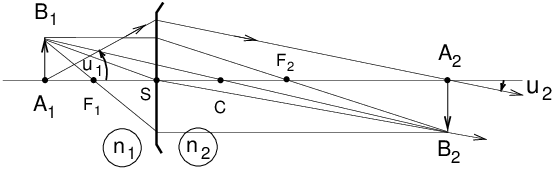
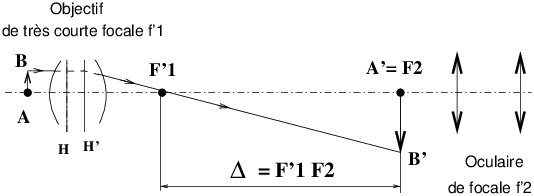
où f′ est la focale en mètres. VIII 3 Microscope
A B′ est l’image agrandie de A B. L’objectif du microscope est un système centré de très forte convergence (très courte focale f′1, de quelques mm à 1 cm). L’oculaire est un autre système convergent qui renvoie à l’infini l’image A′ B′ donnée par l’objectif. Dans ces conditions on peut voir net sans accommoder. La distance Δ = F′1 F2 ~ 16 cm (longueur de tube) dans les microscopes classiques (ceux utilisés en biologie). On définit la puissance P du microscope par : P~ Δ/f′1 f′2. Le grandissement γ (pour l’objectif) s’écrit γobj.=Δ/f′1. Le grossissement « commercial » du microscope s’écrit Gcm=γobj.× Gocul.. Les ordres de grandeur sont : Gcm de 25 à 2500, γobj. de 2,5 à 120, et pour les oculaires Gocul. de 5 à 20. VIII 4 Lunette astronomique
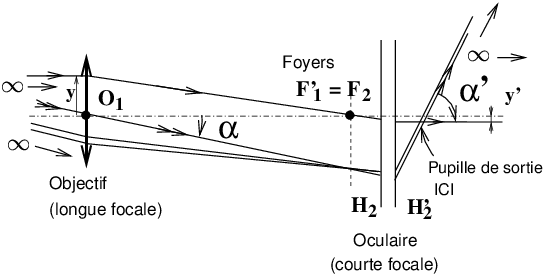
La lunette est dite réglée afocale ou ∞−∞ si F′1 et F2 coïncident. Dans ce cas le grossissement angulaire G s’écrit :
Pour un système centré afocal, le grandissement transversal γ est indépendant de la position de l’objet. Ce grandissement s’écrit :
Exemples de valeurs : f′1=1 m, f′2=2 cm ⇒ G=-50 (signe - car l’image est renversée). VIII 5 Jumelles terrestresUne paire de jumelles est équivalente à deux lunettes astronomiques couplées, associées à des prismes redresseurs en vue de remettre l’image « dans le bon sens ». Signification des indications commerciales : 8 × 20 signifie : 8 pour le grossissement angulaire (sans unité) et 20 pour le diamètre de l’objectif exprimé en mm. Au-delà de G ~ 10 on ne gagne plus rien pour une utilisation à main levée à cause du flou de bougé. 2 En divisant le diamètre de l’objectif (p.ex. 20 mm) par le grossissement (p.ex. 8) on obtient le diamètre de la « pupille de sortie » c.à.d le diamètre du faisceau lumineux juste en sortie de l’oculaire, soit 2,5 mm dans l’exemple choisi. Pour une utilisation des jumelles de jour, une pupille de sortie de 2,5 mm suffit. Avec des jumelles 8 × 50, la pupille de sortie sera de 6,25 mm ce qui n’est utile que pour une utilisation de nuit. En effet le jour la pupille de l’œil ne dépasse pas un diamètre de 2,5 mm environ, c’est donc elle qui limite le diamètre du faisceau : inutile de payer fort cher une 8 × 50 dans ce cas. De nuit en revanche la pupille d’œil étant ouverte de 6 mm de diamètre au moins, on bénéficiera d’un effet ’d’entonnoir à lumière’ très utile pour l’observation des étoiles 3. VIII 6 Annexe : Réglage des instruments pour éviter la fatigue visuelleBUT : s’assurer que l’image observée est « loin devant » et non pas entre 1 et 20 cm... ce qui conduit à une accommodation forcée, d’autant plus gênante lorsque les deux yeux n’observent pas à la même distance, parce que l’instrument est déréglé. Pour tous les instruments binoculaires, il est primordial de régler correctement l’écart pupillaire, aucun opérateur n’étant fait de la même façon ! Les oculaires modernes à grand champ permettent de conserver les lunettes correctrices ; c’est important, en particulier pour la correction d’astigmatisme qui ne peut être obtenue que par les verres ophtalmiques. Une myopie ou une hypermétropie faibles, dépourvues d’astigmatisme seront par contre aisément compensées en retouchant le réglage de netteté central et la correction dioptrique de l’un ou l’autre oculaire (voir ci-dessous).
————————————————————
Voir les autres articles sur www.galerie-photo.com Des questions ?
dernière modification de cet article : 4 Novembre 2019
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||