|
|
|||||||||||||||||||||||||||

l'auteur
Télécharger
|
Tables de profondeur de champ en macrophoto
|
||||||||||||||||||||||||||
|
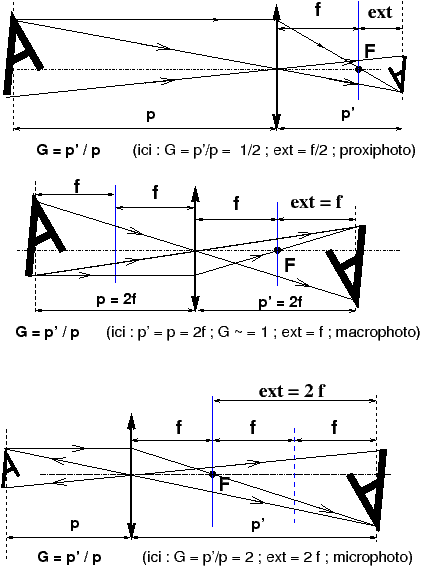
Figure 1: Proxi-, macro- et microphoto peuvent être définies partir des valeurs du grandissement G ou de l’extension de soufflet ext = G f |
1.2 Profondeur de champ
On appellera profondeur de champ totale l’intervalle de distances p2 − p1 (figure 3) dans lequel une tranche de l’objet doit être située pour être rendue acceptablement nette sur le film ou le capteur. On peut montrer [2] que lorsque les grandissements sont plus grands que 0,1 environ, c’est à dire dans notre domaine proxi, macro et micro, la profondeur de champ totale p2 − p1 ne dépend pratiquement plus de la focale, elle ne dépend plus que du grandissement G, du réglage de la bague des diaphragmes repéré par le nombre d’ouverture N, et de la valeur choisie pour la dimension du cercle de confusion c (voir la figure 2, et pour une discussion sur la signification et le choix du cercle de confusion en fonction des différents formats de travail, on se reportera aux articles surwww.galerie-photo.com, en particulier les articles [3] et [2]).
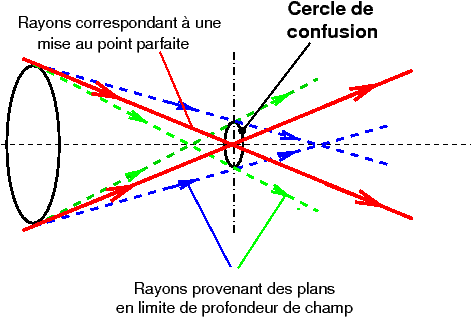
Figure 2: Au voisinage de l’image d’un point, un tracé de rayons géométrique classique est à la base des formules de profondeur de champ ; définition du cercle de confusion comme critère de netteté acceptable pour les images défocalisées : les faisceaux défocalisés provenant des points en limite de profondeur de champ se projettent sur le détecteur sous la forme d’un petit disque de même forme que le diaphragme dont on impose un diamètre maximum, le cercle de confusion acceptable c
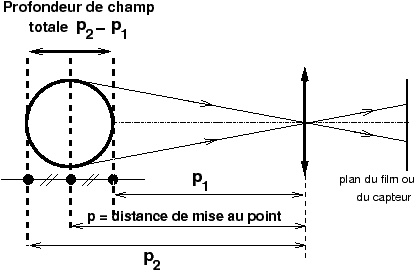
Figure 3: Définition des limites de profondeur de champ p1 et p2 au niveau de l’objet ; en macro, ces limites de profondeur de champ sont placées symétriquement en avant et en arrière de l’objet sur lequel on fait la mise au point à la distance p : p2−p = p−p1 = (p2 − p1)/2
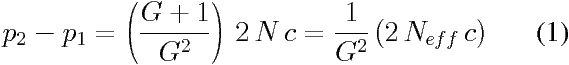
Formule de profondeur de champ totale valable en macrophoto dès que le grandissement G est plus grand que 0,1 environ.
2 Une feuille de calcul à télécharger
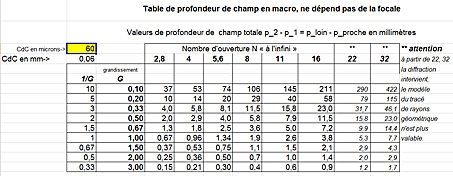
Ceux qui sont familiers avec les feuilles de calcul pourront insérer des lignes ou colonnes supplémentaires pour accéder à d’autres valeurs du grandissement G ou de nombres d’ouverture N. Outre la valeur du cercle de confusion c, on peut rentrer manuellement la valeur de l’inverse du grandissement 1/G ainsi que les valeurs des nombres d’ouverture N = 2,8 - 4 - 5,6 - ... Le reste est calculé par la feuille. Les étoiles dans les colonnes avec N = 22 ou 32 rappellent que le modèle géométrique tombe en défaut aux petites ouvertures à cause de la diffraction (voir plus bas au paragraphe 4).
N’oubliez pas d’ajuster la valeur du cercle de confusion (CdC) c en microns (case jaune dans la figure 4 ci-dessous). Par exemple c = 60 microns, c’est la valeur classique en format 6x9. De façon générale, la valeur de base du cercle de confusion est donnée par la formule :
cercle de confusion classique = CdC = c = (diagonale du format) / 1720
ce qui correspond à l’examen d’un tirage 20x25 cm vu à 30 cm avec une acuité visuelle de 2 minutes d’arc. Nous renvoyons à l’article [2] pour plus de détails sur le choix de cette valeur de c.
3 Et si on bascule ?
On apprend dans les cours de photo à la chambre que l’application d’une bascule et l’application de la règle de Scheimpflug permet « d’augmenter la profondeur de champ ». En réalité, et cela est très apparent en macrophoto, l’application d’une bascule va fortement modifier la forme de la zone de netteté acceptable autour d’un plan incliné, cette zone prend la forme d’un coin de part et d’autre du plan de mise au point incliné. En macrophoto où la profondeur de champ est très faible, ce coin est très fermé, et il ne faut guère s’attendre à des miracles si on souhaite enregistrer nettement et dans sa totalité un objet également étendu dans toutes les directions comme une sphère. Certes s’il ne s’agit que de photographier de très petits objets étagés en profondeur le long d’un plan incliné, on verra effectivement tout ce plan avec netteté si on applique une bascule selon la règle de Scheimpflug, mais pour la prise de vue d’une sphère, il n’y a hélas pas grand chose à gagner à basculer comme le montre le schéma suivant (figure 5).
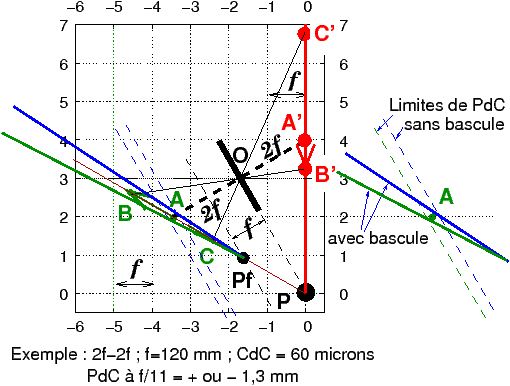
Figure 5: Détermination de la zone de netteté en macrophoto avec bascules, limites de profondeur de champ en forme de coin ; le schéma est tracé pour une optique de 120 mm de focale (un carreau de la grille = une fois la focale = 120 mm), avec un cercle de confusion de 60 microns comme pour une prise de vue en 6x9 ; on a choisi une prise de vue au voisinage du rapport 1:1 avec une bascule totale de 30° entre le plan image et le plan de l’objectif, ce qui donne un angle de 60° entre le plan objet et le plan image au rapport 1:1, 2f-2f
Tout d’abord la netteté doit être faite en respectant la règle de Scheimpflug : A’ est l’image de A sur l’axe optique, dans notre cas nous sommes au rapport 1:1, en position 2f-2f. Ensuite, le plan objet ABC, le plan de l’objectif OP et le plan imageA’B’C’ doivent se couper en un même point P qui est le pivot de Scheimpflug pour le réglage de la mise au point.
Le coin bleu dont le sommet est sur le point Pf donne la zone de profondeur de champ en coin lors de l’application d’une bascule, dans l’exemple choisi, cette bascule est très importante pour bien visualiser sur le dessin les différences avec le cas de la bascule nulle. Bien noter que le point Pf au sommet du coin est distinct du pivot de Scheimpflug P, il se situe dans le plan objet ABC à une fois la distance focale f en avant de l’objectif. Pour des prises de vue à grande distance, la distinction entre P etPf pour la construction du coin de netteté est de peu d’importance, mais en macro, au contraire, il faut évidemment en tenir compte.
La zone de netteté en coin est construite géométriquement de la façon suivante, ce qui hélas n’est absolument pas un « guide pratique »permettant de bien régler son appareil ou sa chambre dans la réalité. En macrophoto à bascule nulle, les deux plans de netteté acceptables sont situés de façon symétrique autour du plan de mise au point, la zone de profondeur de champ en macro, dans la limite de validité de l’équation (1) s’étend à part égales en avant et en arrière de l’objet (ce qui n’est pas du tout le cas à grande distance, où la zone de netteté s’étend nettement plus au-delà de l’objet visé – parfois jusqu’à l’infini – qu’entre l’objet et l’objectif).
-
on commence par tracer à bascule nulle les plans de netteté limite autour de l’objet visé, le point A ; ce sont deux plans parallèles, perpendiculaires à l’axe optique, en bleu pointillé, sur la figure 5 ; nous avons choisi une focale de 120 mm pour donner les vraies dimensions à la construction géométrique et un cercle de confusion de 60 microns comme pour le 6x9 ; dans ces conditions à f/11 avec G = 1, suivant la table de la figure 4 la profondeur de champ totale est de 2,6 mm, soit plus ou moins 1,3 mm de part et d’autre de l’objet place au point A ;
-
on trace le pivot du coin de netteté Pf à l’intersection du plan objet avec un plan parallèle au plan de l’objectif situé à une fois la distance focale en avant de l’objectif (pointillé rouge) ; de ce point Pf on trace le coin (coin bleu) dont le sommet est sur Pf et qui coupe l’axe optique à plus ou moins 1,3 mm de part et d’autre du point A ;
-
tout ce qui est contenu dans le coin bleu au voisinage des points objets A, B et C bleu sera rendu avec une netteté acceptable dans le plan image autour des points A’,B’ et C’.
Si l’objet est une sphère, et qu’elle ne rentre pas entre les deux plans de netteté acceptable à bascule nulle, on voit que l’application d’une bascule n’est d’aucune utilité, on va même perdre un peu sur le volume de la sphère qui est vu nettement si on applique une grande bascule. En revanche s’il s’agit de petits objets placés dans le plan incliné ABC, alors comme ils rentrent complètement dans le coin, ils seront vus nettement. Voir dans cet article de Michel Guigue [5] sur galerie-photo un très bel exemple de prise de vue en macro à la chambre avec une très grande bascule.
4 Diffraction et limites du modèle
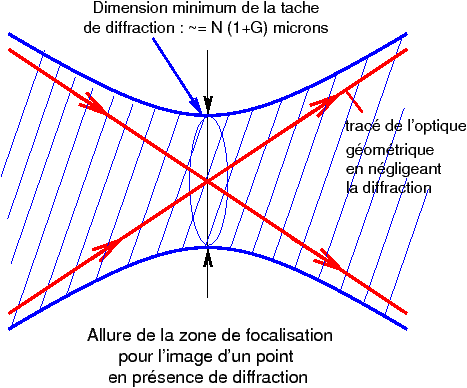
Lorsque le diaphragme est très fermé, le modèle du tracé de rayons de l’optique géométrique (figure 2) n’est plus valable à cause de l’effet de diffraction [8]. Au lieu d’une focalisation parfaite avec les rayons qui se croisent tous en un même point (ce qui, en toute rigueur, supposerait une optique dépourvue d’aberrations géométriques résiduelles), l’image d’un point ne peut pas être plus petite qu’une petite tache de diffraction, voir figure 4. Lorsque le diaphragme est très fermé, par exemple 22 - 32 - 45 ... les aberrations géométriques résiduelles deviennent négligeables devant l’effet de diffraction. On peut montrer qu’au grandissement G, le diamètre de cette tache de diffraction cdiffr vaut approximativement :
cdiffr ≃ N (1+G) microns = Neff microns
où Neff est le nombre d’ouverture effectif en macro égal à N(1+G). Pour le cas du rapport 1:1, le nombre d’ouverture et donc le diamètre de tache de diffraction sont doublés par rapport au cas infini-foyer pour une même valeur du nombre d’ouverture N gravée sur la bague. En microphoto, le diamètre de cette tache croît pratiquement en proportion directe du grandissement. Avec des valeurs de N de l’ordre de 32 qu’on peut atteindre facilement avec de nombreuses optiques macro, au rapport 1:1, la tache de diffraction est donc de l’ordre de 64 microns ! Dans ces conditions il est illusoire de se donner un critère de netteté géométrique avec un cercle de confusion de l’ordre de 60 microns, le modèle tombe en défaut. Dans la feuille de calcul on a donc rappelé que pour les nombres d’ouverture très fermés, par exemple N = 32, 45, 64, 90, etc... il faut admettre que les prévisions basées sur le modèle géométrique ne sont plus valables dès lors qu’on demande un cercle de confusion plus petit que la tache de diffraction N(1+G) microns.
Figure 6:
5 Conclusion : les compromis classiques en prise de vue macro
La recherche de la meilleure qualité d’image en photographie classique impose toujours des compromis. En photo d’action, c’est le compromis entre la vitesse d’obturation et la profondeur de champ qui est d’autant plus faible que le diaphragme est plus ouvert. Avec la possibilité en photo numérique de travailler avec des sensibilités ISO très élevées, ce compromis est devenu beaucoup moins contraignant qu’avec le film, bien que les performances des films se soient améliorées de façon considérable dans les dernières décennies (un gain d’un facteur 4 en sensibilité à granularité/résolution identiques entre les années 1970 et les années 2000).
En macrophoto, les problèmes de flou de bougé sont également très importants, à cause des vibrations [6] dont l’effet est amplifié aux grandissements élevés. L’usage de la chambre grand format en macro pose des problèmes très ardus dans la maîtrise des vibrations, mais Karl Bloßfeld [7] n’est-il pas là pour nous montrer l’exemple de façon magistrale ?
Même en supposant un montage parfaitement stable pour un sujet parfaitement statique, il reste un compromis fondamental lié à la diffraction. La profondeur de champ étant très petite, on a tendance à fermer le diaphragme le plus possible pour augmenter cette profondeur de champ. Mais au-delà d’un certain point, on va dégrader la qualité d’image par diffraction. Il est donc impossible d’enregistrer en une seule fois tout un volume en conservant la qualité d’image la plus élevée.
On peut aujourd’hui s’affranchir de ce compromis par acquisition d’images multiples à différentes mise au point étagées en profondeur, puis par post-traitement, par fusion d’images en conservant les parties les plus nettes de chaque « tranche enregistrée ». Comme beaucoup de méthodes en principe connues depuis longtemps mais impraticables avec le film, l’image numérique et les post-traitements nous permettent désormais la mise en œuvre de cette technique ... mais ceci est une autre histoire.
Annexe : formules générales de profondeur de champ
Les formules générales de profondeur de champ à bascule nulle valables à toute distance pour une optique de formule quasi-symétrique sont les suivantes (pour l’application des formules de profondeur de champ les plus générales, pour des optiques non symétriques, nous renvoyons au logiciel Calcphot de Simon Clément [4]). Si p1 est la distance limite de netteté acceptable et p2 la distance lointaine, pour une mise au point à la distance p située entre p1 et p2 on a les formules suivantes (équations (2) à (6)) :
On définit d’abord la valeur de l’hyperfocale H, à partir de la focale f, du nombre d’ouverture N (ou du diamètre de pupille d’entrée a) et du cercle de confusion c ; on en déduit ensuite les valeurs de p1 et p2 :
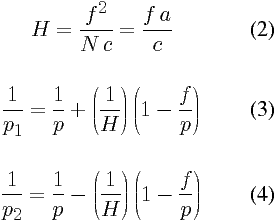
À grande distance, si p ≫ f, on peut négliger le terme correctif en f/p, (1−f/p)≃ 1 et les formules (3) et (4) se simplifient, la focale f n’apparaît plus explicitement (mais f reste contenue dans l’hyperfocale) ;
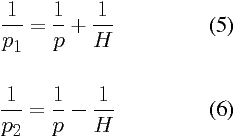
Enfin, à courtes distances, pour des grandissements G plus grands que 0,1 environ, les formules (3) et (4) prennent la forme limite de l’équation (1), avec une zone profondeur de champ qui est située symétriquement de part et d’autre de l’objet, et qui est totalement indépendante de la focale ; c’est cette formule (1) qui est utilisée dans la feuille de calcul.
Notes et Références
| [1] |
Un objectif
photographique n’est pas une lentille mince ! Introduction aux systèmes
optiques centrés épais (E. Bigler et Y. Colombe) www.galerie-photo.com/un-objectif-photo.html |
| [2] |
Décentrements, bascules et règle de Scheimpflug en petits et moyens
formats (E. Bigler) www.galerie-photo.com/decentrement-bascules-scheimpflug-petit-moyen-format.html |
| [3] |
Hyperfocale et profondeur de champ (H. Peyre)
Autres articles relatifs aux calculs de profondeur de champ
Calculateur de profondeur de champ
Feuille de calcul de profondeur de champ (E. Bigler / H. Peyre)
Profondeur de Champ et règle de Scheimpflug : une approche simple (E.
Bigler) |
| [4] |
Calcphot un logiciel dédié au calcul de profondeur de champ (S. Clément) www.galerie-photo.com/profondeur_de_champ_avec_calcphot.html On trouvera les formules de profondeur de champ générales utilisés par Simon Clément, valables même pour des optiques dissymétriques, dans lePhotographic Lenses Tutorial de David M. Jacobson. http://graflex.org/lenses/photographic-lenses-tutorial.html |
| [5] |
1er
janvier en Cambo ! une prise de vue au papier (M. Guigue) www.galerie-photo.com/premier-janvier-en-cambo.html |
| [6] | Pour une analyse très serrée des problèmes de
vibrations en macrophoto, nous renvoyons le lecteurs lisant l’anglais à ce
livre excellent, probablement l’un des meilleurs jamais écrits sur la
macrophoto : Lester Lefkowitz. The Manual of Close-Up Photography.
Amphoto. Garden City, NY. 1979. ISBN 0-8174-2456-3 (cartonné) and
0-8174-2130-0 (broché). |
| [7] |
Blossfeldt (1865/1932) un ouvrier des formes (C. Auguste) www.galerie-photo.com/karl-blossfeldt-ornemaniste.html http://fr.wikipedia.org/wiki/Karl_Blossfeldt |
| [8] |
La diffraction :
s'en soucier ou pas ? (J. M. Solichon) www.galerie-photo.com/diffraction.html |
Télécharger
- cet
article au format pdf
- la feuille de calcul
Version du 19 août 2011
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||