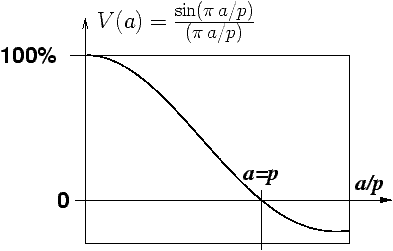|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

l'auteur
Télécharger l'article au format pdf
|
Film contre silicium :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
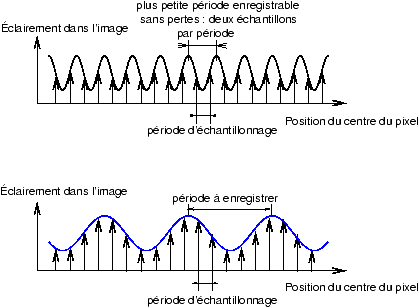
Figure 1: La règle d'échantillonnage de Nyquist-Shannon : il faut deux points pour passer une sinusoïde
Sous réserve que le son
enregistré de manière analogique avant échantillonnage ne contienne aucune haute
fréquence au-delà de ces 20 kHz (voir annexe 1
b) : « Repliement de spectre et moiré »
b)), il est possible par une opération mathématique d'interpolation (qui
peut être l'équivalent d'un filtrage passe-bas) de reconstituer le signal ou
l'image analogique d'origine.
En pratique dans le monde du son audible par exemple, on peut admettre que le
micro a une bande passante limitée à ces 20 kHz, le théorème s'applique donc, en
principe, sans problème pour un échantillonnage à 44 kHz, bien que des
fréquences d'échantillonnage jusqu'au mégahertz soient censées améliorer la
restitution du
son [4].
Certes, on peut dire également que les meilleurs microphones électrostatiques
qui font rêver les amateurs de prise de son ont une courbe de réponse
parfaitement plate montant jusqu'à 30 kHz, mais dans une technologie classique
où on serait limité à ces 44 kHz, il est toujours possible d'interposer un
filtre analogique électronique passe-bas entre le micro et l'enregistreur, on
verra qu'il peut en être de même pour l'image analogique destinée à être
échantillonnée.
Pour les images, l'application de ces principes est connue depuis les
années 1960 [5],
mais elle n'a finalement été portée à la connaissance des photographes qu'avec
le développement de la numérisation d'images sur film et la capture directe sur
silicium.
Le décompte optimiste du nombre de pixels équivalents, prenons l'exemple du 6x6,
se base sur le test des meilleures optiques avec les films à grain fin et permet
de montrer que 100 cycles par millimètre sont détectables [6],
mais à la limite, avec au final un très faible contraste sur les plus fins
détails. Il semble donc raisonnable de prendre cette limite de 100 cycles par
millimètre, soit 10 microns par cycle, comme la borne supérieure des plus fins
détails présents dans l'image analogique. Donc la numérisation de cette image
devrait se faire selon la règle des deux points par période, soit deux points
par cycle, donc il faut échantillonner avec un pas de 5 microns à 200
échantillons par millimètre, dans les deux directions en horizontal et en
vertical bien entendu. Le décompte de pixels est donc vite fait pour l'image 6x6
de 56x56mm de surface, on trouve un total de (200 x 56)2 soit 125
mégapixels. Même en 2007 avec des capteurs à 39 millions de pixels, le film ne
serait donc pas surclassé, et de loin !
Dans un très récent article du magazine « Le Photographe » [7],
Bernard Leblanc explique de la même façon qu'il avait fait ce calcul dès 1981,
en prenant 50 cycles/mm comme valeur limite, ce qui est plus réaliste, pour un
total de 8,6 millions de pixels [8]
sur une surface de 24x36mm, valeur proche du nombre de pixels d'un grand nombre
d'appareils actuels, sauf que très peu d'entre eux sont plein format 24x36, ce
qui complique un peu l'analyse.
Le paradoxe est que dans la pratique on s'est aperçu qu'il suffisait d'un nombre
de pixels nettement plus faible que prévu pour atteindre dans le tirage final,
examiné visuellement, une qualité d'image identique sinon supérieure. Par
exemple en appliquant ce calcul au format 24x36, en gardant cette limite très
optimiste des 100 cycles par millimètre, on trouve 34 millions de pixels, alors
qu'on s'accorde en ce début de l'année 2007 pour dire que les capteurs plein
format 24x36 à 16 millions de pixels surclassent les meilleures images prises
sur un film couleur de même surface.
Donc qu'est-ce qui ne va pas dans le raisonnement ? On peut faire confiance à
ceux qui ont testé les bonnes optiques pour le 6x6 [9],
et chez Carl Zeiss, une maison sérieuse s'il en est, on déclare tranquillement
des limites de résolution dépassant 200 cycles par mm pour les meilleures
optiques en vente au catalogue [10],
et on confirme des valeurs de l'ordre de 150 cycles par mm pour les meilleurs
films couleur [11].
Alors où est l'erreur ?
La règle empirique du facteur 2 à 4 équivalent en surface
Les professionnels utilisant la
capture directe d'images numériques se sont rendu compte que, lorsque l'image
est destinée, in fine, à être imprimée via une chaîne qui aujourd'hui est
entièrement informatisée et numérisée, la surface de film à passer dans un
scanner, permettant d'obtenir la même qualité que par capture d'images et
échantillonnage direct, cette surface de film devait être d'un facteur 2 à 4
supérieure à la surface de silicium donnant le même résultat [12], [13].
Les valeurs limites au contenu effectif de pixels utilisables pour une surface
de film couleur donnée (le problème est sans doute différent en noir et
blanc, où existent des films à grain extra-fin) chiffres propos��s par Henri
Gaud, valeurs plutôt sévères pour le film, sont les suivantes (je cite [13]) :
- Le [film] 24x36 [mm, couleur] atteint péniblement et dans des conditions très particulières 8 Mpixels
- Le 6x8 [cm] atteint sans trop de problèmes et avec des optiques « de course » 16 Mpixel
- Le 4x5 pouces atteint péniblement 32 Mpixels
- Le 8x10 pouces peut dans certains cas atteindre 64 Mpixels
(fin de citation)
Même en majorant ces valeurs de 50%, on reste très loin de l'estimation basée
sur 100 cycles par mm ; pour le 24X36 les 8 Mpix effectifs recoupent assez bien
l'estimation faite à partir des 50 cycles par mm comme limite du spectre de
l'image.
L'examen de ces chiffres permet de proposer une règle empirique ; sachant que
l'état de l'art actuel (début 2007, mais cela ne va pas durer !) pour les
capteurs 24x36 plein format est de 16 Mpix (dans quelques mois, ce sera sans
dout plus de 20 Mpix), pour les capteurs 4,5x6 c'est 39 Mpix, en mettant en
regard la surface de film correspondante dans la liste proposée par Henri Gaud
on voit qu'il faut numériser une surface de film au moins double pour arriver au
même résultat que par capture numérique directe. Et encore, compte tenu de
l'absence de bruit de granularité des capteurs silicium, ce facteur est
peut-être situé entre 2 et 4. Avec le facteur 2, qui est aujourd'hui
probablement très optimiste en faveur du film, on peut proposer une équivalence
entre les formats sur film et sur silicium échantillonné :
- le demi-format 18x24mm silicium ferait jeu égal avec le plein format du film 24x36,
- le petit format silicium ferait jeu égal avec le moyen format sur film,
- le moyen format silicium étant aussi bon que le 4x5 pouces,
- un dos à balayage 4x5 pouces étant aussi bon qu'un 20x25 cm numérisé.
Peut-être cette équivalence
est-elle encore conservatrice, peut-être faut-il accepter que le facteur est
plutôt de 4, auquel cas même le plan-film 4x5 pouces n'aurait plus d'intérêt [14],
mais accepter cette équivalence explique (s'il était encore nécessaire début
2007 d'argumenter sur ce point) la désaffection des professionnels pour le moyen
format à film au profit des petits formats sur silicium, 24x36... et inférieurs.
Si on ajoute tous les autres avantages en termes de productivité, la cause du
film semblerait donc indéfendable, du moins à usage professionnel mais il faut
tout de même tenir compte des problèmes d'investissement initial dans le capteur
et son système d'acquisition, plus le délicat problème du stockage/archivage des
images numériques !
Mais quelle est la limite de r��solution d'un capteur ?
Pendant la montée en puissance
des appareils numériques et des scanners en ce début de XXI-ième siècle, a été
entretenue une certaine confusion entre le nombre total d'échantillons dans
l'image, c'est à dire le nombre total de pixels (avec parfois des facteurs trois
pour certains capteurs couleur tri-couches [15])
ou le nombre de points par pouce du scanner, confusion avec la résolution de
l'image et donc l'un des éléments déterminants pour la qualité d'une image.
Pour proposer un modèle comparatif de résolution entre un film et un capteur
silicium, il faut faire quelques approximations et faire choix d'un outil de
comparaison. Nous proposons de regarder du côté des courbes de Fonction de
Transfert de Modulation (FTM) des capteurs et du film. Bernard Leblanc souligne
dans l'article déjà cité [7]
à quel point il faut être prudent en pensant que les courbes FTM contiennent
tout ce qu'il faut pour définir la qualité visuelle d'une image ; en particulier
le fait que par définition la FTM ne mesure que les faibles modulations là où on
sait que l'oeil est très sensible aux effets de bord et aux fortes modulations
dans l'image, sans oublier les effets du bruit de granularité.
Néanmoins comme on peut combiner par simple multiplication plusieurs courbes FTM
pour représenter l'enchaînement de plusieurs processus d'imagerie, et que ces
courbes sont publiées pour le film, il nous a semblé qu'un modèle simple de FTM
pour le capteur permettrait au moins d'attaquer le délicat problème qu'on peut
résumer ainsi : d'où vient ce paradoxe apparent du relativement faible nombre
de pixels (par rapport au film numérisé) nécessaires à la fabrication d'un
excellent tirage à partir d'un fichier numérique obtenu par acquisition directe
sur capteur ?
Un retour temporaire vers le microdensitomètre !
Le bon vieux microdensitomètre
va nous fournir le modèle dont nous avons besoin pour essayer de voir ce qui se
passe lorsqu'une image optique analogique est enregistrée par un capteur de type
mosaïque. Pour commencer, on va ne prendre en compte qu'une image monochrome.
Avant que les capteurs d'images de type CCD (Charge-Coupled Devices,
Dispositifs à Transfert de Charges, en français) n'existent, il était
parfaitement possible, au moins en principe, d'enregistrer sous forme
électronique une image analogique. Sans remonter jusqu'au bélinographe,
synonyme, disait-on chez les photo-reporters d'autrefois, de qualité d'image
abominable, on peut imaginer en remontant dans le temps, faire appel à une
technologie qui pourrait presque être celle des années 1930 :
- on forme l'image derrière l'objectif comme d'habitude
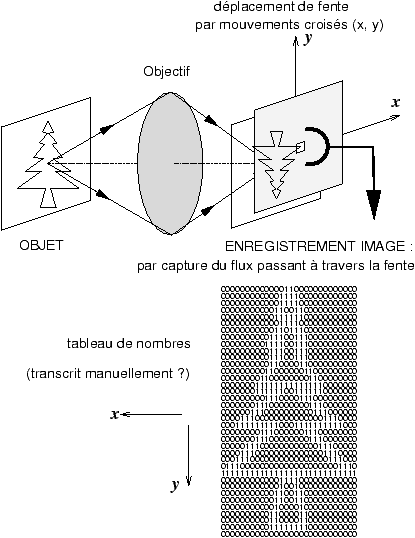
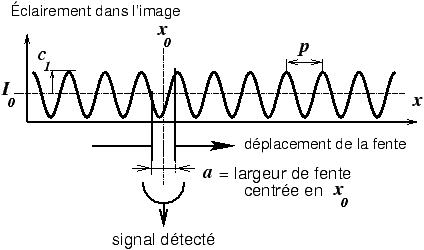
- au lieu du film on déplace une fente carrée dans tout le champ-image ; derrière la fente carrée on place un photodétecteur et pour chaque position de la fente on mesure le flux lumineux passant à travers la fente (figure 2)
Figure 2: Enregistrement analogique puis numérisation d'une image par balayage de fente... à la manière d'autrefois !
Cet mode d'enregistrement ne
correspond pas en fait au microdensitomètre parce dans cet appareil on
projette via une première optique de microscope une première fente sur le
film à analyser, et on regarde ce qui sort à travers une deuxième optique
symétrique de la première, suivie d'une deuxième fente conjuguée de la
première. Notre dispositif est donc plus simple mais il conserve du
microdensitomètre l'idée d'analyser une image optique-analogique en balayant
une fente et en faisant une mesure point par point.
En acceptant quelques progrès techniques qui nous amènent aux années 1970,
on peut imaginer, pour déplacer la fente, des mouvements croisés commandés
par des moteurs pas à pas ou par des moteurs continus asservis en position
via des capteurs de précision. Et au lieu d'un assistant de laboratoire zélé
qui noterait sur un cahier chaque valeur de flux pour chaque point après
avoir tourné les molettes d'une table à mouvements croisés manuelle, comme
on l'aurait fait dans les années 1930, un ordinateur qui pilote l'ensemble
stocke dans sa mémoire une liste des valeurs ainsi détectées dans un tableau
de chiffres à deux dimensions.
C'est à dire dans une image numérique, telle qu'on pouvait la fabriquer à
partir d'un film il y a 30 ans [1]
mais nous n'y sommes pas encore. On peut imaginer qu'un obturateur central
fonctionne à chaque prise d'échantillons, ce qui rend le processus
effroyablement lent, il serait plus astucieux de laisser se déplacer la
fente en continu, le système se comportant alors un peu comme un obturateur
à rideaux, peu importe ; cela ne change rien à notre propos qui est
d'essayer de définir une limite de résolution latérale au processus.
On suppose que le photodétecteur est bien linéaire vis à vis du flux
lumineux incident, pas de souci avec une photo-diode silicium, la linéarité
est assurée sur un facteur au moins 10000 avec les bons composants
opto-électroniques, certes c'est capital pour la sensitométrie, mais ce
n'est pas fondamental pour la question de résolution latérale de l'image.
L'opération a donc consisté à enregistrer un tableau d'échantillons, non pas
de la distribution des éclairements formés dans l'image analogique, mais une
distribution des éclairements pris en valeur moyenne sur la surface de la
fente. Or prendre la valeur moyenne de cette manière revient en fait à
échantillonner non pas l'image initiale, mais une image brouillée d'une
façon qui est parfaitement analogue à un défaut de mise au point. En effet,
si on imagine un point-objet lumineux infiniment fin et une optique
parfaite, la réponse de l'ensemble du processus de détection sera la même
lorsque la fente se déplace de plus ou moins sa demi largeur par rapport au
point d'impact de la lumière ; dans les échantillons enregistrés, on a donc
exactement la même chose que si l'image d'un point lumineux était un petit
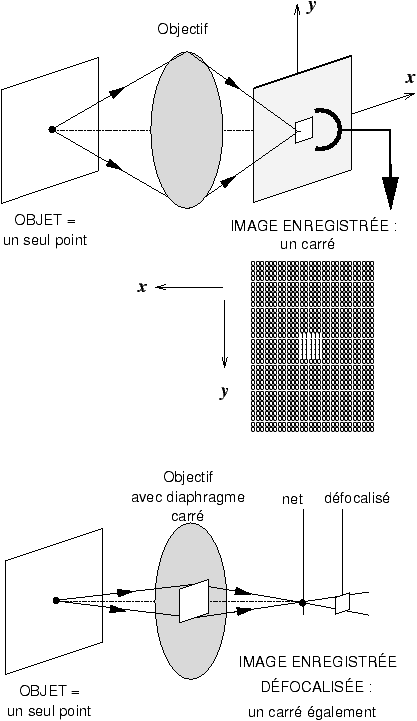
carré dont la dimension est celle de la fente. On obtiendrait le même
résultat en défocalisant une image parfaite derrière une optique munie d'un
diaphragme carré.
|
|
Figure 3: Dans le balayage de fente, l'image enregistrée d'un point est un carré égal à la dimension de fente
Donc en résumé, le processus
de détection se compose d'un effet de brouillage dû à la largeur de la
fente, suivi de la prise d'échantillons sur cette image brouillée.
Un modèle simple pour la FTM du capteur
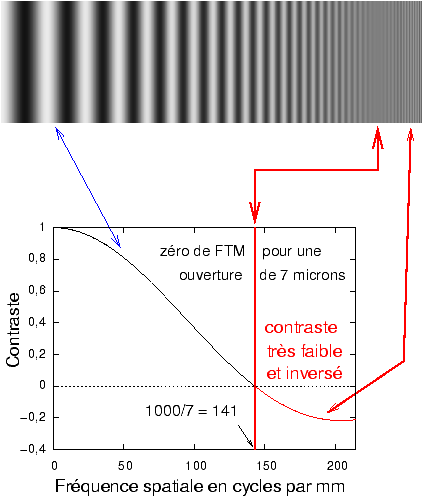
Or il est très facile de caractériser cet effet de brouillage par une courbe de FTM. Imaginons par exemple que la fente fasse 7 microns de côté, la courbe FTM correspondante se calcule classiquement (annexe 2), la courbe part de 100% de contraste à fréquence zéro et tombe à zéro pour une fréquence spatiale égale à l'inverse de la largeur de la fente soit 1000/7 = 140 cycles par mm environ (figure 4). Autrement dit, avec cette fente de 7 microns, si on regarde l'image de grilles très fines, le pas de grille le plus fin qui n'est plus détectable ce sera également 7 microns. En réalité on peut percevoir l'image de grilles plus fines que cette limite de 140 cycles par millimètre, mais avec un contraste inversé et faible, ce qui n'est pas pour arranger les choses si l'optique placée devant le détecteur est vraiment très bonne.
Figure 4: La détection d'une image analogique à travers une ouverture carrée de largeur a annule le contraste à 1000/a cycles par mm
On se reportera à l'annexe 2
b) pour la forme mathématique de cette courbe idéalisée.
Considérons maintenant un capteur silicium mosaïque monochrome idéal formé d'un
pavage de photodétecteurs carrés de 7 microns de côté, ces pavés sont supposés
parfaitement étanches à la lumière l'un par rapport à l'autre bien qu'ils soient
adjacents. Grâce aux miracles de la micro-électronique, au lieu de déplacer
péniblement notre fente unique avec son détecteur unique, par un processus qui
peut être fort complexe on admettra facilement qu'un ordinateur va être capable
de stocker le tableau ce chiffres de la même façon que dans le pénible balayage
de fente, mais l'effet de brouillage dû à l'ouverture de la fente est
exactement le même.
Retour sur l'échantillonnage
Il faut échantillonner plus fin !
On sort alors du chapeau le
théorème d'échantillonnage de Nyquist-Shannon, qui nous rappelle qu'il faut au
moins deux points de la grille d'échantillonnage pour passer une sinusoïde. Il
faut donc pour garder le plus possible des détails de l'image échantillonner
deux fois plus finement que ce zéro de la FTM dû à l'ouverture des pixels, et on
sera capable de reconstituer, non pas l'image de départ mais au moins l'image
brouillée par l'effet de fente dû à l'ouverture du pixel. En réalité c'est un
peu plus compliqué parce que la FTM d'une fente se prolonge avec une inversion
de contraste au-delà de ce premier zéro, admettons pour simplifier qu'il n'y ait
plus rien au-delà.
Pour pouvoir reconstituer l'image sans problème de repliement de spectre donc
sans perte, il faudrait échantillonner avec un pas égal à la moitié de
l'ouverture du pixel, soit 3,5 microns dans notre exemple. Dans le système à
balayage de fente, il n'y a pas de problème particulier si on possède des tables
croisées suffisamment précises, l'ouverture de la fente et la grille choisie
pour l'échantillonnage sont deux paramètres parfaitement indépendants. En
gardant la fente de 7 microns rien n'empêche de quadrupler le nombre
d'échantillons en faisant un relevé avec les tables croisées tous les 3,5
microns dans les deux directions, c'est à dire sur une grille plus fine de
fréquence 280 échantillons par millimètre.
Mais avec notre pavage en silicium avec des pixels ouverts de 7 microns, ce
n'est pas possible d'échantillonner au pas de 3,5 microns, sauf en déplaçant
d'un demi-pixel l'ensemble du capteur dans les deux directions, une possibilité
effectivement offerte par certains dos numériques et permettant de reconstituer
en plusieurs prises successives déplacées très finement l'équivalent d'une
grille de pas moitié [16].
D'autre part la surface active pour une mosaïque au pas de 7 microns, soit 140
échantillons par millimètre, a peu de chance de faire 7 microns de côté, elle
sera nécessairement plus petite. Remarquons alors que de façon un peu
paradoxale, le fait que l'ouverture des pixels soit plus petite que le pas de la
grille n'est pas gênant pour l'effet de brouillage dû à la fente, bien au
contraire : si l'ouverture du pixel n'est que de 3,5 microns, le premier zéro de
la FTM sera repoussé à 280 cycles par millimètres, autant dire que l'effet
d'ouverture du pixel va s'effacer devant d'autres effets physiques, par exemple
des fuites de lumière ou de photo-électrons d'un pixel à l'autre.
Le problème, on le voit ici, n'est pas tant dans l'effet de brouillage dû à
l'ouverture, qui intervient pour 140 cycles par mm ou plus haut, c'est qu'avec
cette grille au pas de 7 microns le théorème d'échantillonnage nous interdit de
reconstituer l'image analogique au-delà des 70 cycles par millimètre, alors que
cette image a toute chances, si l'optique est bonne, et de nombreux tests sur
mire l'attestent, de contenir des détails au-delà de cette fréquence-limite.
Un modèle de filtre anti-moiré
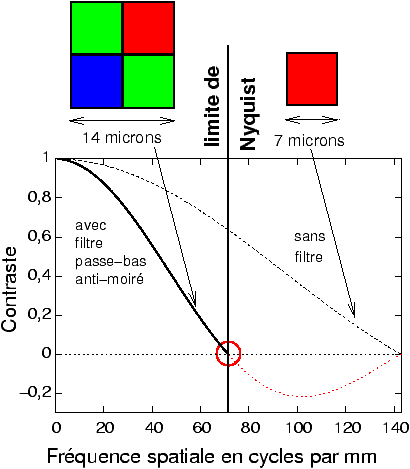
Pour éviter le repliement de spectre ou les effets de moiré, une solution consiste à brouiller l'image analogique un peu plus que ne le fait naturellement l'ouverture du pixel. C'est presque comme si lors d'un enregistrement audio on filtrait au préalable le signal analogique en sortie du micro avec un filtre passe-bas. Imaginons par exemple que par un procédé optique, on réussisse à « arroser » 4 pixels au lieu d'un seul lorsque le capteur est illuminé par un pinceau de lumière très fin. Ce qui revient à doubler l'ouverture du pixel sans changer le pas de la grille de prise d'échantillons. La FTM voit donc son premier zéro tomber deux fois plus bas (figure 5) c'est à dire dans notre exemple à 70 cycles par mm, ce qui va constituer la nouvelle limite du spectre de l'image, mais cette fois l'échantillonnage va être assez fin pour ne plus menacer par les effets de moiré l'image reconstruite ultérieurement par interpolation.
Figure 5: Un modèle simple pour la courbe FTM d'un capteur silicium échantillonné avec et sans filtre anti-moiré : si on « arrose » 4 pixels au lieu d'un, la FTM correspondant à l'effet d'ouverture doublée présente un zéro à la fréquence limite d'échantillonnage
Pour plus d'information sur les
méthodes optiques employées pour fabriquer le filtre optique passe-bas
anti-moiré, on se référera à la liste [17].
La réaction naturelle du photographe qui a toujours choisi les meilleures
optiques, et qui a fait toute sa vie la chasse aux défauts de mise au point
involontaires, c'est d'être atterré par un procédé qui revient, de fait, à un
défaut de mise au point : arroser 4 pixels au lieu d'un, c'est un effet de
brouillage à première vue insoutenable.
Mais attention. Dans le monde de l'image photographique analogique, on ne peut
que subir stoïquement les dégradations successives du contraste des fins détails
de l'image à chaque étape de la chaîne de fabrication sans pouvoir faire quoi
que ce soit. Dans le monde numérique, comme on connaît parfaitement la forme de
la courbe FTM associée au filtre anti-moiré, rien n'interdit, bien au contraire,
de retraiter le spectre de l'image enregistré pour « remonter » le contraste le
plus possible jusqu'à l'ultime limite du théorème d'échantillonnage. C'est une
simple opération mathématique équivalente à une accentuation, opération de
routine dans la préparation des fichiers pour l'impression. Il y a certainement
de multiples façons de faire cette retouche, et les constructeurs ne
communiquent pas beaucoup sur les traitements appliqués à l'image avant que le
propriétaire de l'appareil n'extraie, in fine, un fichier utilisable.
La façon dont on on aurait procédé traditionnellement par un traitement, disons,
purement académique, de Fourier linéaire (cela fut fait dès les années
1950 par traitement optique analogique [5]),
consisterait à partir du fichier échantillonné, à calculer le spectre de l'image
par une opération mathématique appelée transformée de Fourier, à
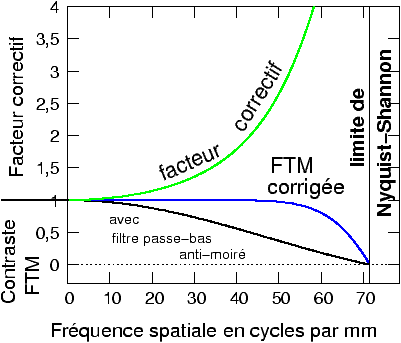
multiplier le spectre obtenu par une fonction de correction (figure 6),
puis à calculer la transformée de Fourier inverse pour re-synthétiser l'image
corrigée.
Tricherie ! s'exclameront ceux qui sont trop habitués à la photo sur film
prétendument exempte de toute manipulation ! On sait que ce genre de traitement
fut appliqué aux premières images du télescope spatial Hubble, on connaissait
parfaitement le défaut qui était principalement une aberration de sphéricité de
caractéristiques connues avec précision [18].
Mais on sait également que les images les plus belles furent obtenues après
réparation de l'optique par une mission de navette spatiale et ajout d'un
système optique correcteur.
Figure 6: Comment il est possible, en principe, en multipliant le spectre de l'image par un facteur correctif, de récupérer une partie du contraste perdu par le filtre anti-moiré
Il est clair que les
possibilités de restauration d'images intégrées dans l'appareil de prise de vue
ne peuvent que se développer à l'avenir, par exemple Hasselblad [19]
justifie un changement de format des fichiers pour le H3D par la nécessité de
tenir compte des caractéristiques de chaque optique, paramètres qui entrent en
ligne de compte avant la fabrication du fichier-image accessible à
l'utilisateur.
Comparaison avec le film couleur
Et c'est en couleurs ! [20]
Maintenant que nous avons un
modèle pour la FTM du capteur monochrome, comment passer à la couleur ?
Nous resterons très prudents. On sait que dans la majorité des capteurs, à
l'exception notable du capteur Foveon® [21]
équipant les appareils Sigma® [15],
les pixels sont arrangés en damier de type « Bayer » [22]
(figure 7).
En fait, on part d'un capteur monochrome et on ajoute sur certains pixels, soit
un filtre rouge, soit un filtre vert, soit un filtre bleu [23].
Figure 7: Principe de la
mosaïque de type « Bayer » [22],
d'après le texte du brevet original US N° 3971065, figure 6
page 4
Donc en fait on enregistre trois
images : Rouge, Verte, Bleue (RVB) sur trois grilles d'échantillonnage
entrelacées. Pour le rouge et le bleu, l'ouverture du pixel est donc au maximum
égale à la moitié de la distance effective entre deux pixels de même couleur ;
pour le vert on enregistre deux pixels en diagonale ce qui double la surface de
collection du vert. On justifie en général cette préférence pour le vert en
disant que l'oeil ayant un maximum de sensibilité dans le jaune-vert [24]
est également capable de déceler plus de niveaux de luminance au centre du
spectre visible (jaune-vert) que sur les bords (bleu et rouge).
Notons qu'au sens où on entend la périodicité d'un réseau à deux dimensions,
composé d'un motif élémentaire qui se répète dans deux directions de l'espace
(pas forcément orthogonales comme ici), la périodicité qui sous-tend la
répartition des pixels R, des deux V et du B est la même, elle est égale au
double du pas de grille de départ soit 14 microns dans les deux directions.
Quelle serait la FTM associée à deux petits carrés verts en diagonale...
difficile à dire et plus difficile encore serait de proposer un modèle de FTM
multicolore pour ce processus de détection. Dans les simulations FTM
multicolores qui sont publiées pour les objectifs, le concepteur fait choix d'un
certain nombre de longueurs d'onde où la FTM monochromatique est calculée, on
donne ensuite un résultat qui est un modèle pour la réponse visuelle en spectre
large en calculant la moyenne pondérée de ces différentes FTM pour les
différentes couleurs. Nous n'allons donc pas rentrer dans cette complexité et
nous allons pour simplifier prendre comme référence pour le capteur au pas de
grille de 7 microns les deux FTM monochromes, celle qui va jusqu'à à 70 pl/mm
avec filtre anti-moiré et celle à 140 cycles sans filtre anti moiré.
a) Quelle période d'échantillonnage pour une mosaïque RVVB « Bayer » ?
On pourrait émettre l'objection
suivante concernant le détecteur de type « Bayer » : si l'image enregistrée est
rigoureusement monochromatique, par exemple un rouge provenant d'un éclairage
laser et qui ne serait pas détecté par les pixels verts ou bleus, la grille
d'échantillonnage serait donc partiellement vide, la période d'échantillonnage
séparant deux pixels rouges étant égale au double de la période nominale, dans
notre cas : 2×7 =14 microns. Il apparaît que les constructeurs de capteurs de
type « Bayer » ou d'appareils équipés de ces capteurs annoncent effectivement un
nombre total de pixels qui est celui de tous les pixels quelle que soit
leur couleur. Est-ce illégitime ? En réalité il y a fort peu de situations
photographiques où seule une sous-grille de pixels, par exemple rouge, serait
uniquement sollicitée [25].
Donc la plupart du temps, si on imagine l'image d'une grille fine dont la
couleur est telle qu'au moins deux pixels « répondent », pour ce qui est du
théorème d'échantillonnage, la période à prendre en compte est bien la période
de la grille de base avant dépôt des filtres, soit 7 microns et non pas la
période d'un groupe de 4 pixels (R,VV,B), soit 14 microns.
Cette façon de présenter est un peu troublante si on pense à l'émission d'une
image couleur par un écran de télévision ou d'ordinateur, dans lequel il faut
impérativement compter les trois « phosphores » (R, V, B) pour constituer un
pixel.
Lorsque l'utilisateur ouvre un fichier issu d'un appareil numérique donné pour 8
mégapixels, il compte effectivement 8 millions de points affectés des trois
niveaux (R, V, B) dans son image alors que le nombre de pixels physiques de la
matrice « Bayer » correspondante n'est que 2 millions pour le rouge, 4 millions
pour les deux verts et 2 millions pour le bleu. Les valeurs manquantes sont
calculées par interpolation.
Pour simplifier la comparaison avec le film, nous accorderons donc, au bénéfice
du doute, au capteur « Bayer » dont la grille de base est au pas de 7 microns,
le fait que la limite d'échantillonnage sur un objet monochromatique, qui
devrait être en principe de 14 microns, sera considérée ici égale à 7 microns,
c'est à dire la valeur qu'on aurait en ne photographiant qu'un monde gris sans
nuances de couleurs, éclairé en lumière blanche.
En revanche dans le cas du capteur tri-couches Foveon® [15],
lorsque le nombre total de pixels annoncés par le constructeur est donné par la
somme des nombres de chaque couche, on peut réellement soulever l'objection de
la légitimité de ce décompte. En effet, si une grille « grise » est détectée par
une mosaïque « Bayer », on peut admettre que la période d'échantillonnage est
effectivement celle du réseau détecteur de base, toutes couleurs confondues.
Dans le capteur Foveon® dont le décompte nominal de pixels est de 14 millions,
en fait il y a trois réseaux superposés de 4,2 millions de pixels, tous avec la
même période de grille et tous superposés, sans le décalage latéral du capteur
« Bayer ». La période d'échantillonnage de la grille grise est dans le cas
« Foveon® » la même que pour une grille monochromatique, donc la même que pour
un capteur « Bayer » de 4,2 millions de pixels.
b) Comparaisons avec la FTM du film
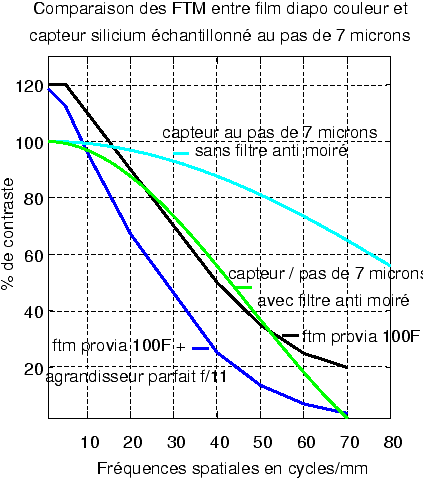
Après ce long préambule nécessaire à établir la comparaison entre le film couleur et le capteur, il est facile d'extraire des données des constructeurs la courbe FTM pour les films. On a un très bon article en anglais de Norman Koren à ce sujet [26]. Ces courbes sont en général tracées en échelles logarithmiques, nous allons ici les retracer en échelles linéaires pour rester le plus près possible du modèle proposé pour la FTM du capteur. Voici par exemple (figure 8) ce que donne la comparaison avec la FTM du film pour diapositives couleurs Provia 100F de chez Fuji ([27]) :
Figure 8: Comparaison des courbes FTM pour le film Provia 100F avec une simulation pour un capteur au pas de 7 microns : le film de petit format ne présente plus beaucoup intérêt... si on ne regarde que la résolution.
L'examen de la figure 8
fait ressortir que dans la plage de 10 à 50 cycles par mm, qui est sans doute la
plus importante pour l'examen de tirages de qualité [28],
il n'y a pas d'avantage franchement significatif du film diapo couleur moderne
sur la détection numérique directe au pas de 7 microns, même si un filtre
anti-moiré dégrade la FTM du capteur. Si on ajoute, pour le film, la perte liée
au passage par l'optique de l'agrandisseur, la FTM finale estimée en multipliant
celle du film par celle d'une optique (dans notre simulation, une optique idéale
limitée par la diffraction à 100 cycles par mm, soit entre f/11 et f/16) on
obtient au final un résultat moins bon par agrandissement optique traditionnel.
La même dégradation due à un deuxième passage par une optique s'applique
également lors de la numérisation du film dans un scanner, et bien que tous les
scanners pour film ne soient pas égaux (loin s'en faut !), on voit déjà une
première raison très simple pour qu'à surface égale, le film couleur ne soit pas
meilleur que la détection directe sur silicium.
Mais le film n'a pas dit son dernier mot, car il offre par rapport au silicium
un avantage considérable, c'est de conserver sa performance FTM sur une surface
qui n'est limitée que par les dimensions des machines servant à l'étendage des
couches sensibles. Alors que pour l'instant les difficultés pour fabriquer de
très grands capteurs silicium sont énormes, les prix (2007) restant extrêmement
élevés dès qu'on veut une surface plus grande que 39x39 mm, la norme en capteurs
photographiques professionnels étant plutôt de l'ordre de 4,5x6 cm (39x47 mm
dans l'article de Charles Cramer [14]).
Il est donc intéressant de comparer ce que la mise à l'échelle des courbes
FTM permet de conclure si on part d'un grand plan film enregistré avec une
chambre grand format, pour un rapport d'agrandissement moindre que celui
nécessaire avec le capteur silicium. Si on admet que l'image numérisée
s'agrandit à volonté sans perte, pour ce qui concerne l'agrandissement optique
classique il suffit de mettre à l'échelle la courbe FTM de l'objectif
d'agrandisseur en ramenant les cycles par mm au niveau de l'image agrandie.
|
|
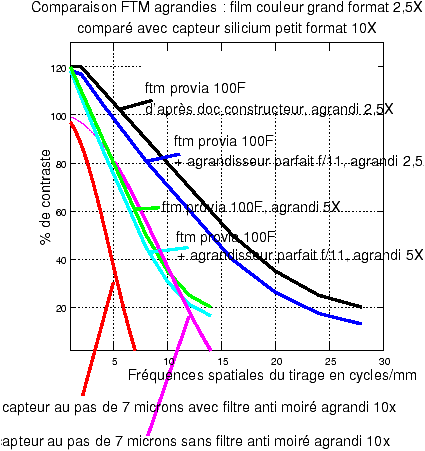
Figure 9: Comparaison des courbes FTM pour le film Provia 100F agrandi 2,5X avec une image de capteur au pas de 7 microns agrandie 10X : le film grand format l'emporte apparemment sans discussion !
Cette fois, si on tient compte
du rapport d'agrandissement moindre requis par le plan film de grand format, on
s'aperçoit qu'en termes de FTM, le film, à condition d'être agrandi 4 fois moins
que l'image numérique, l'emporte clairement sur le capteur de petit format au
pas de 7 microns. Sous ces conditions, comment se fait-il que les résultats
observés visuellement [14]
ne confirment pas cet avantage ? Qu'avons-nous oublié dans ce modèle ? Eh bien
tout simplement, en se concentrant sur l'aspect de résolution du détecteur, nous
n'avons pas pris en compte un aspect très fondamental dans l'évaluation de la
qualité d'une image, c'est à dire la question du bruit et de l'efficacité de
détection, comparées entre le film et un capteur silicium.
Cette discussion fera l'objet d'un prochain article.
Une conclusion provisoire ?
Il est
permis de rêver à ce que pourrait être la meilleure façon de coupler une optique
à un capteur échantillonné. On a vu la nécessité d'un filtre anti-moiré pour
respecter la condition de Nyquist-Shannon lorsque l'objectif délivre de fins
détails au-delà de la limite. Il existe en effet une fréquence spatiale de
coupure absolue pour toutes les optiques, c'est la limite de diffraction qui
borne vers le haut toutes les courbes FTM. Cette limite, connue depuis bien
avant l'ère de l'image numérique [5]
vaut, en fréquences spatiales, 1/(N λ) ou en période, N λ, où N
est le nombre d'ouverture de l'objectif et λ est a longueur d'onde de la
lumière. Prenant pour λ la limite effective de sensibilité de l'oeil à 0,7
microns, la fréquence de coupure de diffraction est donc en cycles par
millimètres de l'ordre de 1400/N. Imaginons que la technologie de fabrication
limite la finesse de la grille d'échantillonnage du capteur à 5 microns, cela
veut dire qu'on peut enregistrer sans aucune perte et sans risque de moiré une
image optique dont la période de coupure est de 10 microns soit 100 cycles par
millimètre. Le nombre d'ouverture correspondant à la règle des 1400/N est donc
N=14, c'est proche du meilleur diaphragme des optiques de chambre actuelles de
la classe 75°/6 lentilles prévues pour couvrir le format 9x12-4x5 pouces avec
40% de marge de décentrement.
En d'autres termes, dès aujourd'hui en déplaçant par balayage un petit capteur
avec une grille de pixels au pas de 5 microns derrière une optique de chambre
fermée à f/11-f/16, on n'a plus besoin de se soucier des effets de moiré ; seuls
risquent d'intervenir les effets de chromatisme transversal dont les nouvelles
séries d'optiques de chambre conçues pour les petits capteurs sont pratiquement
exemptes. Ces nouvelles optiques ont leur meilleur diaphragme à f/8, ce qui
donne une période de coupure ultime de 5,6 microns ; Nyquist-Shannon nous
demandent donc une grille de pixels au pas de 2,8 microns. Il est a priori
plus réaliste d'imaginer une augmentation de la surface des capteurs avec une
grille de pixels autour de 5 à 7 microns que de descendre à 2,8 microns. Reste à
savoir si commercialement le jeu en vaut la chandelle... rendez-vous dans deux
ou trois ans ?
Nous avons vu également que les problèmes de résolution et d'échantillonnage
n'expliquaient pas complètement le facteur empirique 2 à 4 en surface entre film
et silicium, il faut donc tenir compte du bruit et de l'efficacité de
détection...
à suivre !
Remerciements
Cet article fait suite à
plusieurs discussions sur le
forum technique de galerie-photo,
en particulier celle-ci, lancée par Guillaume Péronne :
http://www.galerie-photo.info/forum/read.php?f=1&i=13613&t=13613.
Nous sommes donc bien entendu redevables aux intervenants de ces discussions
pour l'élaboration des idées contenues dans cet article.
Un grand merci bien entendu à Henri Gaud pour les remarques du photographe
professionnel, en particulier pour la règle du facteur 2 à 4 équivalent entre
film et capteur silicium qu'il a élaborée après de longues heures passées à
numériser une partie de son fonds d'images sur film. Merci à Dan Fromm pour ses
objections constructives, en particulier pour avoir attiré mon attention sur les
très efficaces traitements numériques (DSP) qui permettent à partir d'un petit
capteur muni d'un filtre optique passe-bas de retrouver le plus de netteté
possible sans risquer les effets de moiré. Remerciements à Yves Colombe et
Pascal Miele pour avoir éclairé ma lanterne sur l'étrange décompte de pixels
dans les matrice « Bayer ». Merci enfin à David Giancatarina pour avoir suivi de
près les articles comparatifs cités ici entre les dos numériques professionnels
et les plan-films numérisés.
Annexe 1 : Repliement de spectre et moiré
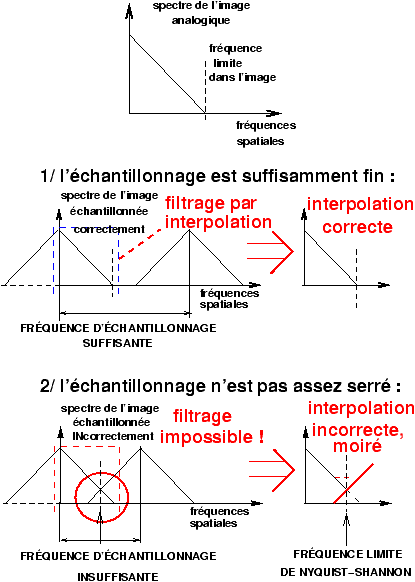
Après avoir échantillonné une image, on calcule a posteriori une estimation de l'image analogique d'origine à partir du tableau des échantillons. C'est l'opération d'interpolation. Lorsque le spectre de l'image est limité, il n'y a pas de problème à reconstituer parfaitement le spectre de l'image d'origine, et donc l'image elle-même. Lorsque le spectre de l'image s'étend au-delà de la fréquence limite donnée par le théorème de Nyquist-Shannon [2], le spectre calculé par interpolation n'est pas le spectre de l'image, mais un spectre constitué de la superposition des basses fréquences de l'image avec le repliement des hautes fréquences (figure 10).
Figure 10: Spectre d'une image échantillonnée et repliement de spectre
|
|
Figure 11: Lorsque l'échantillonnage n'est pas assez fin, le calcul d'interpolation reconstitue une sinusoïde de basse fréquence correspondant au phénomène traditionnel du moiré
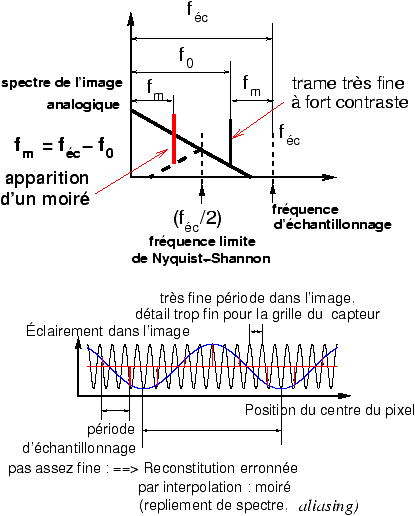
Cet effet de repliement de
spectre, appelé aliasing en terminologie anglo-saxonne est relié au
phénomène de moiré de la façon suivante. Dans le spectre faussement reconstitué,
les parties repliées sont affectées d'une fréquence qui est égale à la
différence entre la fréquence d'origine et la fréquence d'échantillonnage. Par
exemple si une grille de pas plus fin que le double de la période
d'échantillonnage est présente dans l'image, après interpolation et
reconstruction apparaîtra dans l'image reconstituée une grille de pas beaucoup
plus large, l'inverse de ce pas étant égal à la différence entre les inverses du
pas de grille d'origine et l'inverse du pas d'échantillonnage. La règle est la
même pour le moiré classique, la fréquence de moiré est égale à la différence
des deux fréquences qui se superposent, ou en acoustique, la fréquence du
battement résultant de la superposition des sons à deux fréquences émises par
deux tuyaux d'orgue différents est égale à la différence de ces fréquences.
Un exemple visuel du phénomène de moiré en imagerie numérique est proposé ici [29].
Annexe 2 : FTM pour le phénomène de brouillage par une ouverture carrée
Le problème est un classique de
l'optique instrumentale, il se posait dans les spectrographes à fente et de
façon générale dans tous les instruments où on détecte un éclairement en captant
tout ce qui passe à travers un fente de largeur donnée a. On va faire ce
calcul dans le cas d'une fente rectiligne, suivant une seule dimension d'espace
x, il se généralise facilement au cas d'une fente carrée dans le plan(x,y)
L'intensité lumineuse à enregistrer sera représentée par :
I(x) = I0(1+c1 cos(2π x /p)) (1)
où I0 est la valeur moyenne de l'éclairement, c1 un coefficient définissant une petite modulation de l'intensité de la lumière et p le pas de cette distribution, analogue à celle d'une grille mais à bords adoucis.
|
|
Figure 12: Effet de brouillage d'une distribution lumineuse sinusoïdale de période p par enregistrement derrière une fente de largeur a : si la largeur de fente devient égale à la période de la sinusoïde, il y perte totale de contraste dans le signal détecté, ce qui correspond à un zéro de la FTM.
Ce qui est détecté / enregistré, Ienr est tout ce qui passe à travers une fente de largeur a qu'on va déplacer dans la direction x, l'intensité enregistrée en un point fixé x0, qui correspond au centre de la fente, est donnée par une intégrale de la fonction d'origine prise sur la largeur de la fente :
|
Ienr(x0) = |
∫ |
|
I0 (1 + c1 cos(2 π x/p)) dx (2) |
Le résultat ce de calcul ne fait appel qu'aux fonctions trigonométriques
habituelles, et vaut :
Ienr(x0) = a I0 (1 + c1 V(a) cos(2 π x/p)) (3)
où V(a) est une fonction donnant visibilité de la
modulation, qui vient affaiblir le facteur de modulation c1,
elle vaut :
| V(a) = | sin(π a / p) | (4) |
| (π a /p) |
Le tracé de cette fonction est donné sur la figure 13,
Figure 13: Courbe FTM correspondant à l'effet de brouillage par enregistrement derrière une fente de largeur a
cette visibilité de la
modulation s'annule lorsque la condition a/p = 1, soit a=p
est satisfaite, c'est à dire lorsque la largeur de la fente d'analyse a
est égale à la période du phénomène observé p.
En termes de fréquences spatiales, le premier zéro de visibilité correspond à la
fréquence 1/a.
Si la largeur a est exprimée en microns, alors la fréquence-limite en
cycles par mm vaut : 1000/a (en microns)
Un autre résultat d'importance pour la détection, et on s'en serait douté, c'est
que le signal enregistré est proportionnel à la largeur de fente a, on a
donc un compromis entre la visibilité et la luminosité du phénomène enregistré.
Dans le cas d'un capteur silicium, la largeur de la fente d'analyse ne peut pas
être plus grande que la période des pixels ; elle peut bien entendu être plus
petite ce qui n'est pas au détriment de la visibilité des images de grilles de
pas fin, bien au contraire, mais qui est au détriment de la sensibilité du
détecteur. D'où l'usage de micro-lentilles pour collecter tout ce qui tombe sur
une surface carrée dont le côté est égal à la période des pixels. Un filtre
anti-moiré ajouté à tout cela est un dispositif supplémentaire indépendant des
micro-lentilles qui répartit la lumière non pas sur un seul pixel mais sur
quatre pixels, adjacents afin de respecter la condition d'échantillonnage de
Nyquist-Shannon, échantillonner deux fois plus fin que le motif le plus fin
présent dans l'image.
Références
| [1] |
Emmanuel Bigler, Du microdensitomètre à la photo
numérique : contribution au débat « images argentiques contre images
numériques », Mars 2002, |
| [2] |
Théorème d'échantillonnage de
Nyquist-Shannon, Wikipédia, |
| [3] |
Andrés Vega García, Mécanismes de contrôle pour la transmission de l'audio sur l'Internet, Thèse, université de Nice-Sophia Antipolis, 1996 http://www-sop.inria.fr/rodeo/avega/phd/phd-html/node10.html |
| [4] | http://fr.wikipedia.org/wiki/Super_Audio_CD |
| [5] |
Maréchal A., Françon M., Diffraction, structure des images. Influence de la cohérence de la lumière ISBN : 978-2-225-61215-2 (Masson, 1970) |
| [6] |
Christopher M. Perez, tests des
optiques pour moyen format et chambres |
| [7] |
Bernard Leblanc, Petite histoire
de la sensitométrie argentique et numérique, « le Photographe », n°
1642, juillet-août 2006, page 61. |
| [8] |
Nous désignerons ici par « pixels »
un ensemble de trois sous-pixels Rouge Vert Bleu (RVB) permettant la
prise de vues en couleurs directement, terminologie d'usage pour tous
les appareils d'amateur. |
| [9] |
Christopher M. Perez, Testing
Four Cameras, or how I learned I am completely neurotic |
| [10] |
Resolving power of photographic
films, Zeiss Camera Lens News N° 19, mars 2003 |
|
|
« Such a lens exists in the Hasselblad program. It is the Zeiss Distagon 3,5/60. In recent performance tests at Carl Zeiss it has managed to resolve up to 240 line pairs per millimeter which is far beyond the capability of today's best professional portrait films. », Zeiss Camera Lens News N°9, 2000, page 3 |
| [12] |
Réduction de format (6x7) et
conséquence optique, discussion sur le forum galerie-photo,
contribution par Henri Gaud du 22 mars 2004 |
| [13] |
Limites « raisonnables » au
nombre de pixels d'un scan-film, discussion sur le forum
galerie-photo, à l'initiative de Guillaume Péronne, 23 mars 2004 |
|
|
Voir cet article de Charles
Cramer, qui indique clairement, tests à l'appui, qu'un dos silicium 39
Mpix 39x47mm fait jeu égal avec un film 4x5 pouces numérisé avec une
machine professionnelle.
http://www.luminous-landscape.com/essays/Cramer.shtml |
| [15] |
http://www.sigma-photo.fr/site/article/affichageArticle.aspx?idSegmentation=0000014
|
| [16] |
Pour un capteur monochrome simple,
il suffirait dans le principe de déplacer l'ensemble de la mosaïque de
(0,0 ; 0, +1/2 pixel ; +1/2 pixel, 0 ; +1/2, +1/2) ce qui fait 4 prises.
En réalité pour enregistrer l'image couleur selon ce procédé, il faut,
selon le constructeur, 16 prises pour avoir la meilleure qualité d'image
possible : Sinar multi-shot digital back with micro-scanning
http://www.sinar.ch/site/index__gast-e-1778-50-1899.html |
| [17] |
Une liste de documents en ligne et
de brevets décrivant la manière de fabriquer un filtre optique passe-bas
anti-moiré. |
| [18] |
Hanisch, Robert J.; White, Richard
L., Restoration of images for the Hubble Space Telescope, Proc.
SPIE Vol. 2029, p. 194-201, Digital Image Recovery and Synthesis II,
Paul S. Idell; Ed. 11/93 |
| [19] |
Lire dans la revue promotionnelle Hasselblad,
« Victor by Hasselblad », numéro 1, hiver 2006, l'article sur la
correction des aberrations par post-traitement numérique. On n'attachera
pas, à la lecture de l'article, trop d'importance à cette lentille en
apparence mince qui souffre de chromatisme transversal... en effet, si
on peut blâmer la lentille pour ses nombreux défauts, il y a en a un
dont elle est exempte, c'est le chromatisme transversal, propriété
qu'elle partage à son modeste niveau avec toutes les optiques
quasi-symétriques ! |
| [20] |
http://pierredac.free.fr/sketch01.htm |
| [21] |
http://www.foveon.com |
| [22] |
« Bayer », d'après le nom de
l'inventeur, le Dr. Bryce Bayer, ingénieur chez Kodak, brevet US N°
3971065, 20 juillet 1976. On lira avec profit ce très intéressant
article historique : A Brief History of `Pixel', par M. Richard
F. Lyon de chez Foveon Inc.
http://www.foveon.com/files/ABriefHistoryofPixel2.pdf |
| [23] |
La documentation Kodak, par
exemple pour le modèle KAF-39000 décrit la fa���������������������������on dont on procède pour
transformer un capteur monochrome en capteur de type « Bayer �������� : Each
of the 6.8μm square pixels are selectively covered with red, green or
blue pigmented filters for color separation.
http://www.kodak.com/ezpres/business/ccd/global/plugins/acrobat/en/ |
|
|
Le maximum de sensibilité de l'oeil selon la courbe
CIE de 1931 est donné pour 555 nm, ce qui correspond assez bien au
maximum d'émission du spectre solaire à 530 nm pour une source de
température de couleur 5500K : |
| [25] |
En réalité, l'examen des courbes
d'efficacité quantique de détection d'un capteur tel que le Kodak
K1F-39000 [23]
montre qu'une lumière rouge monochromatique à 650 nm est détectée avec
15% d'efficacité, mais qu'elle créee tout de même un signal bleu avec
une efficacité de 2% et un signal vert avec une efficacité de 3%.
Autrement dit, même une image de fine grille rouge à 650nm va donner un
signal dans le vert, avec facteur d'atténuation de 1/5, soit une perte
de 2,3 diaphragmes. Par rapport à l'étendue de mesure d'un capteur qui
est au moins de 6 diaphragmes, on voit que l'image rouge est en fait
plus ou moins détectée par tous les pixels malgré la présence des
filtres de sélection trichrome. |
| [26] |
Norman Koren, Understanding
image sharpness part 1A: Resolution and MTF curves in film and lenses,
http://www.normankoren.com/Tutorials/MTF1A.html |
| [27] |
Courbe FTM du film Fuji Provia 100
F, |
| [28] |
Carl Zeiss publie les courbes FTM
de ses optiques moyen format pour les valeurs de 10, 20 et 40 cycles par
millimètre. Pour un agrandissement au rapport 10x, cela correspond sur
le tirage à 1, 2 et 4 cycles par millimètre. On sait que pour les fins
détails observés à la distance de vision courante de 25 à 30 cm, la
limite de résolution de l'oeil est de l'ordre de 5 à 7 cycles par
millimètre (si on prend une limite de résolution angulaire de 2 minutes
d'arc par période ou soit 1/1720 radian par période discernable), donc
les valeurs 10, 20 et 40 sur l'image initial tombent après
agrandissement 10X dans une plage que l'oeil apprécie sans pertes. Une
grille de pas 70 cycles par mm agrandie 10 fois tombe à la limite de
résolution de l'oeil et aura donc a priori
peu d'influence sur la perception générale de netteté de l'image. Il
convient donc d'être très prudent, B. Leblanc rappelle dans l'article [7]
qu'à résolution égale sur les fins détails, une image plus contrastée
sur le grands aplats apparaît comme plus nette. |
| [29] |
Un exemple visuel du phénomène de
moiré en imagerie numérique |
Emmanuel Bigler 2. avril 2007
Télécharger l'article au format pdf.
dernière modification de cet article : 2007
|
tous les textes
sont publiés sous l'entière responsabilité de leurs auteurs |
|||||
|
|
|||||
|
une réalisation phonem |
|
||||
|
|
|||||