La règle de Scheimpflug :
un simple tracé de rayons
pour lycéens ?
(English Version)
Résumé: On se propose de montrer ici comment la
règle de
Scheimpflug peut être retrouvée par un tracé de
rayons élémentaire à la base de la construction des
images formées par une lentille mince convergente.
Introduction
Dans les manuels de photographie traitant des chambres grand format,
la règle de Scheimpflug
est presque toujours énoncée sans justification alors que les tracés de
rayons permettant de déterminer la position et la grandeur de l’image
d’un objet sont toujours présentés, parfois en détail. Il est vrai que
s’il fallait avoir lu avec soin ce qui est expliqué dans le brevet
original de M. Scheimpflug
[1] pour en tirer parti, il serait bien improbable
de pouvoir appliquer dans la pratique cette règle d’usage courant en
prise de vue à la chambre. Bien qu’il existe des présentations
géométriques élégantes mais très mathématiques de la « règle des trois
plans » (voir en particulier Bob
Wheeler [2] et Q.-Tuan
Luong [3],
[4]) il m’a semblé qu’un élève de lycée des années
1960 en France (les programmes ont changé depuis), à l’époque où on
enseignait l’optique géométrique en classe de première, montrerait sans
difficulté comment l’image d’un objet incliné par rapport à l’axe
optique d’une lentille se forme dans un autre plan incliné, ces deux
plans se rencontrant dans le plan de la lentille. Pour cela il suffit de
se mettre l’espace d’un instant à la place de cet élève et d’appliquer
les « bonnes règles » du cours sans trop se poser de questions.
Retrouver la règle de Scheimpflug
Dans les classes élémentaires, l’un des premier tracés de rayons que
les élèves apprennent à faire c’est la construction de l’image
A′B′
d’un objet lumineux AB formée
par une lentille mince convergente de distance focale
f. On prend toujours pour
commencer cet objet perpendiculaire à l’axe optique. Pour cela les
règles à appliquer sont les suivantes : (voir la figure
1)
- tout rayon incident parallèle à
l’axe tel que BH,
passe par le foyer-image
F′ en sortie
selon le trajet HF′B′,
- tout rayon incident qui passe
par le centre de la lentille, tel que
BO, ressort sans
être dévié suivant le trajet
OB′,
- tous les rayons émis par un
point-objet A se
croisent au point image
A′, de même pour
B et B′,
- si
AB est
perpendiculaire à l’axe, son image
A′B′
l’est aussi.
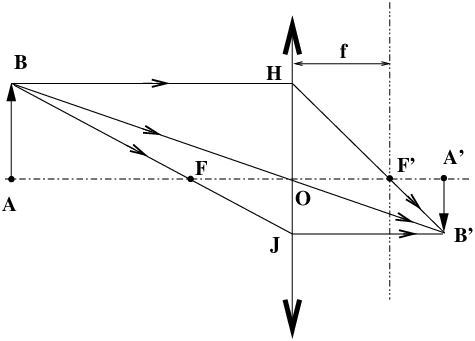
| Figure 1: Les règles classiques de construction d’une image par tracé de rayons |
Curieusement les professeurs ne proposent jamais de trouver où se
forme l’image d’un objet « incliné » tel que
CD (figure 2).
Pourtant à partir des règles précédentes on trace facilement
CIC′ (règle 1.) et
COC′ (règle 2.), puis
DKD′ et
DOD′. Jusque là rien
d’extraordinaire mais on ne voit pas du tout la relation qui peut
exister entre les plans BCD et
B′C′D′.
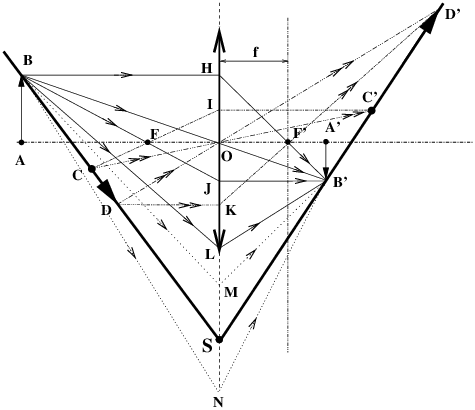
| Figure 2: La règle de Scheimpflug comme conséquence d’un tracé de rayons élémentaire. |
Il y a pourtant une autre règle que les professeurs énoncent toujours
:
règle no5
: dans tous les tracés de l’optique géométrique, on peut dilater
l’échelle verticale à volonté sans que cela ne change en rien les règles
de base, comme si la lentille était illimitée dans la direction
perpendiculaire à son axe.
Un élève discipliné tracera donc sans se poser de questions les
rayons BLB′, puis
BMB′, puis
BSB′ et même
BNB′ en conformité totale avec
toutes les bonnes règles, car tous ces rayons issus de l’objet
B devront se croiser en
B′.
Il suffit donc de dire la chose suivante.
Oublions que la lentille est limitée
(règle no5)
et considérons un rayon lumineux tel que
BCDS
; il doit donc nécessairement repasser après la lentille sur toutes les
images B′,
C′
et D′
de tous les points lumineux B,
C,
et D
conformément à la règle no3,
avec comme cas particulier que S
est confondu avec son image.
On en déduit donc que l’image d’un plan incliné
BCDS est le plan incliné
SB′C′D′,
c’est à dire rien d’autre que la règle de
Scheimpflug [1].
Remarques finales
- Une première difficulté vient de
ce qu’en pratique le diaphragme limite la lentille ou
l’objectif à un diamètre tellement petit qu’il semble
absurde de vouloir considérer un « rayon imaginaire »
tel que BCDSB′.
Pourtant, lorsqu’à partir d’un diaphragme très fermé
(rayons voisins de BOB′)
on ouvre progressivement pour permettre à des rayons
tels que BLB′ de
passer, on ne fait rien d’autre qu’obéir aux règles de
base qu’il suffit d’extrapoler selon la règle no5
jusqu’au « rayon imaginaire »
BCDSB′.
- Une deuxième difficulté provient
de ce qu’un objectif photographique est toujours un
système optique épais et non pas une lentille mince. En
fait il suffit de « découper » la figure
2 avec des ciseaux suivant le plan de la lentille
HON et d’écarter
les deux moitiés du dessin parallèlement à l’axe optique
d’une distance HH′
(positive pour un grand angle « rétrofocus » ou même
négative pour un télé-objectif) ������������gale à celle qui sépare
les plans principaux HH′
(ou les plans nodaux, ce qui est le même chose dans
l’air). L’écart entre plans principaux dans une optique
photographique ne dépasse jamais quelques centimètres.
On voit qu’en pratique cela ne changera rien ou presque
à l’application de la « règle des trois plans ».
Simplement les plans
BCDS et SB′C′D′
se couperont quelque part entre les plans principaux.
- Une dernière difficulté consiste
dans le fait que nous n’avons considéré dans cette
dérivation que des rayons qui se propagent dans « le
plan du tableau » c’est à dire un plan qui contient
l’axe optique (on appelle ces rayons : les rayons
méridiens). Qu’en est-il si on considère un
plan-objet en trois dimensions ? Là encore, un
simple tracé de rayons (fig.3) nous
donne la solution. Considérons une famille de rayons
parallèles qui se propagent suivant les lignes d’une
grille rectangulaire tracée dans le plan-objet incliné,
tous ces rayons étant parallèles au rayon
BCDS. En
appliquant une autre règle de base de l’optique
géométrique, selon laquelle des rayons incidents
parallèles entre eux se croisent en un seul point après
traversée de la lentille, ce point de focalisation
E′ étant situé
dans le plan focal, on voit facilement que le
lieu de ces rayons émergents pour une optique réglée
suivant la règle de
Scheimpflug
est effectivement un autre plan incliné dans
l’espace. Ce plan-image incliné coupe le « plan du
tableau » (figure 2) selon le
rayon méridien SB′.
Une conséquence intéressante de ce tracé de rayons dans
l’espace est de montrer très simplement comment l’image
d’une grille-objet parfaitement rectangulaire tracée
dans le plan-objet incliné sera dans le cas général
rendue distordue dans le plan-image incliné
sous la forme d’une grille trapézoïdale, et
ceci indépendamment de la netteté point par point qui
elle est parfaitement conservée lorsque la règle de
Scheimpflug
est respectée.
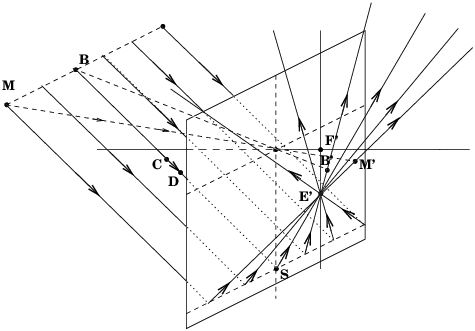
| Figure 3: Tracé de rayons dans l’espace pour les plans conjugués au sens de la règle de Scheimpflug |
Sources et Références
Voir les autres articles sur
www.galerie-photo.com
Des questions ?

