[abonnement gratuit]
the author
|
Emmanuel Bigler is a professor (now
retired) in optics and microtechnology at ENSMM, Besançon, France, an
engineering college (École Nationale Supérieure d'Ingénieurs) in
mechanical engineering and microtechnology.
He got
his Ph.D. degree from Institut d'Optique, Orsay (France).
E. Bigler
uses an Arca-Swiss 6X9 FC view camera.
Mail

|
|
|
Depth of field and Scheimpflug's rule :
a minimalist geometrical approach
(Version Française)
Emmanuel BIGLER
ENSMM, 26 chemin de l'Epitaphe, F-25030 Besancon cedex,
FRANCE, e-mail :
Mail
Résumé : We show here how pure geometrical
considerations with an absolute minimum of algebra will yield the
solution for the position of slanted planes defining the limits of
acceptable sharpness (an approximation valid for distant objects) for
Depth-of-Field (DOF) combined with Scheimpflug's
rule. The problem of Depth-of-Focus is revisited using a similar
approach. General formulae for Depth-Of-Field (DOF) are given in
appendix, valid in the close-up range. The significance of the circle of
least confusion, on which all DOF computations are based, even in the
case of a tilted view camera lens and the choice of possible numerical
values are also explained in detail in the appendix.
Introduction
We address here the question that immediately follows the application of
Scheimpflug's rule: when a camera is properly focused for a pair of
object/image conjugated slanted planes (satisfying "Scheimpflug's
rules of 3 intersecting planes''), what is actually the volume in object
space that will be rendered sharp, given a certain criterion of acceptable
sharpness in the (slanted) image/film plane?
Again the reader interested in a comprehensive, rigorous, mathematical study
based on the geometrical approach of the circle of confusion should refer to
Bob Wheeler's work [1]
or the comprehensive review by Martin Tai [2].
A nice graphical explanation is presented by Leslie Stroebel
in his reference book [5], but no details
are given. We re-compute in the appendix Stroebel's
DOF curves and show how they are related to the classical DOF theory. The
challenge here is to try and reduce the question to the absolute minimum of
maths required to derive a practical rule.
It has been found that, with a minimum of simplifications and sensible
approximations, the solution can be understood as the image formation
through the photographic lens fitted with an additional positive or negative
"close-up'' lens of focal length ± H, where H is the
hyperfocal distance. This analogy yields an immediate solution to the
problem of depth of field for distant objects, the same solution as
documented in Harold M. Merklinger's work [3],
[4], which appears simply as an
approximation of the rigorous model, valid for far distant objects.
1 Derivation of the position of
slanted limit planes of acceptable sharpness
1.1 Starting with reasonable
approximations
Consider a situation where we are dealing with a pair of corresponding
slanted object and image planes according to Scheimpflug's
rule (fig. 4), and let us first assume a few
reasonable approximations:
-
first we neglect the fact that the projection of a
circular lens aperture on film, for a single, out of focus point object,
will actually be an ellipse and not a circle. This is
well explained by Bob Wheeler [1]
who shows, after a complete rigorous calculation, that this
approximation is very reasonable in most practical conditions.
-
second we consider only far distant objects; in other
words we are interested to know the position of limit surfaces
of sharpness far from the camera, i.e. distances s or p
much greater than the focal length f. We'll show that those
surfaces in the limit case are actually planes, the more
rigorous shape of these surfaces for all object-to-camera distances can
be found in Bob Wheeler's paper, in Leslie
Stroebel's book [5], and here in
the appendix.
-
finally we'll represent the lens as a single positive
lens element; in other words we neglect the distance between the
principal planes of the lens, which will not significantly change the
results for far distant objects, provided that we consider a
quasi-symmetrical camera lens (with the notable exception of telephoto
lenses, this is how most view camera lenses are designed).
1.2 A "hidden treasury'' in classical
depth-of-field formulae !
Let us restart, as a minimum of required algebra, with the well-know
expressions for classical depth of field distances, in fact the ones used in
practice and mentioned in numerous books, formulae on which are based the
DOF engravings on classical manually focused lenses.
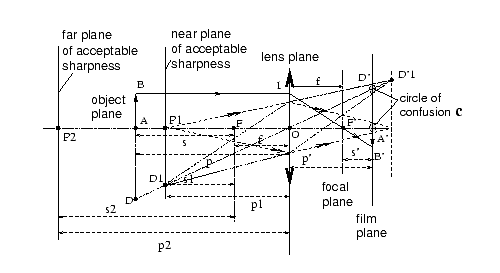
Figure 1 : Depth-of-field distances
s1,
p1 and s2,
p2 for a given circle of confusion
c
Consider an object AB perpendicular to the optical
axis, let p1 and p2
the positions (measured from the lens plane in O) of the planes of
acceptable sharpness around a given position of the object p.
It should be noted (see fig. 1) that the ray tracing for
a couple of points outside the optical axis like D1
and D'1 yields in the image plane
A'B' an out-of-focus image of circular shape (not an
ellipse, as it could be considered at a first); this out-of-focus image
is exactly the same as the circular spot originated from P1;
this is simply the classical property of the conical projection of a
circular aperture between two parallel planes. The out-of-focus spot near D' is centred on the median ray
D D1 O D' D'1
that crosses the lens at its optical centre. This point will be important in
the discussion about transversal magnification factors for out-of-focus
images.
Assuming a given value for c, the diameter of the circle of
confusion, p1 and p2
are identical whether we consider AA' on-axis or DD' off-axis
and is given, for far distant objects, by
In eq.(1), H is the hyperfocal distance for
a given numerical aperture N and diameter of the circle of confusion
c, defined as usual as
The previous expressions of eq. (1) are valid only for
far-distant objects; readers interested by more exact expressions, valid
also for close-up situations, will find them below in the appendix.
Now let us combine eq.(1) with the well-known
object-image equation (known in France as Descartes
formulae), written here with positive values of p and p'
(the photographic case)
Combining equation (1) into (3) yields
the interesting formula (4)
which is nothing but the object-image equation for the image
A'
located at a distance p' of the lens centre O, but as seen
through an optical system of inverse focal length (1/f+1/H)
for the near plane p1
(point P1) and (1/f-1/H)
for the distant plane p2
(point P2). The
expression (1/f+1/H) is simply the inverse 1/f1
of the focal length of a compound system made of the original lens, fitted
with a positive close-up lens of focal length H.
When you "glue'' two thin single lens elements together into a
thin
compound with no air space, their convergences (inverse of the
focal length) should simply be added. Thus in a symmetric way (1/f-1/H)
is nothing but the inverse 1/f2 of
the focal length of a compound system made of the original lens, fitted with
a negative "close-up'' lens of focal length -H.
1.3 A positive or negative "close-up''
lens to visualise DOF at full aperture?
1.3.1 a classical DOF rule revisited
Before we proceed to the Scheimpflug case, let us
examine the practical consequence of the additional close-up lens approach
in the simple case of parallel object and image planes. We'll show how this
additional lens element will allow us to revisit some well-know DOF rules
(figure 2).

Figure 2 : When the an additional
"close-up'' lens of positive or negative power +H or -H allows us to
find well-know DOF rules
It is known to photographers that when a lens is focused on
the hyperfocal distance H, all objects located between H/2 and
infinity will be rendered approximately sharp on film, i.e. sharp within the
DOF tolerance. Consider a lens focused on the hyperfocal distance and let us
add a positive close-up lens element of focal length +H. The ray
tracing on figure 2 shows that the object plane
located at a distance H/2 is now imaged sharp on film if the lens to
film distance is unchanged. In a symmetric way, the same photographic lens
fitted with a negative "close-up'' additional lens element of focal length -H
will focus a sharp image on film for objects located at infinity. The same
considerations actually apply whatever the object to lens distance might be,
in this case formulae (4) are simply a more general rule
valid for any object to lens distance p; the result is eventually the
same, i.e. the positions of acceptable sharpness p1
and p2 are located where the film
"would see sharp'' through the camera lens fitted with a positive or a
negative "close-up'' lens of focal length +H or -H.
1.3.2 DOF visualisation at full
aperture??
It would be nice to be able to use this trick in practice to check for depth
of field without stopping the lens down to a small aperture. In large format
photography, f/16 to f/64 are common, and the brightness of the image is
poor; it is difficult to evaluate DOF visually in these conditions. The
close-up lens trick would, in theory, allow to visualise the positions of
limit planes of acceptable sharpness at full aperture simply by swapping a +H
or -H supplementary lens by hand in front of the camera lens with the
f-stop kept wide open.
There is no reason why this could not work from an optical point of view.
Unfortunately classical close-up lenses are always positive and, to
the best of my knowledge, my favourite opticist round the corner will not
have in stock eyeglasses with a focal length longer than 2 metres (a power
smaller than 0.5 dioptre). The shop will probably have all kinds of positive
and negative lenses in stock, but none, even on special order, will exhibit,
say, a focal length of 10 metres (1/10 dioptre) because this is quite
useless for correcting eyesight.
In large format photography, the hyperfocal distance is always greater than
2 metres. For example a large format lens, with a focal length of 150 mm,
for which we consider appropriate a circle of confusion of 100 microns has
an hyperfocal distance smaller that 2 metres only when closed down at a
f-stop smaller than f/112. An impossible aperture, and moreover for such
"pinhole'' kind of values, diffraction effects make the classical DOF model
questionable.
Let us however see if this could work in 35mm photography. Shift and tilt
lenses do exist for 35mm SLR cameras. Consider a moderate wide-angle of 35
mm focal length and assume that the circle of confusion is chosen equal to
the conventional and widely used value of 33 microns. The hyperfocal
distance is equal to 2 metres at f/18: this is a more realistic value. Those
who use shift and tilt lenses, 35mm focal length on a 35mm SLR can actually
use a +0.5 or -0.5 dioptre supplementary lens to get an idea of the DOF
planes at f/16-f/22 without actually stopping down the lens. And we'll show
below that this will be useful also for moderate tilt angles.
For large format photographers, actually the majority of users of tilts and
shifts, the trick of a positive or negative "close-up'' lens will only be a
very simple geometrical help to determine where the slanted planes of
acceptable sharpness in object space are located, as explained now.
1.4 Where Mr. Scheimpflug helps us
again and gives the solution
When the film plane is tilted, the ray tracing is similar to the one on
figs.1 and 2, but the object
plane is slanted (figures 3 and 4).
We show now that even in this case, we can also consider the camera lens
fitted with a positive or negative close-up lens to determine the object
planes of acceptable sharpness.
1.4.1 a last argumentation without
analytical calculations...
Now a subtle question that arises is: we now have the formula connecting the
longitudinal position of out-of-focus pseudo-images (actually:
elliptical patches, close to a circle, when the tilt angle is small) in the
slanted film plane with the corresponding longitudinal position of a point
source in the object space. But what is the transversal
magnification factor? To find this we need an additional diagram (figure 3).
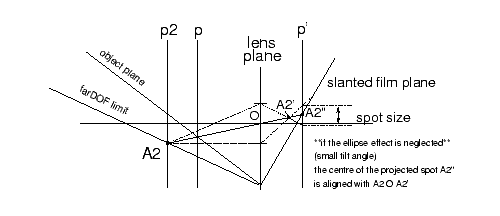
Figure 3 : The transversal magnification
factor for an out-of-focus pseudo-image, p'/p2,
is the same as for a true image through a compound lens
Due to basic properties of a geometrical projection of
centre O, if we neglect the "ellipticity'' of the DOF spot,
the centre of the out-of-focus image, A''2,
is aligned with the median ray A2 O A'2.
Hence, the transversal magnification factor for an out-of-focus image A''2
is the same as a for a true image when A''2
is formed "sharp'' through a compound lens fabricated by adding a thin
supplementary lens to the camera lens. This transversal magnification factor
(see fig. 3) is equal to p'/p2,
the same value would be obtained for A2''
as a true image through the compound lens.
So both in longitudinal and
transversal position the
correspondence between the object space and the image space for out-of-focus
images is exactly the same as if viewed "sharp'' through the compound lens.
Applying basic rules of true object-image formation we already know
that the image of a slanted plane is another slanted plane, we do not need
any analytical proof to derive what follows.
1.4.2 ...and Mr. Scheimpflug gives us
the solution without any calculation!!
As a consequence, without any further calculations we apply
Scheimpflug's rule to the compound optical system and
we
conclude that the limit surfaces of acceptable sharpness for distant objects
are the slanted conjugate planes of the film plane with respect to a
compound, thin lens centred in O, with a focal length equal to f1
(for p1) or f2
(for p2), and that all
those planes G1 P1
and G2 P2
intersect together in S with the slanted object plane AS and
the slanted Scheimpflug-conjugated image plane S
A' as on fig.4.
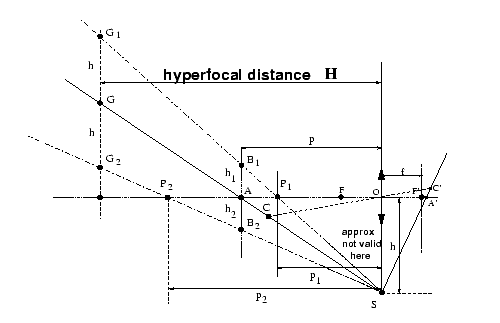
Figure 4 : Position of slanted planes of
acceptable sharpness, for distant objects, according to this simplest
model: fit the original lens with "close-up'' lenses of focal length (±
H)
To actually define where those planes are located, we simply
have to impose that they should cut the optical axis at a distance p1
(point P1) or p2
(point P2), respectively. Then,
simple geometric considerations on homothetic triangles P2
A B2 vs. P2
O S as well as B1
A P1 vs. S O
P1
combined with eq.1 yield the interesting and most simple
final result: with h=OS, both distances h1
and h2 are equal to
Now consider a plane G1
G G2
perpendicular to the optical axis and located at the hyperfocal distance H
from the lens plane (fig.4). Considering homothetic
triangles G1 G S vs.
B1 A S and G
G2 S
vs. A B2 S, we
eventually get
a nice result given by Harold M. Merklinger in
ref.[4]. Note that for far distant objects,
the image point A' on the optical axis is located very close to the
image focal point F'; thus the distance h, hard to estimate in
practice, can be computed from the "camera triangle'' O
S A'
from the focal length f and the estimated tilt angle OSA' as:
tan (O S A') ~ f/h. For small tilt angles tan(O
S A') ~
sin(O S A'), which eventually yields the same result as
in reference [4], where the diagram is
drawn with a reference line perpendicular to the film plane (hence
a sine instead of a tangent) instead of the lens plane like
here.
2 Application to the problem of
Depth-of-Focus
Another classical photographic problem is the determination of Depth-of-Focus. The question is:
for a given, fixed, object plane,
what is the mechanical tolerance on film position in order to get a good
image, within certain acceptable tolerances? The following (figure 5)
yields the solution, at least to start with the case of an object plane
perpendicular to the optical axis and an image plane parallel to the object
plane.

Figure 5 : A ray tracing similar to the
ones used in the Depth-of-Field problem yields the solution of the
Depth-of-Focus problem
If p' denotes the film position for an ideally sharp
image of an object plane at a distance p, the two acceptable limit
film plane positions p'1 and p'2
are given by
|
p'1
= p'(1+ |
|
) ; p'2 =
p'(1- |
|
) (7) |
In order to keep the derivation as simple as possible and keep the
equivalence with a true optical image formation valid, we need an additional
but reasonable approximation, namely that the hyperfocal distance H
is much greater that the focal length f. This is what happens in most
cases and is argumented in the appendix. Within this approximation, it is
found (see details in the appendix), not so surprisingly, that the limit
positions p1 and p2
as defined above for the Depth-of-Field problem are approximately the
optical conjugates of the positions p'1
and p'2 of the
Depth-of-Focus problem through the photographic lens of focal length f,
as given by Descartes formula
Combining this eq.(8) with the transversal
magnification formula p1'/p
or p2'/p, still the same for
pseudo-images (the centre of out-of-focus light spots) as for real images,
we find that in the general case of a slanted object plane, for far
distant objects (so that equation (1) is valid), the limit positions for the image planes in the Depth-of-Focus problem are
given by two slanted planes, those slanted image planes of acceptable
sharpness being the optical conjugates (through the lens of focal
length f) of the slanted object planes in the Depth-of-Field problem.
Hence, applying Scheimpflug's rule, we conclude
again that those slanted planes intersect together at the same point S
(see fig. 6)
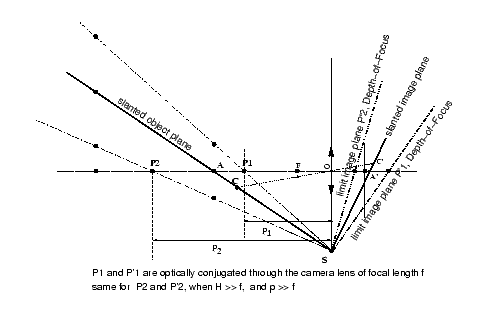
Figure 6 : For a slanted object plane
AC
located far from the lens, and when the hyperfocal distance is much greater
than the focal length, the image planes of acceptable sharpness SP1'
and SP2' in the Depth-of-Focus
problem are the optical conjugates of the slanted Depth-of-Field object
planes SP1
and SP2 through the camera lens
Appendix : depth of field formulae also valid for close-up,
reasonable limits for the choice of the circle of confusion c
Depth-of-Field formulae valid for close-up
>From Newton's object-image formulae s×
s'=f× f = f2
it is not too difficult (although rather lengthy) for an object AB
perpendicular to the optical axis to derive more general formulae giving the
position p1 and p2
of the planes of acceptable sharpness around a given position of the object
p
(as measured from the lens plane, see fig.1).
Those exact formulae (9) and (10)
are used in a html-javascript [7] and a
downloadable spreadsheet [8] on Henri
Peyre's French web site. Another derivation, strictly equivalent, is
proposed by Nicholas V. Sushkin [6]
offering an in-line graph.
There is however a restriction: those formulae will be also valid for a
thick compound lens where the pupil planes are located not too
far from the nodal planes identical to principal planes in
air. This is the case obviously for a single lens element or a cemented
doublet, but also for quasi-symmetric view camera lenses; however for
asymmetric lenses or more generally speaking for a lens where pupil planes
are far from nodal planes, an extreme case being, for example, so-called telecentric lenses, this classical depth-of-field approach is no longer
valid. Another ray tracing diagram has to be taken into account; of course
depth-of-field will increase when stopping down such a lens, but this will
not be quantitatively
described by equations (9) or (10).
Assuming a given value for c, the diameter of the circle of
confusion, a derivation not shown here yields the following (and
surprisingly simple) result, which is presented in a slightly different but
strictly equivalent form by Nicholas V. Sushkin on his web site [6]
|
|
|
= |
|
+ |
|
(1- |
|
) ; |
|
= |
|
- |
|
(1- |
|
) (9) |
these formulae can be also written as
where (see fig.1) f is the focal length of the
lens (here considered as a single, positive, thin lens element) p the
position (measured from the lens plane O) of the object plane AB,
assumed to be perpendicular to the optical axis.
Then p1 is the position of the
near
limit plane of sharpness and p2 the
position of the far limit plane of sharpness. It should be noted in
eqs.(9), that all distances p, p1,
and p2 are (positive) distances
measured with respect to the lens plane plane O. Here, for a
thin positive lens, O is identical to the principal planes. No
problem with a thick compound lens if pupillar planes are not too far from
principal planes, re-starting from the single thin lens element you just
have to "separate'' "virtually'' the object side from the image side by a
distance equal to the (positive of negative) spacing between principal
planes.
Definition of the "true'' hyperfocal distance
Let us first point out that there is a subtle difference in what appears as
the "true'' hyperfocal distance when exact formulae are used. If one tries
in (9) or (10) to find the proper
distance p for which p2 goes
to infinity, the value of H+f is found instead of H in
the conventional approach. In this case, the near limit of acceptable
sharpness will be Htrue=(H+f)/2.
In practice as soon as H is much greater than 5 f, the
difference is not meaningful. It could be possible to re-write equations (9)
and (10) as a function of Htrue,
but we eventually prefer to denote by hyperfocal distance the
well-accepted value H=f.f/N.c since it
naturally comes out of the computation, and as it is referred to in many
classical photographic books.
With this assumption on pupillar planes, the formulae given in eq.(9)
are derived from Newton's formulae within the
only, non-restrictive, reasonable approximation that the circle of confusion
c
(in the range of 20 to 150 microns) is smaller than the diameter of the exit
pupil f/N. Taking c <0.5 f/N
sounds reasonable. For example with f=100mm, the aperture diameter a=f/N
should be smaller than f/100 to be smaller than one millimetre,
whereas conventional values for c never exceed 0.5mm.
It is also possible to think again about the significance of the hyperfocal
distance H by re-introducing the value a of the lens aperture
diameter, a=f/N. The following expression is obtained:
H/f = a/c, in other words the ratio between the hyperfocal distance
H
and the focal length f is equal to the ratio between the lens
aperture diameter a and the circle of confusion c. In most
practical cases, H is much greater than f. Considering a limit
case where H could be close to f, although acceptable from a
geometrical point of view, would yield values for c that are too big
to be acceptable: for example if c can be as big as a/2,
equivalent to H=2.f, the resultant image quality will be
terrible.
Let's put in some numerical data to support this idea. Consider a standard
focal length f equal (by conventional definition of a standard lens)
to the diagonal of the image format; assume that the format is square to
simplify. The image size will be equal to 0.7f by 0.7f (diagonal size = 1.4
times the horizontal or vertical size of the square). If we assume that c=a/2=f/(2.N),
the number of equivalent image dots will be only 2× 0.7× N=1.4× N
both horizontally or vertically. Even at f/90, N=90 this yields a
total number of image points smaller than 20,000 (128 × 128)!!! Even if this
"un-sharp'' out-of-focus image concerns only a small fraction of the whole
image, such a terrible image quality is clearly unacceptable.
Now that we have shown that it is necessary to limit the upper value for
c
for image quality reasons, this upper limit being somewhat arbitrary, lets
us demonstrate that there is also an absolute, unquestionable, minimum value
for c due to diffraction effects.
This pure geometrical DOF approach is valid as long as diffraction effects
are neglected. Considering a value equal to N microns (1.22 × N
× l, with l = 0.8 µm
in the worst case) for a diffraction spot in the image plane, the other
reasonable condition is c(in microns) < N microns. For example
in medium 6x6cm format with c=50µm, f/32 is a reasonable f-stop
whereas f/64 is irrelevant to the present purely geometrical approach. In
4"x5" format taking c=150µm, f/128 will be the smallest
non-diffractive aperture for depth-of-field computations.
In macro work at 1:1 ratio (2f-2f), DOF does not depend on
the focal length
With all above-mentioned assumptions, equation (9) is
valid even for short distances p as in macro work, with p>f
of course to get a real image. This will be in fact irrelevant to our
purpose to find a simple expression and graphical interpretation for
far-distant objects, but is of practical use in macro- and
micro-photography. For example when p=2f at 1:1 magnification
ratio, the total depth of field is given by p2
- p1
= 4.N.c, and is totally independent from the focal length, a
well-know result.
A numerical computation in agreement with Stroebel's
diagrams
Unfortunately there is probably nothing really simple in terms of
understanding geometrically depth-of-field zones for close-up when
the film plane is tilted at a high angle with respect to the optical axis.
>From eq.(9) we easily derive a limit form valid for far
distant objects, i.e. p much greater than f i.e. p
» f. In this case we can write that f/p « 1 and 1-f/p
~ 1, Htrue= H+f
~ f . This yields the well-known expressions of eq.(2).
To go a little further, a numerical computation and graphical computer plot
(fig.7) is required. However it is interesting to
find the origin of the diagram presented in Stroebel's
excellent reference book [5], stating that
limit planes of acceptable sharpness intersect all in the same pivot
point Pf
located not in the lens plane (like in our approximate model here) but also
in the slanted object plane AS, and one focal length ahead
of the "regular'' Scheimpflug's pivot point S (figure 7).
Without any calculation when p decreases down to the limit value p=f,
it is easy to see from eq.(9) that both values p1
and p2 become equal to f this
defining the pivot point Pf.

Figure 7 : A better determination of
slanted object planes of acceptable sharpness, with a pivot point
located one focal length ahead of the lens, according to Stroebel (ref.[5])
and re-calculated numerically from eqs. (9)
From the computed diagram, here plotted the particular value
of c=f/1000 (c=f/1750 is mentioned sometimes and
is more stringent), the simplified approach of the "plus or minus H''
close-up lens (yielding slanted planes at large distances p) still
holds remarkably well at f/16, even in the macro range. However at f/64 in
the close-up range the exact calculation will be required, at least for
those inclined to the highest degree of precision, the approximate model
being still an excellent starting point to manually refine the focus for
slanted Scheimpflug's planes. This has been
computed with a very simple gnuplot [9]
freeware script, and will be gladly mailed to all interested readers.
2.1 Depth-of-Focus formulae
Starting from equation (7) defining depth-of-focus
limits without approximation, and combining with the exact DOF formulae (9)
and (10) yields a complicated expression
which would be useless except that its limit form when
H » f
is nothing but equation (8), the additional term
inside the bracket vanishing as f2/H2.
In most photographic situations, with a circle of confusion smaller than f/1000, the correcting factor is also of a magnitude smaller than
1/1000. Equation (11) is actually very close to
Descartes formula (8) connecting
p1
to p1' and p2
to p2', as long as the basic DOF
equation (1) is valid, namely when p » f a
common photographic situation except in macro work.
Equation (7) yields the expression for the
total
depth of focus p1' - p2'
equal to 2p' f/H. Subtituing H by its value
f2/(Nc) yields the expression
2Nc p'/f. In the case of the 1:1 magnification ratio
(2f-2f), p'=2f, the same value for depth-of-focus or
depth-of-field is found i.e. 4Nc, which makes sense considering the
perfect object-image symmetry at 1:1 ratio.
In the practical case of far distant objects,
p' will be very close
to one focal length f; in this case the total depth-of-focus is found
close to 2Nc. Surprisingly this result does not depend on the choice
of focal length f but only the conventional value for c. In
other words, for a given film format or a given camera (35mm, medium format,
large format) if the same circle of confusion is chosen for all lenses
covering a given format with the same camera body, the conclusion, under
those assumptions, is that the choice of focal length has no influence on
the total depth of focus for far distant objects.
However, in order to peacefully conclude on a potentially controversial
subject, the conventional value chosen for c increases somewhat
proportionally to the standard focal length when changing from 35 mm to
medium and large formats; in a sense it can also be said that depth-of-focus
is larger in large format than in small format. How this "large format
advantage'' actually helps getting better images in large format for given
mechanical manufacturing tolerances or film flatness cannot be simply
inferred without deeper investigations.
Acknowledgements
I am very grateful to Yves Colombe for his explanations about subtle pupil
effects in a non-symmetric or telecentric lens. In the more general case,
the projection of the exit pupil actually defines out-of-focus
"pseudo-images'' of object points. In the general case, those
"pseudo-images'' do not obey the classical depth-of-field formulae nor, of
course, basic object-to-true-image relations. Simon Clément has pointed to
me the fact the the "true'' hyperfocal distance becomes H+f
when the exact DOF formulae are in use. The subtle question of the
transversal magnification for out-of-focus pseudo-images has been clarified
by a passionate debate on one of the US Internet discussion groups on
photography, the key point being mentioned by Andrey Vorobyov [10].
Références
|
[1] |
Bob Wheeler, "Notes on
view camera'',
http://www.bobwheeler.com/photo/ViewCam.pdf |
|
[2] |
Martin Tai, "Scheimpflug
, Hinge and DOF'',
http://www.accessv.com/~martntai/
public_html/Leicafile/lfdof/tilt1.html |
|
[3] |
Harold M. Merklinger,
"View Camera Focus''
http://www.trenholm.org/hmmerk/VuCamTxt.pdf |
|
[4] |
Harold M. Merklinger,
http://www.trenholm.org/hmmerk/HMbooks5.html |
|
[5] |
Leslie D. Stroebel, "View
Camera Technique'', 7-th Ed., ISBN 0240803450, (Focal Press, 1999)
page 156 |
|
[6] |
Nicholas V. Sushkin,
"Depth of Field Calculation'',
http://www.dof.pcraft.com/dof.cgi |
|
[7] |
Henri Peyre's web site,
in French, "A Javascript to compute DOF limits'',
www.galerie-photo.com/profondeur_de_champ_calcul.html |
|
[8] |
Henri Peyre, "A
spreadsheet application to compute DOF'', in French,
www.galerie-photo.com/
profondeur_de_champ_avec_excel.html |
|
[9] |
"gnuplot, a freeware plotting program for many
computer platforms'',
http://www.ucc.ie/gnuplot/gnuplot.html,
http://sourceforge.net/projects/gnuplot |
|
[10] |
Discussion group on large format photography,
photo.net, july 2002 :
http://www.photo.net/bboard/q-and-a-fetch-msg?msg_id=003Rdn |
Emmanuel Bigler 16 novembre 2002
|