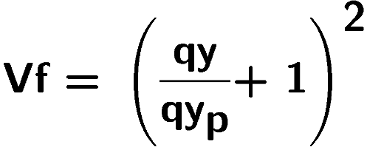[abonnement gratuit]

l'auteur

télécharger cet article
au format pdf

 
Les fondamentaux de l'optique
ISBN 978-2-212-13542-8, Eyrolles - mars 2013

Notes de lecture, « Les fondamentaux de l’optique »
de Jost J. Marchesi
(dans la série : les cours photo Eyrolles)

Traduit et adapté de l’allemand par Danielle Lafarge
avec la collaboration technique de Pascal Martin.

par Emmanuel Bigler

télécharger cet article au format pdf

Table des matières

• 1  Les lentilles tendraient-elles à disparaître ?

• 2  L’optique à la française serait-elle trop théorique ?

• 3  La force de l’édition Foto allemande

• 4  Les bases et les fondements

• 5  Vaste programme ! [17]

• 6  Une présentation claire et agréable

• 7  Les difficiles notions des éléments cardinaux des systèmes centrés

• 8  Le fameux facteur 1,22 a la vie dure

• 9  Technologie des verres, histoire et classification des objectifs

• 10  Le grand-formiste restera tout de même sur sa faim

• 11  Problèmes de traduction, de terminologie, textes ou figures discutables

• 12  Conclusion

1  Les lentilles tendraient-elles à disparaître ?

À une époque où c’est une gageure que de trouver (en dehors des reflex mono-objectif) un appareil photo numérique pour amateurs qui soit équipé d’un véritable viseur optique (et non pas d’un simple petit oculaire placé derrière un petit écran luminescent) la parution du livre de Jost Marchesi [2], « Les fondamentaux de l’optique » (ISBN 978-2-212-13542-8, Eyrolles - mars 2013) vient à point nommé pour nous rappeler que sans verres d’optique et sans lentilles, il n’y aurait de photographie qu’à l’aide d’un sténopé, et que même l’imagerie par sténopé obéit aux lois de l’optique physique et aux principes mathématiques des projections et des perspectives. C’est donc avec grand intérêt que nous avons lu et apprécié cet ouvrage traduit en français traitant d’un très vaste domaine d’application de l’optique à la photographie.

2  L’optique à la française serait-elle trop théorique ?

En France, si vous allez dans une librairie « scolaire et universitaire » pour y un chercher un livre d’optique, vous trouverez un très grand choix de livres destinés à l’enseignement en premier cycle universitaire et vous verrez un grand nombre de livres de cours et d’exercices corrigés pour les élèves des classes préparatoires aux concours des écoles d’ingénieur. L’optique n’est donc pas un parent pauvre de l’édition universitaire francophone, mais un rapide coup d’œil au contenu de ces ouvrages montrera au photographe amateur que ces livres ne sont pas faits pour lui, surtout les bouquins « de taupe » [3] dont la plupart ont comme objectif (sans jeu de mots) de faire réussir les élèves aux concours de façon qu’ils sachent résoudre le plus vite possible les grands classiques des exercices d’optique « académiques », c’est à dire ceux qu’on peut formuler de façon théorique en quelques lignes, qui n’ont qu’une seule solution, laquelle peut tenir sur plusieurs pages [4].

Au siècle dernier, les ouvrages photographiques de chez Paul Montel [5], par leur diversité et l’étendue des sujets traités, remplissaient fort bien leur mission didactique vis à vis des photographes amateurs et professionnels, mais on ne les trouve plus qu’en occasion ; et surtout : la « révolution numérique» étant passée par là, le doute s’est insinué dans l’esprit du lecteur du XXI^ème siècle, mettant en cause la pertinence des contenus de cette belle collection éditée au 189 de la rue Saint-Jacques à Paris. On ne peut que recommander au lecteur les différents ouvrages de René Bouillot, l’un des piliers de chez Paul Montel, et qui a remis à jour ses cours de photo chez VM et chez Dunod [6].

Chez Eyrolles, au siècle dernier, il y avait un livre d’optique de R. Taton [7] destiné principalement aux ingénieurs : « Bases de l’optique et principes des instruments » (Eyrolles, 1975) qui, après un exposé de l’optique géométrique dans la grande tradition française, passait en revue différents instruments utiles à l’ingénieur, par exemple : le théodolite. Autant dire que la pagination consacrée à l’appareil photo était très restreinte. Néanmoins ce n’est pas sans émotion qu’on trouvera en page 214 de cet ouvrage une photo du projecteur de diapositives 24x36 « ROB » qui fut le compagnon indispensable des belles soirées en famille à l’époque où la diapositive n’avait pas encore été chassée par le tirage sur papier d’après négatif couleur.

Il y a un excellent ouvrage d’optique géométrique du siècle dernier qui n’a pas pris une ride, du moins en ce qui concerne les principes, c’est le Moussa-Ponsonnet [8]. Certes, c’est franchement un bouquin pour le premier cycle universitaire et les taupins, mais on ne peut qu’en recommander chaudement la lecture à ceux qui veulent tout savoir sur les propriétés des lentilles minces et des systèmes optiques centrés, ainsi que les principes de base des instruments d’optique courants, appareils photo, loupes, jumelles, lunettes et télescopes, microscopes. Là encore, l’appareil photographique n’y est qu’effleuré, mais toutes les questions que se posent les photographes à propos des formules de conjugaison, de la profondeur de champ, la définition des pupilles, la photométrie et le pouvoir séparateur d’un objectif, sont traités simplement, avec un bagage mathématique requis qui ne dépasse pas celui de la classe de première scientifique des lycées (du moins, le programme des années 1960).

On pourrait bien entendu citer d’autres ouvrages plus récents, comme celui de Luc Dettwiller [9] ; pour un photographe, il restera probablement trop théorique et trop éloigné de la pratique de terrain. Mais il n’y a pas que des livres universitaires, il y a aussi des livres destinés à la formation professionnelle, comme le cours de Michel de Ferrières et Gérard Bouhot [11].

3  La force de l’édition Foto allemande

Certes, les traités universitaires anciens ne sont guère attrayants, ils manquent de belles images en couleurs. Arrivent donc aujourd’hui en version française « Les fondamentaux de l’optique » de Jost J. Marchesi, auteur bien connu pour de très nombreux ouvrages didactiques, dont une partie seulement avaient été traduits en français jusqu’à présent. Par exemple, on citera en allemand, de la fin du siècle dernier, une série complète en 3 volumes [13] chez l’éditeur Verlag Photographie qui a publié récemment (2011) une autre série destinée à l’auto-formation, Photokollegium [14]. C’est le tome 2 de cette série, Grundlagen des Optik in der Fotografie (ISBN 978-3-93131-62-1) qui est le Urtext de l’ouvrage en français dont nous parlons ici aujourd’hui. Si l’on mentionne que 550000 exemplaires du « Photokollegium » ont été vendus depuis 2011 [15], on mesurera ce que peut représenter la force de l’édition en langue allemande dans le domaine de la Foto : elle est simplement à la mesure de la force du marché de la photographie dans l’ensemble des pays germanophones.

Signalons que les tomes 1 (photographie argentique) et 3 (prise de vue) du Photokollegium sont en préparation pour le cours photo Eyrolles (annonce faite en page 2 de l’ouvrage analysé ici).

4  Les bases et les fondements

Il en va des fondamentaux comme des spaghetti ou des Eurockéennes® de Belfort® : cela n’existe qu’au pluriel. Un rapide coup d’œil à un dictionnaire d’allemand nous explique que les Grundlagen sont les bases, comme dans le bouquin de R. Taton [7], ou bien les fondements. Certes, ce dernier mot était l’objet de bien mauvaises plaisanteries chez les potaches des années 1920-1930 (lorsque le cours de physique des lycées français était essentiellement consacré à l’optique géométrique), d’autant plus que les fondements sont souvent philosophiques comme les Fondements de la métaphysique des mœurs de Kant (Grundlegung zur Metaphysik der Sitten). Et pourtant, le récent livre d’optique de référence de J.P. Perez s’appelle bel et bien : « Optique, fondements et applications » [19]. Mais qu’à cela ne tienne, il semblerait que les scientifiques francophones préfèrent finalement les bases, comme ces Bases du calcul des structures si utiles aux ingénieurs. Et les fondamentaux, me direz-vous ? Eh bien, en l’an 2013, ils n’ont pas encore trouvé leur place dans le Le Trésor de la Langue Française Informatisé [16], qui ne leur accorde qu’un modeste statut d’adjectif, pas encore celui de substantif ; mais cela ne saurait tarder, depuis le temps que les bons conseilleurs nous incitent à revenir aux fondamentaux, ce n’est qu’une affaire de quelques mois ; René Bouillot lui-même, il y a déjà plus de 10 ans, nous proposait déjà ses « fondamentaux argentiques » [6].

5  Vaste programme ! [17]

L’ouvrage de J. Marchesi est organisé en 41 leçons, dont on pourrait d’ailleurs se demander si chacune pourrait correspondre à une période de 45 minutes, l’unité de base de l’enseignement en Suisse. Les notions abordées se rattachent à l’optique géométrique et aux instruments d’optique, à l’optique physique (lumière, couleur, photométrie, interférences, diffraction, polarisation), à la technologie des verres d’optique, et traite de notions spécifiques à la photographie que sont, entre autres exemples, les principaux types d’objectifs photographiques et leur histoire, la profondeur de champ, les facteurs de soufflet (appelés : Facteurs d’allongement du tirage) et la Règle de Scheimpflug. Quand on aura rappelé que le Moussa-Ponsonnet [8] qui traite essentiellement d’optique géométrique, et ne fait qu’aborder succinctement les principes des instruments, comprend 475 pages ; et que la « bible » francophone de l’optique physique, le Bruhat revu par Kastler [18] en compte plus de mille dans les toutes dernières éditions ; et qu’un ouvrage de référence, plus récent, le Perez [19] en comporte 700, on comprendra le défi formidable à relever qui consiste à faire passer un minimum de toutes ces notions à destination des photographes en auto-formation, sans dépasser les 128 pages d’un ouvrage de prix abordable.

6  Une présentation claire et agréable

Pour un ouvrage d’auto-formation, la présentation, la typographie, les figures se doivent d’être extrêmement attractives. Sur ces points, l’ouvrage est une réussite, et on ne boude pas son plaisir à voir sortir une photo d’excursion dans la région du glacier d’Aletsch pour nous rappeler les joies de la photo de paysage au milieu d’une nature qui illustre traditionnellement les calendriers suisses. Si la comparaison avec les traités universitaires français du siècle dernier se passe de tout commentaire, il faut rappeler que la collection d’ouvrages didactiques de chez Paul Montel était, elle aussi, très bien présentée et très bien illustrée. On pourra également mentionner au passage que les livres de mathématiques et de physique des classes secondaires françaises sont, eux aussi, devenus aujourd’hui très attractifs ; en particulier, les livres de physique de niveau lycée où l’on parle d’optique n’ont plus rien à voir avec ce qui fut autrefois le pain quotidien fort rébarbatif des potaches.

Le lecteur est incité à résoudre des exercices, énoncés en marge du texte, qui sont souvent des expérimentations personnelles, comme étudier la double réflexion dans son miroir de salle de bain ; donc rien à voir avec l’exercice académique « taupinal », bien entendu. Pour autant, les formules ne sont pas absentes, et l’ouvrage peut aussi être lu comme un aide-mémoire d’optique géométrique théorique, toutes les formules utiles au photographe sont là, depuis les formules de conjugaison des lentilles minces et des systèmes centrés, jusqu’aux classiques formules de profondeur de champ, et même sans oublier les terribles formules donnant le facteur de soufflet pour une optique dissymétrique inversée !

On regrettera néanmoins que les figures, bien qu’elles soient toutes légendées, ne soient pas numérotées.

7  Les difficiles notions des éléments cardinaux des systèmes centrés

L’ouvrage suit la progression classique, en partant du sténopé, puis traite de la lentille mince, puis de la lentille épaisse et enfin du système épais.

En page 13, donc très tôt dans l’ouvrage, on explique clairement, photos à l’appui, que la distance focale est sans effet sur le rendu de la perspective dans l’image photographique. Ce qui ne peut que nous réjouir, mais on n’explique pas pourquoi cela reste vrai avec une optique épaisse de formule compliquée, puisqu’en page 13 de l’ouvrage, on sort à peine du sténopé ! Le fait que le tracé de rayons du sténopé puisse rester valable dans presque tous les cas avec une optique photographique fait partie de ces questions parfois posées sur les forums, mais pour lesquelles une réponse détaillée ne s’écrit pas en trois lignes [20].

On pourrait se demander si cette démarche classique a encore un sens aujourd’hui, c’est à dire de partir de l’élément de base, le dioptre ou le miroir plan ou sphérique, puis la lentille mince, pour arriver à la description qualitative des très complexes zooms à usage photographique.
Dans l’enseignement de l’électronique, si les étudiants ne sont pas des électroniciens spécialisés, on est obligé aujourd’hui de faire l’impasse sur le transistor, cette brique de base de l’électronique des semi-conducteurs. Demandez à un enfant né en l’an 2000 s’il a déjà vu un transistor, la probabilité est très élevée pour qu’il ne sache absolument pas ce que c’est ; et si vous voulez lui en montrer un, vous serez à la peine pour en dénicher un dans vos appareils domestiques, à l’exception, peut-être, du gros transistor de puissance en forme de losange qui est vissé sur son radiateur à ailettes striées noires à l’arrière d’un amplificateur de puissance audio.

Rien de tel avec la lentille mince, qui est présente dans la vie quotidienne sous forme de verre de lunettes (le chapitre du livre traitant de la vision humaine est remarquablement bien fait), ou sous forme de loupe ; la formation de l’image d’une fenêtre, sur sa main, vue à travers une simple loupe, reste une expérience merveilleuse. Plus difficile sera d’expliquer aux enfants pourquoi le verre de lunette de myope ne donne pas la même chose que la loupe !

Dans un processeur de micro-ordinateur, les transistors se comptent par millions ; dans un zoom ciné professionnel, avec 20 lentilles on est déjà au bout du monde. Donc la comparaison de la lentille et du transistor est sans objet.

Malgré son utilité pédagogique indéniable, il n’y a probablement pas de système optique plus décevant qu’une simple lentille mince convergente pour celui qui veut se fabriquer un appareil photographique ; même le sténopé, avec son ultra grand angle de champ et son absence de distorsion, est moins décevant. Pour bien moins cher qu’une lentille pour montages d’enseignement dans sa monture et sur son pied, on peut avoir à volonté un choix extraordinaire d’objectifs photographiques de prise de vue, de projection ou de banc de reproduction en occasion, qui donneront des images presque parfaites.

Dans le livre de J. Marchesi, le passage de la lentille mince au système épais est probablement trop rapide, la notion de plans principaux est certainement l’une des plus délicates qui soient [21]. Dessiner des lentilles épaisses avec la position des points principaux H et H’ (la notation consacrée H venant de l’allemand : Hauptpunkt, Hauptebene) comme dans tous les bouquins universitaires classiques n’a aucun intérêt photographique, mais dans un cours de base, la lentille épaisse reste probablement un passage obligé entre le modèle de la lentille mince et le système complexe de l’objectif photographique « moderne », pour reprendre le titre de l’une des leçons du livre.

8  Le fameux facteur 1,22 a la vie dure

Parmi les notions d’optique physique abordées, la leçon N° 22 relative à la polarisation est très claire et rassemble en quelques pages bien articulées ce que le photographe doit savoir dans l’utilisation des filtres polarisants.

L’autre gros morceau de l’optique physique, la diffraction, est présentée dans la leçon N° 20 de la façon traditionnelle, à partir de l’estimation de la largeur à mi-hauteur d’une tache de diffraction de Fraunhofer formée par un instrument à pupille circulaire. Depuis la fin du XIX^ème siècle, on pourrait penser qu’il n’y a pas d’autre façon de présenter l’effet de la diffraction sur le pouvoir de résolution d’un spectrographe ou d’un spectromètre, et le pouvoir séparateur d’un télescope ou d’un appareil photo. Cette présentation est également celle du cours classique de Moussa-Ponsonnet [8], qui donne les formules sans démonstration, mais assorties d’une excellente discussion sur le pouvoir séparateur lorsque la diffraction est le facteur qui limite, à laquelle il semble difficile d’ajouter quoi que ce soit même aujourd’hui.

Cette manière de présenter nous prouve que la déférence envers Lord Rayleigh et son célèbre critère, associée à l’indéboulonnable facteur 1,22 de la tache de diffraction de largeur 1,22 Nλ induite par une pupille parfaitement circulaire, réussissent à défier le temps malgré les progrès de l’optique. Ces progrès ne datent pas d’hier puisque dès 1946 dans « L’intégrale de Fourier et ses applications à l’optique » [22], P.M. Duffieux propose une autre façon de voir les choses bien plus proche des préoccupations du XXI^ème siècle relatives la détection des images par un capteur numérique avec échantillonnage spatial périodique. Dans cette approche, qui est celle de l’optique de Fourier, on considère le système optique comme un filtre des fréquences spatiales capable de passer toutes les paires de lignes de l’objet, jusqu’à une certaine valeur limite qui est imposée de façon absolue par la diffraction. Il se trouve que la plus petite période, mesurée dans l’image, capable de passer à travers un objectif de nombre d’ouverture N, c’est Nλ où λ est la longueur d’onde, dans notre cas, le visible entre 0,4 et 0,7 micron (limite de la sensibilité effective de l’œil humain, bien que la définition classique du spectre visible s’étende jusqu’à 0,8 micron). Plus besoin de ce facteur 1,22 [23] qui n’a aucun sens. D’abord, la pupille n’est jamais parfaitement circulaire, les adorateurs du Synchro Compur l’aiment pentagonale, les zélateurs du Copal la préfèrent heptagonale. À supposer que la pupille soit vraiment parfaitement circulaire, la précision du 1,22 à deux chiffres après la virgule est en elle-même une franche rigolade qui dure depuis au moins cent vingt ans ; écoutons ce que Lord Rayleigh lui-même en disait :

Cette règle est pratique du fait de sa simplicité, et elle est suffisamment précise en comparaison de l’incertitude colport�������������������������e par le terme de résolution [24].

En utilisant la p����������������������riode de coupure de diffraction, non seulement le terme Nλ est parfaitement exact pour cette période de coupure sans approximation aucune et sans discussion possible, mais en plus on fait l’économie de se demander pourquoi 1,22 et non pas 1,1 ou 1,57. Si on couple cette notion de période de coupure avec la période de la grille de pixels nécessaires à échantillonner une image analogique sans « pertes de paires de ligne » avec un capteur silicium, à 2 points par période suivant le théorème d’échantillonnage [25], on arrive à une estimation du nombre maximal de pixels effectivement résolus derrière une optique parfaite qui s’écrit en trois lignes de calcul [26]. Certes, pour la formule p = Nλ qui s’écrit en quatre caractères dont une lettre grecque, le nombre de pages de mathématiques et de physique qu’il faudrait avoir lues pour tout expliquer dans l’ultra-détail est proprement vertigineux ... alors, pour une fois, on utilisera avec gourmandise l’argument-massue de ceux qui préfèrent ne pas savoir le détail des principes optiques qui rendent possible leur activité photographique : « Seul le résultat compte ! »

9  Technologie des verres, histoire et classification des objectifs

La leçon N°23 concernant la technologie des verres d’optique est fort bien venue. Il est rare de trouver un paragraphe à ce sujet dans les bouquins français de photo du siècle dernier.

Les leçons 35 à 39 passent en revue l’histoire des objectifs, leur classification et leurs propriétés, développements classiques dans la plupart des bouquins traitant des moyens et grands formats, mais très bien illustrée ici par Jost Marchesi.

Dans ces leçons, l’industrie allemande se taille la part du lion et rappelle douloureusement que l’industrie optique française, à l’exception remarquable des verres ophtalmiques, est devenue littéralement invisible du grand public, ce qui ne veut pas dire, loin de là, qu’elle n’existe plus. Si l’euro-patriote ne peut que se réjouir de voir mis en exergue le rôle éminent joué par les savants et les industriels européens au sens large dans les leçons indiquées, le franchouillard hexagonal protestera à juste titre que dans le bouquin, la firme Angénieux (dont certains objectifs sont encore sur la Lune à côté des Zeiss de la NASA depuis 1969 [27]), n’est mentionnée que pour être créditée de l’invention du mot « zoom » (sans mentionner que le terme « rétrofocus » doit être aussi crédité à la même entreprise française), et que l’un des premiers zooms pour le cinéma est le Pan-Cinor de Roger Cuvillier chez SOM-Berthiot en 1950 [28].

10  Le grand-formiste restera tout de même sur sa faim

Et le grand-formiste dans tout ça ? Il appréciera de voir expliquée en détail la notion de cercle d’image ; lire l’histoire et la classification des optiques depuis le Petzval lui sera agréable et instructif s’il n’a pas déjà lu le Kingslake [29]. Il aura plaisir à voir une belle photo d’un Imagon de chez Rodenstock (avec un exemple d’image vaporeuse à souhait, page 89, mais on sort juste du chapitre sur l’aberration de sphéricité, l’illustration est donc parfaite). Il savourera en connaisseur l’encadré de la page 106 décrivant l’Hypergon de chez Goerz avec son petit ventilateur frontal destiné à combattre l’effroyable loi photométrique en cos⁴(θ). Mais concernant la chambre et ses mouvements, outre que l’offre actuelle de chambres semble, d’après les photos du bouquin, se limiter à une seule marque zürichoise, il s’étonnera de ce que les mouvements et toutes les particularités de la prise de vue en grand format ne soient traités qu’en 5 pages seulement. Mais sans doute la chambre ne fait-elle plus partie des fondamentaux de la photographie ? Affaire à suivre dans les autres volumes du Photokollegium à paraître en version française, en particulier ceux qui traiteront de la prise de vue ; mais en attendant et en langue française, autant lire le Bouillot [30], le Groulx [31], ou bien en anglais : le Stroebel [32], le Shaman [33] (qui ne traite pratiquement que des mouvements !) sans oublier, bien entendu, Saint Ansel [34].

11  Problèmes de traduction, de terminologie, textes ou figures discutables

L’ampleur de la tâche consistant à réunir toutes ces notions d’optique en 125 pages, en vue d’une auto-formation de lecteurs a priori peu versés en physique générale, conduit nécessairement, une fois ou l’autre, à des raccourcis contestables. De plus, ceux qui n’ont jamais eu à traduire de textes techniques mesurent mal la difficulté particulière de ce travail, et ne soupçonnent pas la capacité diabolique que peuvent avoir les coquilles de détail à échapper à l’attention du correcteur professionnel le mieux aguerri.

En page 31, l’encadré à propos de la diminution de l’éclairement d’un faisceau divergent propose le rayon laser comme exemple de faisceau parfaitement parallèle pour lequel l’intensité ne diminuerait pas au cours de la propagation. Les astrophysiciens qui mesurent la distance Terre-Lune par un tir laser sur l’un des réflecteurs déposés par les missions lunaires du siècle dernier aimeraient bien qu’il en soit ainsi ; un faisceau laser n’échappe pas, hélas, à la loi de décroissance en 1/r², même si sa divergence est extraordinairement faible, de l’ordre de la minute d’arc pour un laser émettant dans le visible, dont le faisceau est de 1 mm de diamètre en sortie de la source.

Page 75, l’interstice n’est pas défini comme on le fait habituellement dans les traités d’optique géométrique français où le terme d’interstice est souvent utilisé pour désigner l’écart HH’ = NN’ entre plans principaux d’un système optique utilisé dans l’air (voir par exemple la référence [12]), ou bien encore pour désigner l’écart entre les plans principaux de deux systèmes optiques associés l’un derrière l’autre. La définition d’interstice donnée en page 75 du livre de J. Marchesi est la distance entre l’objet et le sommet de la première lentille, ou bien la distance entre le sommet de la dernière lentille et l’image. Mais la figure en haut de la page 75 semble définir l’interstice différemment du texte, avec le symbole "d" qui est, à lire sur la figure, l’écart entre les sommets d’une lentille épaisse. Il y a probablement quelque chose qui ne va pas dans la figure. La notion d’interstice est à nouveau évoquée en page 110 à propos du principe des objectifs rétrofocus ; le terme d’interstice y est utilisé conformément à sa définition textuelle de la page 75, pour désigner une notion qu’on appellerait habituellement tirage optique (distance entre la dernière lentille et le foyer). Cela ne porte guère à conséquence, tous les termes ne sont pas forcément normalisés, mais il est dommage que les figures ne soient pas numérotées, car il est difficile de définir une notion telle qu’un interstice optique sans renvoyer à une figure claire et facile à repérer par son numéro.

Page 86, prendre le rayon moyen passant par le centre d’une lentille mince pour expliquer l’origine de l’aberration chromatique transversale est une mauvaise idée, puisque les rayons ne sont pas déviés, quelle que soit leur couleur, à la traversée du centre d’une lentille mince convergente. Certes, dans une lentille épaisse, il y aura un tout petit déplacement latéral de ce rayon moyen, qui va dépendre de la longueur d’onde et de l’épaisseur de verre traversée, mais une tentative d’explication du chromatisme transversal demande : soit un tracé de rayon à travers une lentille mince mais sans passer par le centre, soit un tracé de rayon idéal pour un système épais dont les pupilles ne sont pas placées aux plans principaux.

Ce qui est étonnant, ce serait plutôt le grand nombre d’exemples des bases de l’optique photographique qu’on peut traiter avec une lentille mince diaphragmée en son centre (rendu de perspective, formules de conjugaison, photométrie et réglage du diaphragme, profondeur de champ) mais il faut bien un jour ou l’autre que le modèle tombe en défaut ; l’explication du chromatisme transversal est justement l’un des cas où il ne faut surtout pas aller chercher une lentille mince diaphragmée en son centre.

Écrit probablement en 2010, le livre de J. Marchesi nous explique en bas de la page 100 : « Pour ne pas dépasser la limite inférieure de la taille de pixels critique, les capteurs plein format [donc format 24x36 mm] ne doivent pas comporter plus de 20 mégapixels ». Voir le petit calcul [26] en fin de cet article qui montre que la limite théorique absolue imposée par la diffraction derrière une optique parfaite ouvrant à f/8 serait, dans sa limite théorique ultime, de l’ordre de 110 mégapixels. En attendant, les heureux possesseurs d’un reflex 24x36 avec un capteur de 36 mégapixels apprécieront également cette recommandation.

En dehors de ces quelques remarques très techniques, il reste très peu de d’éléments qui n’ont pas été traduits, soit intentionnellement, soit parce que leur côté microscopique a échappé à la vigilance des correcteurs. C’est donc un plaisir délicieux et parfaitement inutile que de passer au peigne fin le texte et les figures pour en détecter les coquilles.

À partir de la page 44 est introduite la notion de grandissement transversal, pour lequel la très contestable notation qy est employée, puisqu’il peut y avoir confusion avec le produit des deux variables q et y. Du coup cela oblige l’auteur à rajouter un point entre symboles littéraux pour désigner une multiplication, par exemple en page 44 on peut lire : x’ = qy • x une notation qui n’est pas recommandée en typographie scientifique française mais qu’on peut comprendre.

On peut imaginer que toutes les équations étant hors texte, elles ont été importées directement sans traduction ni adaptation ; re-saisir toutes les formules est une tâche longue et coûteuse. Dans les ouvrages français, le grandissement transversal est très souvent nommé γ, c’est le cas chez Eyrolles pour le bouquin de R. Taton [7] (mais c’était en 1975). Impossible hélas, car il y a conflit avec l’usage du symbole γ, qui apparaît en page 82 et désigne l’angle de champ total couvert par une optique de chambre, une notation consacrée en terminologie allemande, dans laquelle on désigne par ω ou bien encore w l’angle correspondant à la diagonale du format (donc plus petite que γ).

Pour le grandissement transversal, la notation g_y est également consacrée dans les ouvrages français, pour la mettre en parallèle avec le grossissement angulaire g_α ; sans savoir d’où vient le symbole q, on aurait cependant bien compris une notation dans le genre q_y, avec le y en indice inférieur. Mais cela aurait conduit à un empilement digne de la célèbre affiche publicitaire des Frères Ripolin lorsqu’il s’agit de définir le grandissement pupillaire, qui aurait alors dû être noté : q_yp. Cette notion est introduite en page 81 sous la notation qy_p. Avec un facteur de soufflet défini de la même façon ambiguë comme Vf, qui pourait être le produit d’une vitesse V par la focale f, (Vf provient en fait du Verlängerungsfaktor [35]) on espère que les lecteurs qui auront effectivement l’usage du facteur de soufflet s’y retrouveront lorsqu’ils devront déchiffrer la formule :

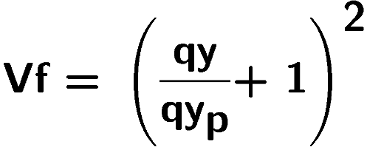
Concernant l’origine mystérieuse de ce qy, on en est finalement r��������������������������������duit aux conjectures, puisqu��une rapide recherche ne nous fournit comme piste qu’une Abbildungsmaßstab [36], symbolisée par la lettre grecque beta, notation famili�����re pour eux qui connaissent les docs techniques allemandes des objectifs de chambre, où les courbes FTM sont toujours spécifiées pour un grandissement donné, noté β′.

Page 69, dans la leçon N°23 sur les verres d’optique, on apprécie de voir la fiche technique du fameux verre Schott BK7, mais ceux qui ne lisent pas l’allemand seront à la peine pour comprendre ce qui n’est qu’un coupez-collez de la fiche allemande. On espère que l’honorable firme de Mayence, qui a des clients dans tous les pays, ne se contente pas de la fiche technique en allemand lorsqu’elle vend ses produits à l’autre bout du monde.

Page 81 en bas à droite, dans l’exercice, les AP et EP non traduits de l’allemand nous rappellent ce que sont l’AustrittsPupille [37] et l’EinstrittsPupille [38] dans une optique dissymétrique de grandissement pupillaire différent de l’unité.

Page 83, à propos du diamètre du cercle-image, le lecteur voit débarquer dans une formule un d_BK dont il va peut-être se demander le lien avec le verre BK7 cité précédemment ; aucun rapport évidemment, il ne s’agit que du BildKreis [39]. Quant au symbole d, chacun aura compris qu’il s’agit d’un Durchmesser, et certainement pas un diamètre.

Page 98 et suivantes, on nous parle de MTF pour la Fonction de Transfert de Modulation, c’est effectivement l’abréviation anglaise. En hochdeutsch, on dit : Modulationsübertragungsfunktion, Modulationsübertragungsfaktor ou bien encore Kontrastübertragungsfunktion, on s’attendait donc à voir des KUF ou des MUF aux belles courbes apparaître à côté du d_BK. Mais l’allemand technique est très perméable aux anglicismes, on dit donc aussi, en mélangeant un peu tout : Modulationstransferfunktion [40]. En français on dira : FTM, tout simplement.

Et enfin en page 116, le lecteur se demandera ce qu’est cette patatoïde bleue qui empêche de placer la chambre directement en face de l’édifice à photographier, le mystérieux Teich n’est autre qu’un étang mal placé mais fort utile pour faire sentir la nécessité d’un décentrement latéral.

12  Conclusion

En refermant le livre, on ne doute pas qu’il trouvera son lectorat francophone, vu le succès de la série originale Photokollegium en allemand. L’ouvrage n’intéressera probablement pas l’amateur de moyens et grands formats, en particulier la partie spécifique aux mouvements de la chambre est bien trop restreinte. Mais sans doute, pour un lecteur lassé de prendre des photos avec un appareil auto-tout numérique (cette dernière catégorie d’appareils photo ayant, finalement, simplement poussé à peine plus loin la facilité extrême d’utilisation qui était déjà de mise avec les appareils auto-tout à film), l’ouvrage « Les fondamentaux de l’optique » de Jost Marchesi donnera envie d’en savoir plus ; la découverte de ce qu’est un Hypergon, l’œil de chat dans un planar 1,4 de 50, les images vaporeuses de l’Imagon, et la curiosité de comprendre et de comparer les diagrammes FTM des optiques « de course », l’incitera à aller plus loin dans ses lectures. Il regrettera probablement de ne pas trouver de bibliographie dans le livre, à part l’annonce des prochains volumes de la série, et quelques pointeurs vers des sites Internet, dans le corps du texte ; mais, ami lecteur qui nous lisez ici sur www.galerie-photo.com, vous savez où vous adresser, et si la bibliographie juste ci-dessous ne vous satisfait pas, il vous suffira de poser toutes les questions restées sans réponse sur notre forum http://www.galerie-photo.info.

Bibliographie, Notes & Références

télécharger cet article au format pdf

 
Les fondamentaux de l'optique
ISBN 978-2-212-13542-8, Eyrolles - mars 2013

Dernière mise à jour : 2013