[abonnement gratuit]

l'auteur

  Télécharger l'article
au format pdf
 

par Emmanuel BIGLER

ENSMM
26 chemin de l'Épitaphe
F-25030 Besançon cedex
mél : Mail.

Résumé : Après avoir examiné les questions de résolution et d'échantillonnage pour les images sur film et les images obtenues par capture directe sur silicium, nous poursuivons notre comparaison entre les deux types de détecteurs photographiques sur le plan des effets de granularité (film) et de bruit. Le but ici n'est pas de présenter un modèle complet mais de mettre en place quelques notions simples comme celles du bruit de photons et de l'équivalence entre le bruit de granularité du film et le bruit d'un détecteur de photons affecté d'une faible efficacité de détection. La comparaison avec les détecteurs d'image silicium est donc facilitée, ces derniers étant des capteurs électroniques pour lesquels on a mis au point des méthodes de caractérisation assez simples des performances en termes de bruit.

Introduction

Tout photographe sait ce qu'est le grain du film, la présence de cette texture aléatoire plus ou moins fine qui se superpose à l'image analogique est une donnée première de la photographie traditionnelle. Si on connaît assez bien les compromis entre la finesse de grain et la sensibilité du film, ainsi que l'effet de différents révélateurs sur l'acutance (en bord de trait) et l'importance de la granularité, peut-être les photographes sont-ils moins habitués à raisonner en termes d'efficacité de détection et de rapport signal sur bruit. Ce sont plutôt les astrophysiciens, poussant les films à leurs limites, qui avaient creusé ces notions ; on les trouve néanmoins expliquées dans le traité magistral de Pierre Glafkidès destiné à tous les photographes, ouvrage rédigé dans les années 1960-1970 [1].

Clairement les notions de signal et de bruit sont communes à l'électronique et à l'imagerie, elles sont rassemblées dans le champ scientifique et technique du traitement du signal et des images, elles ont été développées au départ pour les applications scientifiques civiles et militaires.

Prenons l'exemple typique de la détection de systèmes d'armes ennemis par des prises de vue aériennes. La première idée qui vient à l'esprit est celle de résolution, on veut pouvoir discerner quel modèle de fusil le fantassin adverse possède, lire éventuellement le numéro de série sur les jumelles des observateurs de l'autre bord. Pour cela, encore faut-il que l'image ne soit pas noyée dans le bruit.

Les contribuables qui ont donc soutenu par leur impôt les recherches civiles et militaires en matière de détection d'images électroniques de haute performance dans la deuxième moitié du XXème siècle sont donc en droit d'attendre en ce début de XXIème siècle un retour vers leur usage personnel de tout cet investissement. On peut donc dire très sérieusement que l'imagerie électronique numérique à la portée des photographes professionnels et amateurs est une conséquence lointaine des investissements du passé, comme les progrès en optique et films au départ réservés aux usages militaires ou scientifiques sont désormais à la portée de tous. Il faut donc s'en réjouir, c'est dans cet esprit que nous proposons d'examiner ici le gain très remarquable en termes de bruit qu'apporte la détection directe d'images par les capteurs silicium.

Il faut aussi tenir compte du bruit !

Nous avons vu dans la première partie de cet article [2] que si on tient compte du rapport d'agrandissement moindre requis par le plan film de grand format, on s'aperçoit qu'en termes de FTM, donc de résolution, le film, à condition d'être agrandi, pour fixer les idées, 4 fois moins que l'image numérique, l'emporte clairement. Sous ces conditions, comment se fait-il que les résultats observés visuellement [3] ne confirment pas totalement cet avantage ?

Nous nous hasarderons ici à proposer une piste pour tenter d'expliquer ce paradoxe apparent, qu'on peut résumer ainsi : il suffit d'assez peu de pixels par détection directe avec un capteur, si on compare avec la surface de film nécessaire à obtenir la même qualité. Jusqu'à présent, nous n'avons considéré que des détecteurs sans bruit propre, or dans l'appréciation de la qualité d'une image, la présence de bruit joue un rôle important.

Pour le film, le bruit nous est familier, c'est le grain, ou bruit de granularité. Lorsqu'on agrandit l'image directement à travers une optique, on ne fait pas qu'un simple agrandissement du motif de grain, les choses sont nettement plus complexes. On connaît l'effet Callier qui modifie les densités moyennes apparentes sous l'agrandisseur en fonction du type d'éclairage (dirigé, semi-dirigé, diffus) et de l'effet diffusant du film, mais il existe un effet Callier « généralisé » qui relie les fluctuations de densité du film aux fluctuations de densité dans l'image. Cet effet n'a été reconnu et modélisé que dans les dernières années où les chercheurs travaillaient encore sur les images analogiques, la théorie en est très difficile [4].

Plus simplement, on peut considérer l'exemple de l'image agrandie d'un ciel. Lorsqu'on agrandit optiquement une telle image d'après un film, on finit toujours par apercevoir un effet de grain ; alors que s'il s'agit d'un tirage fait d'après numérisation, aucun grain n'apparaît. Ceci tout simplement parce qu'un ciel est une portion de l'image qui ne contient en général pas de très fins détails, aucune « petite grille fine » susceptible de donner un effet de moiré, son interpolation s'effectue donc sans limite d'agrandissement, de façon parfaite à travers les chaînes graphiques numériques actuelles. Oublions les pauvres images « pixellisées » d'il y a quelques années, non, l'image numérique ce n'est pas juxtaposer simplement des petits carrés de couleur sans aucun lien entre eux !

Certes, si on fait une prise de vue numérique directe en réglant la sensibilité ISO équivalente de l'appareil sur une valeur très élevée, donc avec un temps de pose court et très peu de photons détectés, il finit par apparaître un bruit propre au détecteur, mais ce niveau de bruit est en pratique incomparablement plus faible que celui du film.

Le film a une structure granulaire et une faible efficacité de détection !

En quelques mots, on peut dire que la supériorité du capteur silicium sur le film tient dans son absence de structure granulaire et dans sa meilleure efficacité quantique de détection. Dans un détecteur parfait qui serait dépourvu de structure granulaire aléatoire et dépourvu de bruit propre, il resterait néanmoins une limitation à la qualité des images, imposée de façon ultime par les fluctuations naturelles du nombre de photons incidents par pixel. Un détecteur hypothétique sans bruit propre mais qui « oublie » de compter un certain nombre de photons incidents, par exemple qui n'en compterait que 1%, est qualifié d'un rendement quantique de 1%. C'est le cas du film ; bien entendu le film n'est pas un compteur de photons, mais une analyse reliant le bruit de granularité aux fluctuations naturelles du nombre de photons en entrée conduit à affecter un rendement quantique équivalent qui, pour le film, ne dépasse guère quelques pourcents dans les meilleurs cas. Pour les détecteurs d'images silicium à l'usage de la photographie professionnelle, on est déjà à 20% de rendement quantique [10].

Les deux points-clés de la discussion sont que le film non seulement a un rendement quantique inférieur, d'où un bruit lié au signal à sensibilité égale qui est très désavantageux par rapport à celui d'un capteur, mais de plus, le film présente une structure granulaire propre qu'on ne peut pas effacer par interpolation.

Tentative de comparaison entre un film et un capteur en termes de bruit

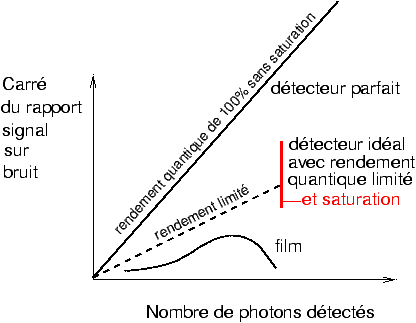
Figure 1: Comparaison de l'évolution du rapport signal sur bruit entre un détecteur parfait, un détecteur idéal à rendement limité et un film (d'après P. Glafkidès [5])

Un capteur silicium se comporte presque comme un capteur idéal à rendement limité avec saturation lorsque le nombre d'électrons maximal par pixel est atteint. En réalité aux très faibles nombres de photons le capteur laisse apparaître un bruit propre non représenté sur la figure. Le film considéré comme détecteur de photons a non seulement un rendement quantique équivalent plus faible que les capteurs silicium, mais de plus il faut poser juste pour que le meilleur rendement soit atteint. Certes, ce problème de rapport signal sur bruit ne se pose de façon aiguë que pour la photographie d'objets très peu lumineux comme en astrophotographie, mais on voit bien une limite très fondamentale apparaître.

Essayons, juste pour fixer un ordre de grandeur, et sans trop de rigueur, de comparer le bruit de granularité d'un très bon film moderne avec le bruit du capteur utilisé dans le Canon EOS 5D. On lira dans l'annexe 3 les détails de cette comparaison qui s'appuie sur une série d'articles de Christian Buil [6].

On peut montrer que dans les conditions photographiques usuelles o�� on n'est ni à très faible flux comme en astrophotographie, ni à saturation (ce qui suppose de mesurer l'étendue des luminances de son sujet pour ne pas « griller les blancs »), l'influence du bruit propre du détecteur devient négligeable, seul subsiste un bruit lié aux fluctuations naturelles du nombre d'électrons détectés, c'est à dire un bruit déterminé par le nombre de photons reçus par le pixel pendant la pose et le rendement quantique de détection du capteur. C'est ce que constate Christian Buil dans son analyse serrée du bruit des capteurs équipant les appareils reflex numériques [6].

Une estimation comparative du bruit du capteur de l'EOS 5D réglé sur 400 ISO et du bruit de granularité de la Provia 100F autour de la densité unité nous montre que l'EOS 5D est au moins deux fois meilleur en bruit. On pourrait imaginer bien entendu utiliser le capteur avec une sensibilité équivalente de 100 ISO ou plus bas ; le problème avec l'utilisation des capteurs avec un réglage de sensibilité ISO trop basse, donc avec une surexposition, c'est qu'on arrive très facilement à la saturation, Henri Gaud dans ses articles sur la sensitométrie du numérique [7] montre qu'en pratique il vaut toujours mieux sous-exposer que surexposer, on a donc un comportement qui rappelle un peu celui des diapositives (couleurs ou noir et blanc, peu importe) pour lesquelles la surexposition est toujours catastrophique. Mais s'il est possible sans saturer l'image de régler la sensibilité à 100 ISO plutôt que 400, c'est à dire admettre 4 fois plus de photons, le gain théorique en rapport signal sur bruit sera un facteur 2 supplémentaire, donc un facteur 4 au total par rapport à un excellent film de même sensibilité.

On pourrait objecter que les capteurs dépourvus de micro-lentilles, comme ceux nécessaires à l'utilisation en architecture avec bascules et décentrements, avec des optiques grand angulaires non rétrofocus, peuvent être utilisés à une sensibilité de 25 ou 50 ISO, et que cela résout le problème ! En fait l'absence de micro-lentilles fait chuter l'efficacité quantique de détection tout simplement parce que la surface participant effectivement à la collection des photons est beaucoup plus faible qu'avec micro-lentilles.

La solution, nous semble-t-il, est donc dans l'utilisation de pixels plus gros, dont le nombre d'électrons par pixels soit le plus grand possible, captant par leur plus grande surface le plus grand nombre de photons possibles, et dont l'efficacité de détection soit la plus grande possible. C'est facile à dire, mais c'est beaucoup plus difficile à faire si on souhaite que le capteur reste d'un prix abordable.

Un très bon film film diapos couleurs est donc, en termes de bruit et en pratique, à sensibilité ISO équivalente, au moins 4 fois moins bon en rapport signal sur bruit que le capteur silicium, et sans doute cet écart se creuserait-il encore si on pouvait utiliser les capteurs à une plus faible sensibilité, en comptant encore plus d'électrons sans saturer les pixels [6].

Nous tenons certainement là l'une des raisons de la supériorité des images détectées sur silicium, indépendamment des questions de résolution. En plus d'une structure granulaire aléatoire qui existe dans le film indépendamment de toute image, et dont on ne peut pas se débarrasser par interpolation, l'efficacité de détection équivalente n'atteint au maximum que 0,4% pour un film photo courant [9], jusqu'à quelques pourcents [9] pour un film spécial hypersensibilisé ; à comparer aux 20% annoncés par Kodak pour un capteur moyen format récent à matrice colorée Bayer, mais jusqu'à 70% pour un capteur monochrome[10].

Si on ajoute à cela que les photodétecteurs silicium de dimensions millimétriques qu'on peut acheter chez le marchand d'électronique du coin ont des efficacités quantiques de détection qui atteignent 80%, et qu'en capteur d'images de très haut de gamme on atteint aujourd'hui 85% [11], on voit qu'il y a encore une marge de progression pour les capteurs silicium à usage photographique.

Entre un détecteur à 1% d'efficacité équivalente et un détecteur à 20%, le rapport des efficacités est de 20, le gain en rapport signal sur bruit attendu est de √20 soit environ 4 à 5, ceci sans tenir compte de la structure granulaire du film qui de toutes façons restera présente. Alors que la grille d'échantillonnage du capteur, du moins pour les détails pas trop fins et les grands aplats comme les ciels, peut être supprimée grâce à une interpolation bien menée.

Il est regrettable que les dernières recherches sur l'amélioration de la sensibilité et de l'efficacité des films [12] ne donneront sans doute pas lieu à une application pratique. N'oublions pas qu'entre le Kodachrome 25 et la Provia 100F, on a une granularité plus fine et une sensibilité multipliée par 4 ! Mais atteindre aujourd'hui même 10% d'efficacité quantique avec un film semble vraiment hors de portée à la fois techniquement et économiquement.

Conclusion

Au terme de cette longue discussion en deux articles, nos conclusions sont claires, si la détection d'image numérique semble avoir gagné la partie, ce n'est pas seulement une question de décompte de pixels équivalents, c'est aussi, et à terme, surtout une question de bruit, les deux notions participant en parallèle à l'appréciation de la qualité d'une image. Ces conclusions rejoignent celles de Norman Koren [13]

Il y a bien entendu plusieurs objections aux modèles présentés ci-dessus ainsi que dans l'article précédent [2].

La première objection (présentée par M. Dan Fromm, l'un des fidèles lecteurs de galerie-photo résidant aux États-Unis) est la suivante : dans le modèle du facteur 2 à 4 équivalent en surface, pourquoi vouloir absolument numériser le film ? Restons analogiques jusqu'au bout et comparons, in fine, un excellent tirage 100% optique classique avec le résultat d'une numérisation et d'une impression issue du fichier.

Pour ce qui est de l'usage amateur, je suis assez d'accord et je trouve toute satisfaction avec l'agrandissement classique en noir et blanc. Mais le tirage couleur traditionnel à l'agrandisseur est déjà plus délicat à mettre en oeuvre ! La problématique de la numérisation se pose bien évidemment avec acuité aux professionnels dont les clients demandent, exigent même, une livraison sous forme de fichier numérique ; sur ce point il n'est plus guère besoin d'argumenter, le monde de l'édition est très majoritairement numérique, même pour les livres d'art vendus fort chers, et pas seulement les brochures publicitaires qui encombrent votre boîte aux lettres (et contre lesquelles vous n'avez pas encore trouvé de filtre efficace, logiciel ou autre : de plus, certaines vous intéressent peut-être !).

Le passage progressif à la prise de vue numérique s'impose donc pour des raisons économiques et de mise en concurrence entre professionnels. Mais cet argument a un poids bien plus faible pour l'amateur qui, hors du monde concurrentiel, cherche avant tout à pratiquer un loisir manuel et créatif.

La deuxième objection, en particulier présentée par Pascal Miele, est que le modèle ne tient absolument aucun compte du traitement numérique du signal (DSP, digital signal processing) qui est fait dans l'appareil avant la fabrication du fichier auquel l'utilisateur a accès. Sur ce point, sachant qu'on sait depuis les années 1950, par voie analogique-optique, améliorer la netteté d'images floues, connaissant l'exemple illustre de la restauration des images du télescope spatial Hubble avant qu'on ne l'affuble (à grand prix) de verres correcteurs, on se doute bien que la courbe FTM idéalisée du filtre anti-moiré n'est pas laissée telle qu'elle et qu'on essaie de la « remonter » par tous les moyens !

On citera à ce sujet le nouveau format de stockage des données des dos Hasselblad, format permettant, nous dit le fabricant, de corriger les résidus d'aberrations des objectifs a posteriori [14].

On sait également que certains fabricants réalisent un lissage du bruit aux faible niveaux d'éclairement [6] ; ce lissage dégrade la résolution, mais pour des détails de l'image peu visibles ; après tout, on pourrait dire : « pas vu, pas pris » ! Si l'oeil ne le voit pas, pourquoi se priver de tous les traitements d'améliorations possibles ? Mais la lecture des articles de Christian Buil nous prouve que le bruit dans les capteurs à usage photographique grand public n'échappe pas aux bonnes règles du bruit de photons en association avec une efficacité quantique encore limitée pour les matrices de type Bayer, ce qu'on gagnera d'un côté en bruit en combinant des pixels entre eux, on le perdra en résolution.

Enfin une dernière objection, reliée à la précédente, concerne la pertinence de l'analyse FTM, celle des faibles modulations et de la théorie du filtrage linéaire, dans l'évaluation de la qualité visuelle d'une image. Dans le domaine audio, on connaît les traitements non linéaires de type Dolby® qui tiennent compte avec finesse des particularités physiologique de l'oreille humaine ; et pour ce qui est des images, les praticiens du tirage numérique connaissent bien les effets « d'accentuation » si importants pour la qualité visuelle d'un tirage jet d'encre ; le lien entre l'accentuation réalisée sur le fichier et l'analyse en termes de FTM serait à éclaircir.

Le passage du film au capteur numérique a donc été un saut important en termes de bruit, ce qui décale brutalement les formats vers le bas à qualité d'image égale mais qui ne remet pas en cause la hiérarchie des formats. Bien au contraire, le fait que les pixels dans la mission astronomique CoRoT soient de 13 microns et non pas plus petits, nous incite à penser que la diminution de la taille des pixels n'est plus un enjeu maintenant qu'on sait en fabriquer environ 10 millions pour un prix raisonnable.

Rendez-vous est donc pris dans un an ou deux, pour voir si économiquement le capteur 6x8 cm silicium apparaît ou pas sur le marché !

Annexe 1 : Compteur de photons parfait, compteur réel et efficacité du film

Compteur parfait

Un compteur de photons parfait est un dispositif qui transforme chaque photon incident en un signal électronique détectable. Dans les détecteurs photo-électriques utilisés dans le domaine de la lumière visible, chaque photon se transforme en un électron [15]. On va raisonner sur un seul pixel ou sur un seul photodétecteur sans tenir compte de toute la circuiterie nécessaire à repérer où les photons sont tombés. Un compteur parfait fabrique donc un électron pour chaque photon incident, ces électrons devant être mesurés sans pertes.

Si le nombre de photons détectés dans un pixel pendant la pose est en moyenne N₀, on peut montrer qu'il existe des fluctuations naturelles ou bruit de photons sur ce nombre de photons, soit en faisant une deuxième pose identique après remise à zéro du compteur, soit en enregistrant en parallèle un grand nombre de photons tombant dans des détecteurs identiques illuminés par le même éclairement ou le même nombre de photons par unité de surface et par seconde.

Ces fluctuations, appelées écart-type ont comme ordre de grandeur la racine carrée du nombre de photons reçus. Par exemple si la valeur moyenne du signal reçu est 10000 photons, les fluctuations (plus précisément : l'écart-type des fluctuations) sera de l'ordre de 100. Dans ces conditions on a la règle très simple :
 

Compteur photoélectrique idéal, rendement quantique ou efficacité quantique de détection

La perfection n'étant pas de ce monde, il faut nous résoudre à considérer un compteur idéal qui ne diffère du compteur parfait que par sa négligence à compter les photons scrupuleusement. Le compteur est néanmoins idéal car il marque tout de même sur son tableau une certaine fraction des photons incidents, cette fraction qui est caractéristique du compteur est appelée rendement quantique ou efficacité quantique de détection. Pourquoi « quantique » ? tout simplement parce qu'on pense bien entendu à la détection par effet photo-électrique dans laquelle un photon se transforme en un seul électron, effet découvert par Heinrich Hertz en 1887, interprét����������������������������� en termes d'interaction photon-électron par Albert Einstein en 1905 [16].

Le compteur photoélectrique idéal est donc un dispositif qui fabrique et capte une quantité η   N₀ d'électrons chaque fois que N₀ photons sont reçus. La notation consacrée pour ce rendement, qui est la proportion effectivement comptée des photons incidents est η (lettre grecque eta). Un compteur parfait serait caractérisé par une valeur η=100% ; un très bon photomultiplicateur [17] capable de compter les photons un par un a un rendement η =40% ; les détecteurs d'images CCD utilisés en astronomie dépassent 85% [11].

On peut montrer que les fluctuations sur le nombre d'électrons du détecteur idéal sont égales à la racine carrée du nombre d'électrons enregistrés, soit :
 

On voit que le rapport signal sur bruit détecté est d'autant moins bon que le compteur oublie de compter une proportion plus importante de photons. On peut donner une définition générale de l'efficacité quantique de détection équivalente :

 

Pour un compteur de photons idéal de rendement quantique η, l'EQÉ s'identifie à ce rendement.

Pour un film, ou plus généralement pour un détecteur photochimique, l'EQÉ est assez difficile à déterminer hors de l'environnement d'un laboratoire scientifique bien équipé. D'abord il faut définir ce qu'on appelle « signal de sortie », selon qu'on va choisir la densité optique du film ou son facteur de transmission, il y a une petite différence. Ensuite, il y a la structure granulaire propre au film, qui pré-existe indépendamment de toute image donc indépendamment de tout signal, dont on ne peut pas se débarrasser comme on le fait pour la trame d'un capteur d'images silicium. Donc l'extraction de la contribution du bruit de photons au bruit de l'image sur film suppose des conditions opératoires précises permettant de mesurer le rapport signal sur bruit en entrée et en sortie. Clairement une telle étude n'est pas accessible au photographe équipé du matériel de labo-photo classique, On lira à ce sujet le chapitre correspondant du Glafkidès [9], et on sera vite persuadé qu'un capteur silicium à usage photographique est beaucoup plus simple à comprendre en termes de bruit que ce bon vieux film qui nous est si familier ! L'expérience montre qu'on ne peut pas espérer dépasser en EQÉ une valeur de l'ordre du pourcent pour les films photographiques à usage courant.

Le lien entre l'EQÉ d'un film et sa finesse de grain n'est pas direct. On peut par exemple penser à un gélatino-bromure « fait maison » selon les recettes anciennes, qui pourra avoir un grain vraiment très fin (on peut penser à une plaque Lippmann [20], par exemple) mais qui sera un terrible « gâcheur de photons » et dont la sensibilité sera extrêmement faible. Pour un tel film, l'EQÉ sera médiocre.

En revanche un film à grain grossier de très haute sensibilité mais qui compte fidèlement le plus de photons possible pendant un temps de pose très court aura une bien meilleure EQÉ. On peu penser par exemple à certains films instantanés de sensibilité 10000 ISO utilisés autrefois pour la détection en mono-coup des traces d'oscillographes cathodiques.

L'estimation des performances en bruit pour un appareil numérique dont les fichiers RAW sont effectivement accessibles (rien n'oblige en effet les constructeurs à rendre accessibles à l'utilisateur les données premières du nombre d'électrons par pixel !) s'effectue en revanche à l'aide d'un simple logiciel [6].

Annexe 2 : Un modèle binaire pour le film et la loi de Selwyn

Modèle du damier aléatoire

Pour illustrer le compromis qui existe entre le bruit et la résolution, nous proposons de regarder un modèle que nous appellerons damier binaire aléatoire. Pour commencer, nous ne préciserons pas la façon dont ce damier peut être obtenu en pratique, nous chercherons simplement à illustrer le rapport qui existe dans cet objet étrange entre le bruit et la résolution.

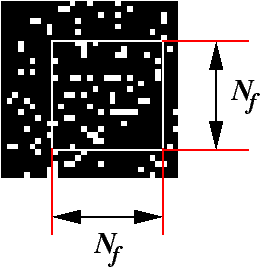
La figure 2 montre une portion agrandie d'un tel damier, l'objet sur lequel nous allons raisonner étant formé de 1000 par 1000 pixels noirs ou blancs. Nous avons choisi de noircir de façon aléatoire l'un ou l'autre des carrés élémentaires du damier, que nous appellerons pixels, avec la règle suivante : il y a 9 chances sur 10 pour que le pixel soit noir, et une chance sur 10 pour qu'il soit blanc.

Figure 2 : Un damier aléatoire pour expliquer les compromis
entre le bruit et la résolution

Si on imprime ce damier d'une façon ou d'une autre sur un support transparent, le facteur de transmission moyen du damier est proche de 10%, en supposant le support bien transparent et en admettant que les noirs sont bien absorbants. Ce facteur de transmission moyen de 10% correspond donc à une densité optique
unité (log₁₀(10) = 1, voir plus bas la définition des densités optiques). En fait dans un tel damier, si on le réalise par un encrage ou par un tirage gélatino-bromure, par une couche mince de gélatine dûment carbonée, ou tout autre procédé, que les noirs soient à une densité de 2 (transmission 1/100) ou de 4 (transmission 1/10000) cela ne change guère la valeur moyenne du facteur de transmission qui sera toujours de l'ordre de 10% dans les deux cas.

On se pose la question de mesurer ce facteur de transmission. On va donc déplacer une fente d'analyse et mesurer la lumière transmise dans une ouverture d'analyse carrée. Si cette fente a une largeur qui correspond à un nombre entier de carrés du damier et qu'on place la fente en coïncidence avec les pixels, le facteur de transmission se déduit facilement du décompte de pixels opaques et du décompte des pixels transparents. Si le nombre total de pixels de la fente est N_f² = N_f × N_f pour une fente de N_f pixels en haut et en large, le facteur de transmission moyen mesuré dans l'ouverture de dimensions N_f par N_f pixels, T_ouv sera simplement égal à :

Figure 3: Définition de l'ouverture d'analyse pour la mesure du facteur de transmission du damier binaire

Par exemple si la fente a un côté de 64 pixels de large, le nombre de pixels analysés sera de 64x64 = 4096, le nombre moyen de pixels blancs sera égal à 10% de ce nombre soit environ 410 pixels.

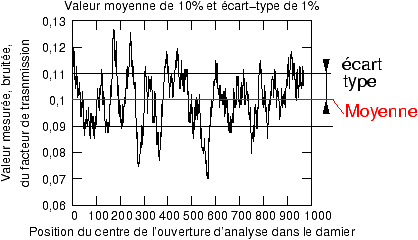
Quel est le bruit ? Bien qu'on ait fait la moyenne sur une ouverture assez large, il reste des fluctuations sur cette mesure lorsqu'on déplace l'ouverture à travers le damier, par exemple la figure 4 montre quelle est l'allure du tracé lorsque l'écart-type des fluctuations sur la mesure est de 1%, autour d'une valeur moyenne du facteur de transmission de 10%. On calcule cet écart-type de façon habituelle en statistiques, si T_mm est par définition la valeur moyenne de toutes les N_m mesures T_i de la quantité T_ouv, T_mm donnée par la formule habituelle pour une moyenne statistique :

on appelle σ_T l'écart-type des fluctuations sur le facteur de transmission T_ouv qui est donné par la formule :

Pour l'estimation de l'écart-type, on divise par (N_m −1) au lieu de N_m pour la moyenne, ceci pour des raisons théoriques un peu longues à justifier ici et de peu d'importance pratique dès que le nombre d'échantillons est élevé. Ces calculs sont accessibles par une simple touche sur toutes les calculettes de poche et dans tous les tableurs, rappelons néanmoins la signification graphique de l'écart-type comme mesure des fluctuations :
 

Figure 4: Moyenne et écart-type d'une mesure de transmission affectée de bruit

Dans ce modèle très simple, le bruit sera donné par les fluctuations sur le nombre de carrés blancs à l'intérieur de la fente d'analyse, soit lorsqu'on analyse un très grand nombre de damiers tous à 10% de transmission moyenne, soit lorsqu'on déplace la fente au-travers un damier donné. Il ne tombe pas sous le sens que les propriétés statistiques soient les mêmes dans les deux types d'analyse, acceptons pour simplifier qu'en balayant la fente à travers le damier et en traçant le facteur de transmission estimé par le décompte de pixels blancs sur la surface de l'ouverture, on a une bonne représentation du bruit. C'est comme cela qu'on procéderait en analysant la granularité d'un film au microdensitomètre. Le lien entre les fluctuations sur le facteur de transmission σ_T et les fluctuations de densité σ_D est donné par :

Au voisinage d'un facteur de transmission de 10%, soit une densité unité, on a donc la correspondance entre fluctuations de densité et fluctuations du facteur de transmission : σ_D(D=1) = 4,3 σ_T(T=0,1). Par exemple lorsque les fluctuations de densité sont de 10 millièmes au voisinage de D=1, les fluctuations absolues du facteur de transmission sont donc de 43 millièmes autour de la valeur T=0,1.

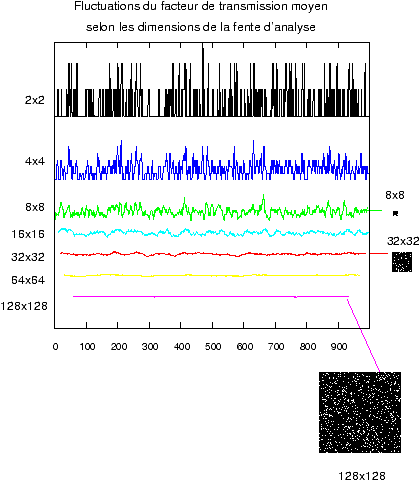
Que donne la simulation sur un damier binaire aléatoire de 1000x1000 pixels, avec 10% de pixels blancs, en fonction de la dimension de la fente d'analyse ? Les résultats de la simulation sont représentés sur la figure 5
 

Figure 5: Plus la fente d'analyse est petite, plus les fluctuations du facteur de transmission sont grandes

On voit que les propriétés statistiques du damier binaire impliquent que plus la fente d'analyse est petite, plus les fluctuations du facteur de transmission sont grandes. Notons bien que ces propriétés du damier n'ont a priori rien à voir avec le bruit de photons, on verra plus bas comment on peut néanmoins relier ce modèle à ce qui se passe dans un film ou un capteur.

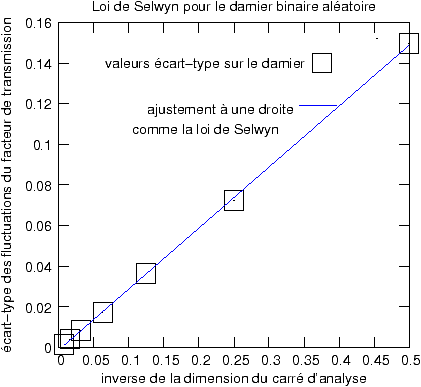
Si on trace en fonction de l'inverse de la dimension du carré d'analyse l'écart-type des fluctuations mesurées, on trouve une relation extrêmement simple (figure 6) :

Figure 6: Les propriétés statistiques d'un damier binaire aléatoire sont analogues à la loi de Selwyn

L'écart-type des fluctuations σ_T sur le facteur de transmission est inversement proportionnel à la largeur de la fente d'analyse, dans notre cas le nombre de pixels de large N_f, ce qu'on peut écrire, en introduisant la surface de l'ouverture N_f × N_f :

Comme les fluctuations de densité autour d'une valeur donnée sont proportionnelles aux fluctuations du facteur de transmission, on aurait, pour ce damier aléatoire, une loi exactement identique, qui est exactement la même que la Loi de Selwyn pour les films.

Loi de Selwyn et bruit de granularité du film

Principe du densitomètre et du micro-densitomètre

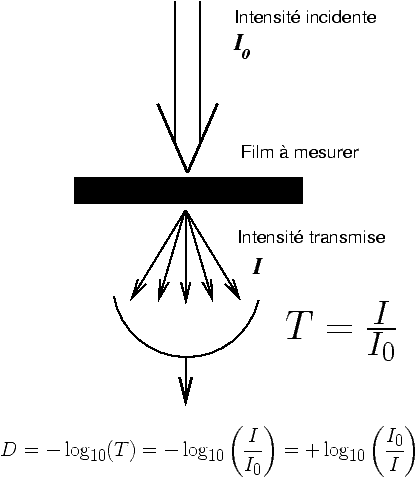
Pour faire le lien entre le modèle précédent et ce qui se passe réellement dans un film, nous rappellerons les principes de mesure du facteur de transmission ou de la densité optique d'un film. Dans un densitomètre (figure 7), on compare le flux lumineux I transmis à travers une certaine plage absorbante du film avec une valeur de référence I₀, le plus souvent mesurée sur la partie non exposée du film. Cette partie n'est cependant pas totalement transparente, le facteur de transmission mesuré en référence correspond à la transmission maximale du support et du voile du film.
 

Figure 7: Principe du densitomètre en transmission

Le facteur de transmission T est défini par :

Si le film ne transmet que 10% de la lumière, son facteur de transmission sera donc égal à 0,1. On définit la densité optique D par la relation :

À un facteur de transmission de 0,1 correspond donc une densité optique de 1, le tableau ci-dessous rappelle la correspondance entre facteur de transmission, densité optique, coefficient prolongateur de pose et crans de diaphragme pour différents cas usuels.

 

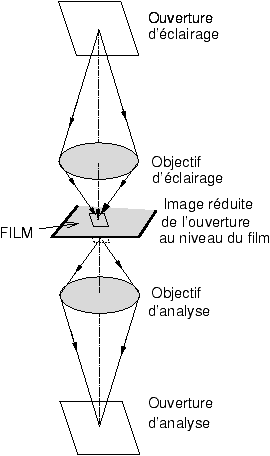
Les densitomètres usuels utilisés pour le tirage ont de dimensions de fente d'analyse de l'ordre du millimètre, ils permettent de mesurer la valeur moyenne de la densité sur une plage qui peut être sélectionnée avec précision, mais ils ne permettent pas de mesurer les fluctuations de granularité. Pour cela il faut utiliser un appareil appelé micro-densitomètre, qui ne diffère du densitomètre que par sa capacité à utiliser des fentes d'analyse très fines, jusqu'à 5x5 microns. Pour cela on procède par projection sur le film d'une première ouverture, l'ouverture d'éclairage à l'aide d'un premier objectif de microscope et on fait l'image de la partie éclairée du film en transmission à l'aide d'un deuxième objectif identique au premier, suivi d'une fente d'analyse de dimensions voisines de la fente d'éclairage.
 

Figure 8: Principe du micro-densitomètre à fentes conjuguées pour la mesure de la granularité des films

La loi de Selwyn, proposée en 1935[21] relie les fluctuations de densité σ_D mesurées au microdensitomètre avec la surface ou aire A de la fente d'analyse, quelle que soit sa forme [22] :
 

Cette loi empirique qui a exactement la même forme que la loi trouvée pour le damier binaire aléatoire est à la base de la définition de la granularité RMS [18]. RMS veut dire « root mean square » c'est à dire écart quadratique moyen. La granularité s'exprime en millièmes de fluctuations au voisinage d'une densité unité, pour une ouverture d'analyse circulaire de diamètre 48 microns. Le coefficient de Selwyn G est caractéristique du film, mais il dépend un peu de la forme de l'ouverture (carrée ou circulaire) ainsi que des conditions d'éclairage.

Il est remarquable que cette loi corresponde à ce que donnerait un damier aléatoire, mais il est également remarquable que la loi serait la même pour un détecteur de photons idéal sans bruit propre, dans lequel on compte les électrons qui sont reçus dans une certaine surface. Il suffit par exemple d'imaginer que les points blancs du damier de la figure 2 représentent le point d'impact des électrons pendant un temps de pose donné, en prenant par exemple une cellule de 200 par 200 cases pour l'analyse on aurait une assez bonne image de la distribution statistique dans un capteur dont les pixels peuvent compter jusqu'à 200x200=40000 électrons. Chaque fois qu'on réduit la surface d'analyse d'un facteur 4, le rapport signal sur bruit se dégrade d'un facteur 2 pour un même nombre moyen d'électrons reçus par unité de surface. Inversement, grouper les cases entre elles permet de lisser le bruit au prix d'une perte de résolution.

Pourquoi il est parfois illusoire de « scanner plus fin »

Cette loi de Selwyn s'applique assez bien aux films noir et blanc classiques positif ou négatifs, à grains traditionnels ou à grains plats, elle s'applique assez bien aux films pour diapositives couleurs, mais son application aux films négatifs couleur les plus modernes est devenue sujette à caution tellement le bruit de granularité est faible dans ces supports dépourvus d'argent après développement.

La loi de Selwyn permet néanmoins d'expliquer un certain nombre d'observations photographiques courantes, en particulier l'avantage du grand format en termes de bruit et de différenciation des niveaux de gris. De façon plus quantitative, elle nous permet d'espérer moins de bruit de granularité dans l'analyse d'un film on fait la moyenne sur de plus gros éléments d'image. C'est ce qu'on fait en préférant le grand format sur film plutôt que le petit format avec le même film, on peut même dire que pour un même film, numériser le film avec une fente 4 fois plus large en surface doit en principe améliorer le rapport signal sur bruit d'un facteur 2 au détriment de la résolution. Ce qui nous ramène à la question du nombre maximum de pixels équivalents lorsqu'on numérise un film. L'éclairage dans un scanner n'est pas exactement celui d'un microdensitomètre, mais il serait étonnant qu'une loi analogue à celle de Selwyn ne s'applique pas. Il est donc illusoire de vouloir scanner trop finement, même si l'optique du scanner est excellente et la mise au point et tenue du film sont parfaites, à cause de l'amplification du bruit qui est la conséquence de l'effet de moyenne statistique des mesures de densité sur de très petites ouvertures.

On dit en général qu'au-delà d'un certain nombre de points par pouce, « on ne scanne plus que du grain » cette expression imagée prend donc son sens en disant que plus on scanne fin, plus l'écart-type de fluctuations augmente, et que si on veut lisser ces fluctuations, on doit s'arrêter à ce qui donnera le meilleur compromis entre le bruit et la résolution.

Entendons-nous bien : il faut déjà disposer d'un scanner de qualité professionnelle pour que la qualité des images ne soit pas limitée par la médiocre performance optique et mécanique du scanner, mais lorsque l'appareil est bon, on va buter sur les limites imposées par ces fluctuations de granularité. En d'autres termes, scanner deux fois plus fin dans les deux directions multiplie le bruit par deux, cela ne sert à rien s'il faut ensuite recombiner 4 pixels pour lisser ce bruit et obtenir une image acceptable.

Annexe 3 : Comparaison de bruit entre la Provia 100F et le Canon EOS 5D en conditions photographiques usuelles

Prenons par comparaison un excellent film comme la Provia 100F avec une granularité RMS de 8, ceci veut dire que dans une ouverture circulaire de 48 microns (même surface qu'un carré de 42 microns de côté) au voisinage de la densité unité, les fluctuations de densité dD sont de 8 millièmes. Si on analysait le film avec la même surface que le pixel de 8,2 microns de côté de l'EOS 5D, on devrait s'attendre à une multiplication des fluctuations de granularité dans le rapport des largeurs des ouvertures d'analyse (loi de Selwyn), fente ou pixel, soit environ 5x entre 8,2 et 42 microns (racine carrée du rapport des surfaces, rapport des côtés des carrés), le bruit de granularité en densité dD serait donc de l'ordre de 40 millièmes ramené à 8,2 microns d'ouverture.

Pour comparer avec le capteur silicium dont les mesures de bruit sont exprimées en nombre d'électrons ou en pas du codeur analogique/numérique, avant tout il faut transformer ces fluctuations de densité (échelle logarithmique) en fluctuations de lumination équivalente lors de l'exposition du film (une échelle linéaire, comme un nombre de photons reçus).

Si on se place dans la partie rectiligne de la courbe caractéristique (densités/log des luminations) du film, on a la relation classique :
 

où dD désigne les variations de densité, γ selon la notation consacrée la pente de la courbe caractéristique de noircissement dans sa partie rectiligne, L la lumination (le terme 0,43 = 1/2,3 vient du logarithme décimal). Pour une diapositive (inversible), la pente est négative, et pour le film diapositives Provia 100F le gamma est de l'ordre de 1,66, 1,66×0,43 = 0,7. On obtient finalement avec ce gamma de 1,66 :
dD = γ d(Log₁₀( L))= 0,7   d L/ L.

Dans ces conditions, une valeur de fluctuation dD de 40 millièmes en densité correspond à une fluctuation relative de lumination dL/L de 40/0,70 = 57 millièmes environ. Si on considère que la grandeur de sortie intéressante est la densité, le rapport signal sur bruit exprimé en densité serait donc de 1000/40 = 25. Si au contraire on veut se représenter le film comme un détecteur d'éclairement lumineux, et le comparer au capteur silicium avant traitement logiciel, il faut se référer aux fluctuations équivalentes de lumination en échelles linéaires à l'entrée, avant cette conversion logarithmique des densités soit 1000/57 = 17,5 environ.

Le rapport signal sur bruit dans les capteurs est en fait nettement meilleur que cela, pas 10 fois meilleur mais 2 fois meilleur si on se réfère à l'EOS 5D à 400 ISO ; il faudrait cependant comparer la même sensibilité ISO équivalente. Christian Buil [6] trouve en pratique avec le Canon EOS 5D réglé sur 400 ISO, un rapport signal sur bruit de 34,6 en échelle linéaire à l'entrée lorsque le niveau de signal est 7,5% de la saturation (308 pas de codeurs pour un total maximum de 4095 = 12 bits, valeur qui n'est pas toujours atteinte d'ailleurs).

Avec un signal correspondant à 10% de la saturation pour se mettre à peu près dans les mêmes conditions que la Provia 100 F (avec une densité de 1, on peut encore multiplier la lumination par 10 avant d'atteindre le « grillage » définitif des blancs de la Provia), on trouverait un rapport signal sur bruit de l'ordre de 40. Alors que la Provia 100F n'a que 100 ISO de sensibilité, qu'elle demande donc 4 fois plus de photons par unité de surface par comparaison avec un 400 ISO. Si on extrapole le bruit du capteur toujours à 10% de la saturation mais avec un réglage de 100 ISO, cela veut simplement dire en supposant que le pixel n'est pas saturé qu'on va recevoir 4 fois plus de photons en entrée, donc on aura 4 fois plus d'électrons dans le signal stocké par pixel, pour une réduction des fluctuations relatives d'un facteur √4=2 par rapport au réglage 400 ISO. On s'attend donc à un facteur 4 en signal sur bruit en faveur de l'EOS 5D par rapport à la Provia 100F utilisée à la même sensibilité de 100 ISO.

Il y a une très bonne fiche technique Fuji, voir à la fin du document, qui résume la définition de la FTM d'un film et de la granularité RMS [18].

Annexe 4 : Estimation du nombre de photons tombant sur un pixel de capteur

On pourrait penser que le photon n'est accessible qu'à des expériences de physique très précises où on va détecter de très faibles flux, par exemple avec un photomultiplicateur. En grâce réalité l'analyse du bruit dans un appareil photo grand public, en comparant les résultats avec un capteur professionnel dont l'efficacité quantique est donnée, on peut estimer assez simplement le nombre de photons incidents sur un pixel. Par exemple C. Buil [6] estime à 5% l'efficacité quantique de détection dans le vert pour le capteur de l'EOS 5D. En parallèle, avec un signal d'entrée qui correspondrait à peu pr��s à la moitié de l'échelle de sortie jpeg (niveau 128 sur 255), on estime une valeur d'environ 1200 électrons détectés pour atteindre ce niveau. Les fluctuations naturelles du nombre d'électrons sont à peu près √1200 soit 34,6, pour un rapport signal sur bruit identique. Avec un rendement de 5% le nombre de photons incidents est donc de 32000. Si le détecteur avait un rendement de 70% comme les détecteurs d'images monochromes, avec le même nombre de photons incidents le nombre d'électrons détectés serait de 22000, le rapport signal sur bruit serait de l'ordre de √22000 ≃ 150. En repartant sur le capteur avec un rendement de 5% mais en utilisant le réglage 100 ISO et en supposant qu'on n'atteint pas la saturation, le gain en signal/bruit par rapport au réglage 400 ISO est un facteur 2, soit une valeur estimée à environ 70.

Il est très remarquable, selon C. Buil [6], que les différents bruits électroniques qui s'ajoutent à ce bruit de photons (induisant le bruit de signal sur le nombre d'électrons détectés) soient quasi indiscernables en usage photographique ordinaire. En-dessous de 5 minutes de pose, le bruit thermique reste difficilement perceptible, et dès que la sensibilité ISO est réglée à 1000 ISO ou moins (pour l'EOS 5D), la limite de bruit total, bien entendu dans la limite de la non-saturation du pixel, est donnée par le bruit de photons et l'efficacité quantique de détection.

Références

Emmanuel Bigler 18 mai 2007

Télécharger l'article au format pdf.

dernière modification de cet article : 2007